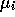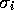The agents choose cars according to their "internal representation" of the characteristics of the products. These internal representations are probability distributions of the utility of each product that are computed according to the following procedure.
- Agents access some public information about the performance of each
brand i,
represented by a normal prior probability distribution ,
with mean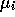 
and
standard deviation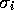 
.
- They take advice from n other purchasers, among which
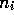bought
brand i. Only those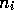 
purchaser that bought brand i
contribute to the information about brand i
by sending a measure of its utility:
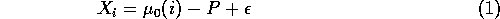
where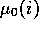 
is the average utility of brand i in the absence of pollution.
Since the sampled purchasers already possess
the brand, their opinion about the brand includes the negative
effects of pollution. We suppose here that they don't know
the origin of pollution, in such a way
that the decrease in the car utility is proportional
to local pollution, irrespective of which brand they have purchased
themselves. Utility is then decreased by the presence of pollution
P expressed in the convenient cost units.
, representing measurement error,
is a normally distributed random variable, but with mean 0 and
standard deviation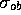 
invariant through the
iteration process.
The agents process this information to obtain a posterior
distribution of performances. This processing is done by taking
the convolution products of Gaussian integrals corresponding to
the prior and to the information obtained from other purchasers.
The average expected posterior utility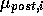 
is then:
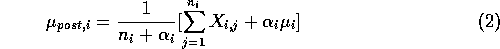
where index j refers to the pooled agent. The mean utilities are averaged with a weighting factor that is inversely proportional to the variance of the distribution:
In other words the posterior utilities average the different polled opinions weighted inversely to the variance of the distributions. The computation of posterior is illustrated for a particular case on figure 1.
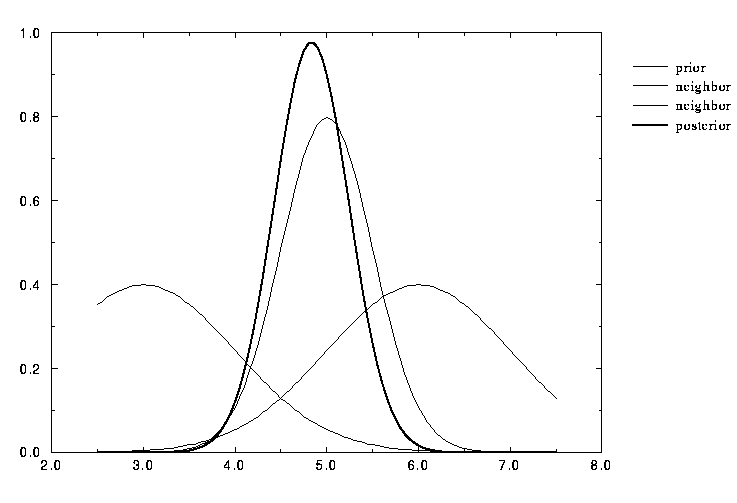
Figure 1: An example of updating the internal representation
of an agent according to equations 2 and 3.
The prior distribution of utilities for a given brand,
with mean 5 and standard deviation 0.5 (intermediate linewidth Gaussian)
is updated to the posterior distribution with mean 4.83 and
standard deviation 0.41
(larger linewidth Gaussian) after taking into account information obtained
from neighbors with means 3 and 6 and standard deviation
2 (smaller linewidth Gaussians).
In this example, the posterior distribution is shifted
and sharpened with respect to the prior.
Economic agents are adverse to risk. The greater the uncertainty in
the value of a product, the less they are likely to buy it.
To take into account risk aversion of the agents,
we use a classical
mean variance utility function:
one more term, proportional to the variance of
the posterior distribution, is added to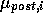 
to compute the effective utility function
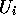used by the agents to choose their car:
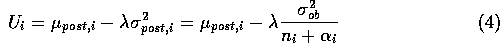
where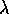 
is the risk aversion parameter and
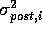is updated by narrowing the
variance according to the number of sampled purchasers.
The complete expression for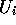 
is then:
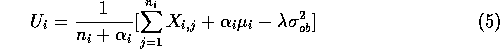
Upon computing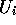 
for each product,
purchasers choose the brand with the highest expected utility.