


Next: SIMULATION RESULTS
Up: THE MODEL
Previous: Pollution dynamics
Every time the agent is facing a new choice, he polls his neighbors
and gets some information. This succession of information can be used in different ways.
One way is to forget the information obtained at previous time steps
and recompute at the next time step
the utility function from the same initial priors.
In this case the priors are not updated.
Another possibility is to memorize all the information
acquired at each time step by using as priors for
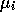 ,
, 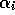 and
and 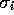 the posteriors
derived from equation 2 at the previous time step.
We call this choice maximum updating.
But
the posteriors
derived from equation 2 at the previous time step.
We call this choice maximum updating.
But 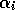 increases in time as the total number of
polled opinions. The importance of the risk aversion parameter
is then rapidly decreasing. Furthermore,
agents using maximum updating would give the same importance
to old and new information and would tend to be overconfident
because the variance of the utility probability distribution
is constantly decreased. An image of such an agent would
be an obstinate old man that does not care any more about the present situation
and refers only to the old times. Maximum updating is thus fairly
insensitive to the variable changes in time and
does not fit well with dynamical processes.
increases in time as the total number of
polled opinions. The importance of the risk aversion parameter
is then rapidly decreasing. Furthermore,
agents using maximum updating would give the same importance
to old and new information and would tend to be overconfident
because the variance of the utility probability distribution
is constantly decreased. An image of such an agent would
be an obstinate old man that does not care any more about the present situation
and refers only to the old times. Maximum updating is thus fairly
insensitive to the variable changes in time and
does not fit well with dynamical processes.
An intermediate possibility is to decrease the relative importance
of older information. This is simply achieved by limiting the 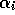 to a maximum value of
to a maximum value of 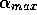 . To see why
choosing an
. To see why
choosing an 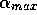 is equivalent to a short term memory,
let us suppose that several iterations have been made with
is equivalent to a short term memory,
let us suppose that several iterations have been made with
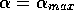 , in a neighborhood where the fraction
, in a neighborhood where the fraction 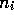 of purchasers have not changed.
By iterating the utility expression (2) towards the past one obtains:
of purchasers have not changed.
By iterating the utility expression (2) towards the past one obtains:
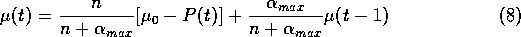
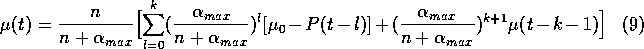
where l is the time difference between the past step and the present.
Utilities from the past are then
discounted by a factor 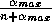 at each time step, and since
at each time step, and since 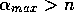 ,
this corresponds to a decay time for memory of
,
this corresponds to a decay time for memory of
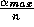 . In other words limiting
. In other words limiting 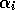 to
to
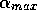 is somehow equivalent to limit the averaging process to the
is somehow equivalent to limit the averaging process to the
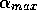 most recent information.
most recent information.
The prior updating process is only performed on the internal
representation of the agents. It does not apply to the information
transmitted between the agents, when the main source
of uncertainty is the polling process itself. In equation 1,
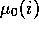 always represent the initial average utility
of brand i. It is, of course, a constant of the simulation.
always represent the initial average utility
of brand i. It is, of course, a constant of the simulation.



Next: SIMULATION RESULTS
Up: THE MODEL
Previous: Pollution dynamics
weisbuch
Tue Feb 4 16:55:42 GMT+0100 1997
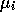 ,
, 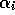 and
and 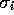 the posteriors
derived from equation 2 at the previous time step.
We call this choice maximum updating.
But
the posteriors
derived from equation 2 at the previous time step.
We call this choice maximum updating.
But 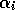 increases in time as the total number of
polled opinions. The importance of the risk aversion parameter
is then rapidly decreasing. Furthermore,
agents using maximum updating would give the same importance
to old and new information and would tend to be overconfident
because the variance of the utility probability distribution
is constantly decreased. An image of such an agent would
be an obstinate old man that does not care any more about the present situation
and refers only to the old times. Maximum updating is thus fairly
insensitive to the variable changes in time and
does not fit well with dynamical processes.
increases in time as the total number of
polled opinions. The importance of the risk aversion parameter
is then rapidly decreasing. Furthermore,
agents using maximum updating would give the same importance
to old and new information and would tend to be overconfident
because the variance of the utility probability distribution
is constantly decreased. An image of such an agent would
be an obstinate old man that does not care any more about the present situation
and refers only to the old times. Maximum updating is thus fairly
insensitive to the variable changes in time and
does not fit well with dynamical processes.
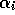 to a maximum value of
to a maximum value of 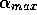 . To see why
choosing an
. To see why
choosing an 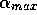 is equivalent to a short term memory,
let us suppose that several iterations have been made with
is equivalent to a short term memory,
let us suppose that several iterations have been made with
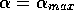 , in a neighborhood where the fraction
, in a neighborhood where the fraction 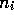 of purchasers have not changed.
By iterating the utility expression (2) towards the past one obtains:
of purchasers have not changed.
By iterating the utility expression (2) towards the past one obtains:
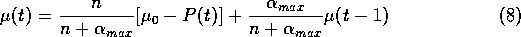
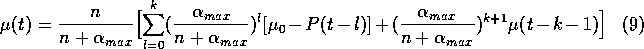
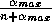 at each time step, and since
at each time step, and since 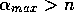 ,
this corresponds to a decay time for memory of
,
this corresponds to a decay time for memory of
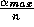 . In other words limiting
. In other words limiting 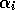 to
to
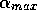 is somehow equivalent to limit the averaging process to the
is somehow equivalent to limit the averaging process to the
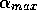 most recent information.
most recent information.
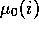 always represent the initial average utility
of brand i. It is, of course, a constant of the simulation.
always represent the initial average utility
of brand i. It is, of course, a constant of the simulation.