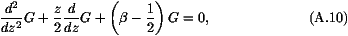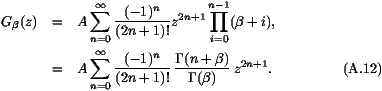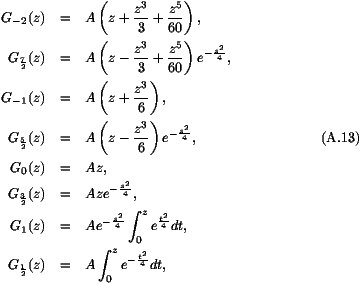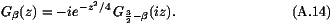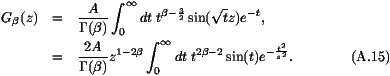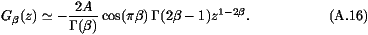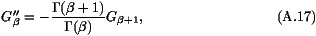Shift in the velocity of a front due to a cut-off
Abstract:
We consider the effect of a small cut-off  on the velocity
of a traveling wave in one dimension. Simulations done over more than ten
orders of magnitude as well as a simple theoretical argument indicate
that the effect of the cut-off
on the velocity
of a traveling wave in one dimension. Simulations done over more than ten
orders of magnitude as well as a simple theoretical argument indicate
that the effect of the cut-off  is to select a single velocity
which converges when
is to select a single velocity
which converges when 
 0 to the one predicted by the marginal
stability argument. For small
0 to the one predicted by the marginal
stability argument. For small  , the shift in velocity has the
form K(log
, the shift in velocity has the
form K(log )-2 and our prediction for the constant K
agrees very well with the results of our simulations. A very similar
logarithmic shift appears in more complicated situations, in particular in
finite size effects of some microscopic stochastic systems. Our
theoretical approach can also be extended to give a simple way of
deriving the shift in position due to initial conditions in the
Fisher-Kolmogorov or similar equations.
)-2 and our prediction for the constant K
agrees very well with the results of our simulations. A very similar
logarithmic shift appears in more complicated situations, in particular in
finite size effects of some microscopic stochastic systems. Our
theoretical approach can also be extended to give a simple way of
deriving the shift in position due to initial conditions in the
Fisher-Kolmogorov or similar equations.
02.50.Ey, 03.40.Kf, 47.20.Ky
1 Introduction
Equations describing the propagation of a front between a stable and an
unstable state appear [1, 2, 3, 4, 5, 6, 7] in a large variety of situations in
physics, chemistry and biology. One of the simplest equations of this
kind is the Fisher-Kolmogorov [1, 2]
equation
which describes the evolution of a space and time dependent concentration
h(x,t) in a reaction-diffusion system. This equation, originally
introduced to study the spread of advantageous genes in a
population [1], has been widely used in other contexts, in
particular to describe the time dependence of the concentration of some
species in a chemical reaction [8, 9].
For such an equation, the uniform solutions h=1 and h=0 are
respectively stable and unstable and it is known [3, 7, 10, 11, 12] that for initial conditions such that
h(x,0)  1 as x
1 as x  -
- and h(x,0)
and h(x,0)  0 as x
0 as x  +
+
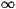 there exists a one parameter family Fv of traveling wave
solutions (indexed by their velocity v) of the form
there exists a one parameter family Fv of traveling wave
solutions (indexed by their velocity v) of the form
with Fv decreasing, Fv(z)  1 as z
1 as z  -
- 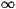 and Fv(z)
and Fv(z)
 0 as z
0 as z 
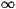 . The analytic expression of the shape Fv is
in general not known but one can determine the range of velocities v for
which solutions of type (2) exist. If one assumes an
exponential decay
. The analytic expression of the shape Fv is
in general not known but one can determine the range of velocities v for
which solutions of type (2) exist. If one assumes an
exponential decay
it is easy to see by replacing (2) and (3) into
(1) that the velocity v is given by
As  is arbitrary, this shows the well known fact that the
range of possible velocities is v
is arbitrary, this shows the well known fact that the
range of possible velocities is v 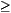 2. The minimal velocity v0=2
is reached for
2. The minimal velocity v0=2
is reached for  0=1 and for steep enough initial conditions
h(x,0) (which decay faster than e-
0=1 and for steep enough initial conditions
h(x,0) (which decay faster than e- 0 x), the solution
selected [3, 4, 6, 7, 10, 11, 12] for large t
is the one corresponding to this minimal velocity v0.
0 x), the solution
selected [3, 4, 6, 7, 10, 11, 12] for large t
is the one corresponding to this minimal velocity v0.
Equations of type (1) are obtained either as the large
scale limit [5, 8, 13, 14, 15, 16] or as the mean field
limit [17] of physical situations which are
discrete at the microscopic level (particles, lattice models, etc.) As
the number of particles is an integer, the concentration h(x,t) could
be thought as being larger than some  , which would correspond
to the value of h(x,t) when a single particle is present. Equations of
type (1) appear then as the limit of the discrete model when
, which would correspond
to the value of h(x,t) when a single particle is present. Equations of
type (1) appear then as the limit of the discrete model when

 0. Several authors [8, 13, 14] have already
noticed in their numerical works that the speed v
0. Several authors [8, 13, 14] have already
noticed in their numerical works that the speed v of the
discrete model converges slowly, as
of the
discrete model converges slowly, as  tends to 0, towards the
minimal velocity v0. We believe that the main effect of having
tends to 0, towards the
minimal velocity v0. We believe that the main effect of having

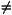 0 is to introduce a cut-off in the tail of the front, and
that this changes noticeably the speed.
0 is to introduce a cut-off in the tail of the front, and
that this changes noticeably the speed.
The speed of the front is in general governed by its tail. In the
present work, we consider equations similar to (1), which we
modify in such a way that whenever h(x,t) is much smaller than a
cut-off  , it is replaced by 0. The cut-off
, it is replaced by 0. The cut-off  can be
introduced by replacing (1) by
can be
introduced by replacing (1) by
with
For example, one could choose a(h)=1 for h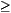
 and
a(h)=h/
and
a(h)=h/ for h
for h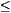
 . Another choice that we will use in
section iv is simply a(h)=1 if h>
. Another choice that we will use in
section iv is simply a(h)=1 if h> and a(h)=0
if h
and a(h)=0
if h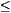
 .
.
The question we address here is the effect of the cut-off  on the velocity v
on the velocity v of the front. We will show that the velocity
v
of the front. We will show that the velocity
v converges, as
converges, as 
 0, to the minimal velocity
v0 of the original problem (without cut-off) and that the main
correction to the velocity of the front is
0, to the minimal velocity
v0 of the original problem (without cut-off) and that the main
correction to the velocity of the front is
for an equation of type (1) for which the velocity is
related to the exponential decay  of the shape (2)
by some relation v(
of the shape (2)
by some relation v( ). (Everywhere we note by v0 the minimal
velocity and
). (Everywhere we note by v0 the minimal
velocity and  0 the corresponding value of the decay
0 the corresponding value of the decay  .)
In the particular case of equation (1), where v(
.)
In the particular case of equation (1), where v( ) is
given by (4), this becomes
) is
given by (4), this becomes
In section ii we describe an equation of
type (1) where both space and time are discrete, so that
simulations are much easier to perform. The results of the numerical
simulations of this equation are described in section iii:
as 
 0, the velocity is seen to converge like
(log
0, the velocity is seen to converge like
(log )-2 to the minimal velocity v0, and the
shape of the front appears to take a scaling form.
)-2 to the minimal velocity v0, and the
shape of the front appears to take a scaling form.
In section iv we show that for equations of
type (1) in presence of a small cut-off  as
in (5), one can calculate both the shape of the front and
the shift in velocity. The results are in excellent agreement with the
numerical data of section iii.
as
in (5), one can calculate both the shape of the front and
the shift in velocity. The results are in excellent agreement with the
numerical data of section iii.
In section v we consider a model defined, for a finite
number N of particles, by some microscopic stochastic dynamics which
reduces to the front equation of sections iii
and iv in the limit N
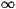 . Despite the presence of
noise, our simulations indicate that in this case too, the velocity
dependence of the front decays slowly (as (log N)-2) to
the minimal velocity v0 of the front.
. Despite the presence of
noise, our simulations indicate that in this case too, the velocity
dependence of the front decays slowly (as (log N)-2) to
the minimal velocity v0 of the front.
2 A discrete front equation
To perform numerical simulations, it is much easier to study a case
where both time and space are discrete variables. We consider here the
equation
where
Time is a discrete variable and if initially the concentration
h(x,0) is only defined when x is an integer, h(x,t) remains so at
any later time. Because t and x are both integers, the cut-off
 can be introduced as in (9) in the crudest way
using a Heaviside Theta function. (We have checked however that other
ways of introducing the cut-off
can be introduced as in (9) in the crudest way
using a Heaviside Theta function. (We have checked however that other
ways of introducing the cut-off  as in (5,
6) do not change the results.)
as in (5,
6) do not change the results.)
Equation (9) appears naturally (in the limit
 =0) in the problem of directed polymers on disordered
trees [17, 18] (where the
energy of the bonds is either 1 with probability p or 0 with
probability 1-p). At this stage we will not give a justification for
introducing the cut-off
=0) in the problem of directed polymers on disordered
trees [17, 18] (where the
energy of the bonds is either 1 with probability p or 0 with
probability 1-p). At this stage we will not give a justification for
introducing the cut-off  . This will be discussed in
section v.
. This will be discussed in
section v.
We consider for the initial condition a step function
Clearly for such an initial condition, h(x,t)=1 for x < 0 at all
times. As h(x,t)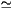 1 behind the front and h(x,t)
1 behind the front and h(x,t)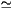 0 ahead of the
front, we define the position Xt of the front at time t by
0 ahead of the
front, we define the position Xt of the front at time t by
The velocity of the front v can then be calculated by
can then be calculated by
where the average is taken over time. (Note that as h(x,t) is only
defined on integers, the difference Xt+1-Xt is time dependent and
has to be averaged as in (12).)
When  =0, the evolution equation (9) becomes
=0, the evolution equation (9) becomes
As for (1), there is a one parameter family of solutions
Fv of the form (2) indexed by the velocity v which is
related (3) to the exponential decay  of the shape by
of the shape by
(This relation is obtained as (4) by considering the tail of
the front where h(x,t) is small and where therefore (13) can be
linearized.)
One can show that for p<1/2, v( ) reaches a minimal
value v0 smaller than 1 for some
) reaches a minimal
value v0 smaller than 1 for some  0, whereas for
p
0, whereas for
p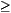 1/2, v(
1/2, v( ) is a strictly decreasing function of
) is a strictly decreasing function of
 , implying that the minimal velocity is v0=
lim
, implying that the minimal velocity is v0=
lim

 v(
v( )=1.
)=1.
We will not discuss here this phase transition and we assume from now
on that p<1/2. Table i gives some values of v0
and  0 obtained from (14).
0 obtained from (14).
| p |
0.05 |
0.25 |
0.45 |
|
 0 0 |
2.751 111... |
2.553 244... |
4.051 851... |
| v0 |
0.451 818... |
0.810 710... |
0.979 187... |
Table 1: Values of
 0
0 and
v0 for some
p when

=0.
It is important to notice that for p<1/2, the
function v( ) has a single minimum at
) has a single minimum at  0. Therefore, there
are in general two choices
0. Therefore, there
are in general two choices  1 and
1 and  2 of
2 of  for each
velocity v. For v
for each
velocity v. For v v0, the exponential decay of Fv(z) is dominated by
min(
v0, the exponential decay of Fv(z) is dominated by
min( 1,
1, 2). As v
2). As v  v0, the two roots
v0, the two roots  1 and
1 and
 2 become equal, and the effect of this degeneracy gives (in
a well chosen frame)
2 become equal, and the effect of this degeneracy gives (in
a well chosen frame)
where A is a constant. This large z behavior can be recovered by
looking at the general solution of the linearized form of
equation (13)
3 Numerical determination of the velocity
We iterated numerically (9) with the initial condition
(10) for several choices of p < 1/2 and for
 varying between 0.03 and 10-17. We observed that the
speed is usually very easy to measure because, after a short transient
time, the system reaches a periodic regime for which
varying between 0.03 and 10-17. We observed that the
speed is usually very easy to measure because, after a short transient
time, the system reaches a periodic regime for which
for some constants T and Y. The speed v of the front is
then simply given by
of the front is
then simply given by
For example, for p=0.25 and  =10-5, we find T=431 and
Y=343 so that v
=10-5, we find T=431 and
Y=343 so that v =343/431. The emergence of this periodic
behavior is due to the locking of the dynamical system of the h(x,t) on
a limit cycle. Because Y and T are integers, our numerical
simulations give the speed with an infinite accuracy.
=343/431. The emergence of this periodic
behavior is due to the locking of the dynamical system of the h(x,t) on
a limit cycle. Because Y and T are integers, our numerical
simulations give the speed with an infinite accuracy.
For each choice of p and  , we measured the speed of the
front, as defined by (12) and its shape.
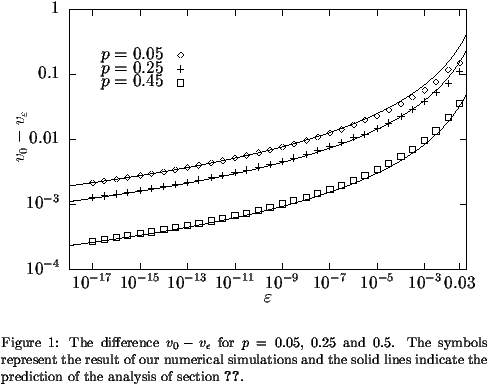
Figure 1 is a log-log plot of the difference v0-v
, we measured the speed of the
front, as defined by (12) and its shape.
Figure 1 is a log-log plot of the difference v0-v versus
versus  (varying between 0.03 to 10-17) for three
choices of the parameter p. The solid lines on the plot indicate the
value predicted by the calculations of section iv.
(varying between 0.03 to 10-17) for three
choices of the parameter p. The solid lines on the plot indicate the
value predicted by the calculations of section iv.
We see on this figure that the velocity v converges
slowly towards the minimal velocity v0 as
converges
slowly towards the minimal velocity v0 as 
 0. Our
simulations, done over several orders of magnitude (here, fifteen),
reveal that the convergence is logarithmic: v0 - v
0. Our
simulations, done over several orders of magnitude (here, fifteen),
reveal that the convergence is logarithmic: v0 - v ~
(log
~
(log )-2.
)-2.
As the front is moving, to measure its shape, we need to locate its
position. Here we use expression (11) and we measure the
shape s (z) of the front at a given time t relative to its
position Xt by
(z) of the front at a given time t relative to its
position Xt by
When the system reaches the limit cycle (17), the shape
s (z) becomes roughly independent of the time chosen. (In fact
it becomes periodic of period T, but the shape s
(z) becomes roughly independent of the time chosen. (In fact
it becomes periodic of period T, but the shape s has a
smooth envelope.) We have measured this shape at some arbitrary large
enough time to avoid transient effects. As we expect s
has a
smooth envelope.) We have measured this shape at some arbitrary large
enough time to avoid transient effects. As we expect s (z) to
look more and more like Fv0(z) as
(z) to
look more and more like Fv0(z) as  tends to 0, we
normalize this shape by dividing it by e-
tends to 0, we
normalize this shape by dividing it by e- 0z. The result
s
0z. The result
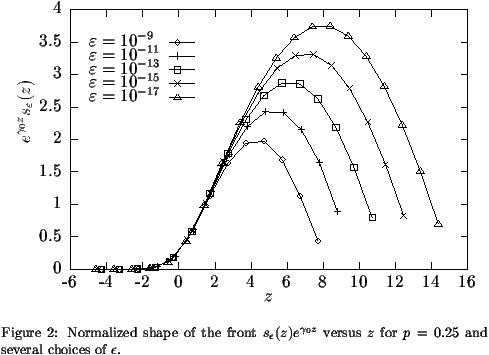
s (z) e
(z) e 0z is plotted versus z for p=0.25 and
0z is plotted versus z for p=0.25 and
 =10-9, 10-11, 10-13, 10-15 and 10-17 in
figure 2.
=10-9, 10-11, 10-13, 10-15 and 10-17 in
figure 2.
On the left part of the graph, our data coincide over an increasing
range as  decreases, indicating that far from the cut-off, the
shape converges to expression (15) of
Fv0(z). On the right part, the curves increase up to a maximum
before falling down to some small value which seems to be
independent of
decreases, indicating that far from the cut-off, the
shape converges to expression (15) of
Fv0(z). On the right part, the curves increase up to a maximum
before falling down to some small value which seems to be
independent of  . When
. When  is multiplied by a constant
factor (here 10-2), the maximum as well as the right part of the
curves are translated by a constant amount. This indicates that for
is multiplied by a constant
factor (here 10-2), the maximum as well as the right part of the
curves are translated by a constant amount. This indicates that for
 small enough, the shape s
small enough, the shape s (z) in the tail (that is
for z large) takes the scaling form
(z) in the tail (that is
for z large) takes the scaling form
We will see that our analysis of section iv does predict
this scaling form. As one expects this shape to coincide with the
asymptotic form (15) of Fv0(z) for 1  z
z  |log
|log  |, the scaling function G(y) should be linear for
small y.
|, the scaling function G(y) should be linear for
small y.
4 Calculation of the velocity for a small cut-off
The first remark we make is that as soon as we introduce a cut-off
through a function a(h) which is everywhere smaller than 1, the
velocity v of the front is lowered compared to the velocity
obtained in the absence of a cut-off. This is easy to check by comparing
a solution h
of the front is lowered compared to the velocity
obtained in the absence of a cut-off. This is easy to check by comparing
a solution h (x,t) of (5) where a(h) is
present and a solution h0(x,t) of (1). If initially
h
(x,t) of (5) where a(h) is
present and a solution h0(x,t) of (1). If initially
h (x,0) < h0(x,0), the solution h
(x,0) < h0(x,0), the solution h will never be
able to take over the solution h0. Indeed, would the two functions
h
will never be
able to take over the solution h0. Indeed, would the two functions
h (x,0) and h0(x,0) coincide for the first time at some
point x, we would have at that point
(x,0) and h0(x,0) coincide for the first time at some
point x, we would have at that point 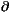 2 h
2 h /
/ 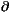 x2
x2 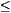
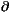 2 h0 /
2 h0 / 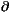 x2 and together with the effect of
a(h) this would bring back the system in the situation where
h
x2 and together with the effect of
a(h) this would bring back the system in the situation where
h (x,t) < h0(x,t) [3, 7]. This shows that v
(x,t) < h0(x,t) [3, 7]. This shows that v
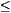 v0.
v0.
For the calculation of the velocity v , we will consider
first the modified Fisher-Kolmogorov equation (5)
when the cut-off function a(h) is simply given by
, we will consider
first the modified Fisher-Kolmogorov equation (5)
when the cut-off function a(h) is simply given by
In this section we will calculate the leading correction to the velocity
when  is small and we will obtain the scaling function G
which appears in (20). Then we will discuss briefly how
our analysis could be extended to more general forms of the cut-off
function a(h) or to other traveling wave equations such as
(9).
is small and we will obtain the scaling function G
which appears in (20). Then we will discuss briefly how
our analysis could be extended to more general forms of the cut-off
function a(h) or to other traveling wave equations such as
(9).
As v is the velocity of the front, its shape
s
is the velocity of the front, its shape
s (z)=h(z+v
(z)=h(z+v t,t) in the asymptotic regime satisfies
t,t) in the asymptotic regime satisfies
When  is small, with the choice (21) for a(h), we
can decompose the range of values of z into three regions:
is small, with the choice (21) for a(h), we
can decompose the range of values of z into three regions:
-
Region I
- where s
 (z) is not small compared to 1.
(z) is not small compared to 1.
- Region II
- where
 < s
< s (z)
(z) 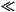 1.
1.
- Region III
- where s
 (z) <
(z) < .
.
In region I, the shape of the front s looks like Fv0
whereas in regions II and III, as s
looks like Fv0
whereas in regions II and III, as s is small, it satisfies
the linear equations
is small, it satisfies
the linear equations
These linear equations (22,23) can be
solved easily. The only problem is to make sure that the solution in
region II and its derivative coincides with Fv0 at the boundary
between I and II and with the solution valid in region III at the
boundary between II and III. If we call 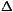 the shift in the
velocity
the shift in the
velocity
and if we note  r ± i
r ± i  i the two roots of the equation
v(
i the two roots of the equation
v( ) = v
) = v , the shape s
, the shape s is given in the three
regions by
is given in the three
regions by
and we can determine the unknown quantities C, D, z0 and v by using the boundary conditions.
by using the boundary conditions.
For large z we know from (15) that Fv0(z) 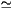 A z
e-
A z
e- 0 z for some A. Therefore, as
0 z for some A. Therefore, as  0-
0-  r ~
r ~
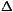 and
and  i ~
i ~ 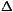 1/2, the boundary conditions between
regions I and II impose, to leading order in
1/2, the boundary conditions between
regions I and II impose, to leading order in 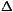 1/2, that C= A/
1/2, that C= A/
 i and D=0.
i and D=0.
At the boundary between regions II and III, we have
s (z)=
(z)= and z=z0. If we impose the continuity of
s
and z=z0. If we impose the continuity of
s and of its first derivative at this point, we get
and of its first derivative at this point, we get
and
Taking the ratio between these two relations leads to
When 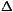 is small,
is small,  r
r 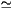
 0 = 1, v
0 = 1, v
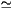 v0 = 2 and
v0 = 2 and  i ~
i ~ 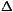 1/2. Thus
the only way to satisfy (27) is to set
1/2. Thus
the only way to satisfy (27) is to set  i z0
i z0 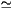
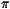 and
and 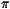 -
-  i z0
i z0 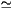
 i ~
i ~
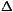 1/2. Therefore, (26) implies to leading order
that z0
1/2. Therefore, (26) implies to leading order
that z0 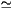 -(log
-(log  )/
)/  0 and the condition
0 and the condition  i
z0
i
z0 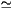
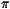 gives
gives
Then, as  i is small, the difference
i is small, the difference 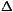 =v0-v
=v0-v is
given by
is
given by
which is the result announced in (7) and (8).
A different cut-off function a(h) should not affect the shape of
s in the region II or the size z0 of region II. Only the
precise matching between regions II and III might be modified and we do
not think that this would change the leading dependency of z0 in
in the region II or the size z0 of region II. Only the
precise matching between regions II and III might be modified and we do
not think that this would change the leading dependency of z0 in
 which controls everything. In fact there are other choices of
the cut-off function a(h) (piecewise constant) for which we could find
the explicit solution in region III, confirming that the precise
form of a(h) does not change (28). The generalization of the
above argument to equations other than (1) (and in particular
to the case studied in sections ii and iii) is
straightforward. Only the form of the linear equation is changed and the
only effect on the final result (7) is that one has to use a
different function v(
which controls everything. In fact there are other choices of
the cut-off function a(h) (piecewise constant) for which we could find
the explicit solution in region III, confirming that the precise
form of a(h) does not change (28). The generalization of the
above argument to equations other than (1) (and in particular
to the case studied in sections ii and iii) is
straightforward. Only the form of the linear equation is changed and the
only effect on the final result (7) is that one has to use a
different function v( ).
).
When expression (7) is compared in figure 1
to the results of the simulations, the agreement is excellent.
Moreover, in region II, one sees from (25)
and (28) that
which also agrees with the scaling form (20).
Recently, for a simple model of evolution [19, 20] governed by a linear equation, the velocity was found to
be the logarithm of the cut-off to the power 1/3. This result was
obtained by an analysis which has some similarities to the one presented
in this section.
5 A stochastic model
Many models described by traveling wave equations originate from a
large scale limit of microscopic stochastic models involving a finite
number N of particles [13, 14, 15, 16]. Here we study such a microscopic model, the
limit of which reduces to (13) when N
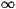 . Our
numerical results, presented below, indicate a large N correction to
the velocity of the form vN
. Our
numerical results, presented below, indicate a large N correction to
the velocity of the form vN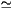 v0 - a (log N)-2
with a coefficient a consistent with the one calculated in
section iv for
v0 - a (log N)-2
with a coefficient a consistent with the one calculated in
section iv for  =1/N.
=1/N.
The model we consider in this section appears in the study of directed
polymers [14] and is, up to minor changes,
equivalent to a model describing the dynamics of hard
spheres [15]. It is a stochastic process
discrete both in time and space with two parameters: N, the number of
particles, and p, a real number between 0 and 1. At time t (t is
an integer), we have N particles on a line at integer positions
x1(t), x2(t), ..., xN(t). Several particles may occupy the
same site. At each time-step, the N positions evolve in the following
way: for each i, we choose two particles ji and j'i at random
among the N particles. (These two particles do not need to be
different.) Then we update xi(t) by
where 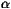 i and
i and 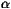 'i are two independent random numbers taking
the value 1 with probability p or 0 with probability 1-p. The
numbers
'i are two independent random numbers taking
the value 1 with probability p or 0 with probability 1-p. The
numbers 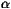 i,
i, 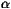 'i, ji and j'i change at each
time-step. Initially (t=0), all particles are at the origin so that we
have xi(0)=0 for all i.
'i, ji and j'i change at each
time-step. Initially (t=0), all particles are at the origin so that we
have xi(0)=0 for all i.
At time t, the distribution of the xi(t) on the line can be
represented by a function h(x,t) which counts the fraction of
particles strictly at the right of x.
Obviously h(x,t) is always an integral multiple of 1/N. At t=0,
we have h(x,0)=1 if x<0 and h(x,0)=0 if x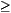 0. One can notice
that the definition of the position Xt of the front used
in (11) coincides with the average position of the N
particles
0. One can notice
that the definition of the position Xt of the front used
in (11) coincides with the average position of the N
particles
Given the positions xi(t) of all the particles (or, equivalently¸
given the function h(x,t)), the xi(t+1) become independent random
variables. Therefore, given h(x,t), the probability for each
particle to have at time t+1 a position strictly larger than x is
given by
The difficulty of the problem comes from the fact that one can only
average h(x,t+1) over a single time-step. On the right hand side
of (34) we see terms like h2(x,t) or h(x-1,t)h(x,t) and
one has to calculate all the correlations of the h(x,t) in order to
find 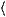 h(x,t+1)
h(x,t+1)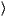 . This makes the problem very
difficult for finite N. However, given h(x,t), the xi(t+1) are
independent and in the limit N
. This makes the problem very
difficult for finite N. However, given h(x,t), the xi(t+1) are
independent and in the limit N
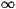 , the fluctuations of h(x,t+1)
are negligible. Therefore, when N
, the fluctuations of h(x,t+1)
are negligible. Therefore, when N
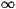 , h(x,t) evolves according
to the deterministic equation (13). As the initial condition
is a step function, we expect the front to move, in the
limit N
, h(x,t) evolves according
to the deterministic equation (13). As the initial condition
is a step function, we expect the front to move, in the
limit N
 , with the minimal velocity v0 of (14).
, with the minimal velocity v0 of (14).
For large but finite N, we expect the correction to the velocity to
have two main origins. First, h(x,t) takes only values which are
integral multiples of 1/N, so that 1/N plays a role similar
to the cut-off  of section ii. Second, h(x,t)
fluctuates around its average and this has the effect of adding noise to
the evolution equation (13). In the rest of this section we
present the results of simulations done for large but finite N and we
will see that the shift in the velocity seems to be very close to the
expression of section iv when
of section ii. Second, h(x,t)
fluctuates around its average and this has the effect of adding noise to
the evolution equation (13). In the rest of this section we
present the results of simulations done for large but finite N and we
will see that the shift in the velocity seems to be very close to the
expression of section iv when  =1/N.
=1/N.
With the most direct way of simulating the model for N finite, it is
difficult to study systems of size much larger than 106. Here we use a
more sophisticated method allowing N to become huge. Our method, which
handles many particles at the same time, consists in iterating directly
h(x,t).
Knowing the function h(x,t) at time t, we want to
calculate h(x,t+1). We call respectively xmin and xmax the
positions of the leftmost and rightmost particles at time t
and l=xmax-xmin+1. In terms of the function h(x,t), one has
0<h(x,t)<1 if and only if xmin x < xmax.
Obviously, all the positions xi(t+1) will lie
between xmin and xmax+1. The probability pk that a given
particle i will be located at position xmin+k at time t+1 is
x < xmax.
Obviously, all the positions xi(t+1) will lie
between xmin and xmax+1. The probability pk that a given
particle i will be located at position xmin+k at time t+1 is
with  h(x,t+1)
h(x,t+1) given
by (34). Obviously, pk
given
by (34). Obviously, pk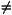 0 only for 0
0 only for 0 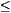 k
k 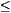 l.
l.
The probability to have, for every k, nk particles at location
xmin+k at time t+1 is given by
Using a random number generator for a binomial distribution,
expression (36) allows to generate random nk. This is
done by calculating n0 according to the distribution
then n1 with
and so on. This method can be iterated to produce the l+1 numbers
n0, n1, ..., nl distributed according to (36).
Then we construct h(x,t+1) by
As the width l of the front is roughly of order log N, this method allows
N to be very large.
Using this method with the generator of random binomial numbers
given in [21], we have measured the velocity vN
of the front for
several choices of p (0.05, 0.25 and 0.45) and for N ranging from 100
to 1016. We measured the velocities with the expression
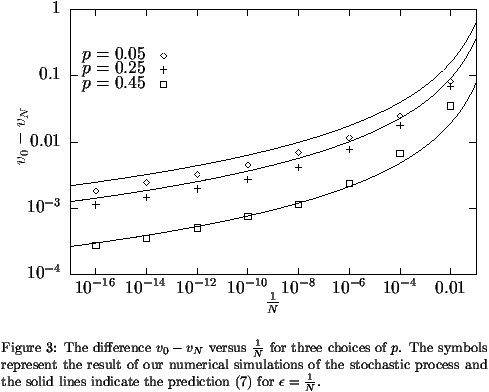
Figure 3 is a log-log plot of the difference v0-vN
versus 1/N compared to the prediction (7)
for  =1/N. The variation of vN when using longer times
or different random numbers were not larger than the size of the symbols.
=1/N. The variation of vN when using longer times
or different random numbers were not larger than the size of the symbols.
We see on figure 3 that the speed vN of the front seems to be
given for large N by
where the coefficient K is not too different from the
prediction (7).
The agreement is however not perfect. The shift v0-vN seems to be
proportional to (log N)-2, but the constant looks on
figure 3 slightly different from the one predicted
by (7). A possible reason for this difference could have
been the discretization of the front: instead of only cutting off the
tail as in sections iii and iv, here the whole
front h(x,t) is constrained to take values multiple of 1/N. One
might think that this could explain this discrepancy. However, we have
checked numerically (the results are not presented in this paper) that
equation (13) with h(x,t) constrained to be a multiple of a
cut-off  does not give results significantly different from the
simpler model of sections iii and iv
with only a single cut-off. So we think that the full
discretization of the front can not be responsible for a different
constant K. The discrepancy observed in figure 3 is more
likely due to the effect of the randomness of the process. It is however
not clear whether this mismatch would decrease for even larger N. It
would be interesting to push further the numerical simulations and check
the N-dependence of the front velocity for very large N.
does not give results significantly different from the
simpler model of sections iii and iv
with only a single cut-off. So we think that the full
discretization of the front can not be responsible for a different
constant K. The discrepancy observed in figure 3 is more
likely due to the effect of the randomness of the process. It is however
not clear whether this mismatch would decrease for even larger N. It
would be interesting to push further the numerical simulations and check
the N-dependence of the front velocity for very large N.
6 Conclusion
We have shown in the present work that a small cut-off  in
the tail of solutions of traveling wave equations has the effect of
selecting a single velocity v
in
the tail of solutions of traveling wave equations has the effect of
selecting a single velocity v for the front. This
velocity v
for the front. This
velocity v converges to the minimal velocity v0 when
converges to the minimal velocity v0 when

 0 and the shift v0-v
0 and the shift v0-v is surprisingly
large (7, 8).
is surprisingly
large (7, 8).
Very slow convergences to the minimal velocity have been observed in a
number of cases [8, 13, 14, 15] as well as the example of
section v. As the effect of the cut-off on the velocity is
large, it is reasonable to think that it would not be much affected by
the presence of noise. The example of section v shows that
the cut-off alone gives at least the right order of magnitude for the
shift and it would certainly be interesting to push further the
simulations for this particular model to see whether the analysis
of section iv should be modified by the noise. The numerical
method used in section v to study a very large (N~
1016) system was very helpful to observe a logarithmic behavior. We
did not succeed to check in earlier
works [13, 14, 15, 22] whether the correction
was logarithmic, mostly because the published data were usually too noisy
or obtained on a too small range of the parameters. Still even if the
cut-off was giving the main contribution to the shift of the velocity,
other properties would remain very specific to the presence of noise
like the diffusion of the position of the
front [16].
Our approach of section iv shows that the effect of a small
cut-off is the existence of a scaling
form (20, 30) which describes the change
in the shape of the front in its steady state. The effect of initial
conditions for usual traveling wave equations (with no cut-off) leads to
a very similar scaling form for the change in the shape of the front in
the transient regime. This is explained in the appendix where
we show how the logarithmic shift of the position of a front due to
initial conditions [10, 23]
can be recovered.
A Effect of initial conditions on the position and on the shape of
the front
In this appendix we show that ideas very similar to those developed in
section iv allow one to calculate the position and the shape at
time t of a front evolving according to (1), or to a similar
equation, given its initial shape. The main idea is that in the long time
limit, there is a region of size (t)1/2 ahead of the front which
keeps the memory of the initial condition. We will recover in particular
the logarithmic shift in the position of the front due to the initial
condition [10, 23], namely
that if the initial shape is a step function
then the position Xt of the front at time t increases like
More generally, if initially
we will show that for 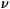 >-2
>-2
whereas the shift is given by (A2) for 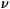 <-2.
Here, there is no cut-off but the transient behavior in the long time
limit gives rise to a scaling function very similar to the one discussed
in section iv.
<-2.
Here, there is no cut-off but the transient behavior in the long time
limit gives rise to a scaling function very similar to the one discussed
in section iv.
If we write the position of the front at time t as
we observed numerically (as in figure 2 of
section iii) and we are going to see
in the following that the shape of the front takes for large t the
scaling form
very similar to (20, 30).
If we use (A5) and (A6) into the linearized
form of equation (1), we get using, the fact that v0=2 and
 0=1,
0=1,
where z=(x-Xt)t-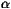 .
By writing that the leading orders of the different terms
of (A7) are comparable, we see that we must have
.
By writing that the leading orders of the different terms
of (A7) are comparable, we see that we must have
for some  , and that the right hand side of (A7) is
negligible. Therefore, the equation satisfied by G is
, and that the right hand side of (A7) is
negligible. Therefore, the equation satisfied by G is
and the position of the front is given by
As in section iv, we expect that as t
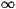 , the front
will approach its limiting form and therefore that for z small, the
shape will look like (15). Therefore we choose the
solution G
, the front
will approach its limiting form and therefore that for z small, the
shape will look like (15). Therefore we choose the
solution G (z) of (A10) which is linear at z=0.
This solution can be written as an infinite sum
(z) of (A10) which is linear at z=0.
This solution can be written as an infinite sum
(The second expression is not valid when  is a non-positive
integer.)
is a non-positive
integer.)
To determine  , one can notice that the scaling
form (A6) has to match the initial condition when x is
large and t of order 1. We thus need to calculate the asymptotic
behavior of G(z) when z is large.
, one can notice that the scaling
form (A6) has to match the initial condition when x is
large and t of order 1. We thus need to calculate the asymptotic
behavior of G(z) when z is large.
For certain values of  , there exist closed expressions of the
sum (A12). For instance,
, there exist closed expressions of the
sum (A12). For instance,
One can check directly on (A10) that G has a
symmetry
has a
symmetry
For any  , one can obtain the large z
behavior of G(z). To do so, we note that for
, one can obtain the large z
behavior of G(z). To do so, we note that for  >0, one can
rewrite (A12) as
>0, one can
rewrite (A12) as
For 0< <1, the second integral in (A15) has a non
zero limit and this gives the asymptotic behavior of G
<1, the second integral in (A15) has a non
zero limit and this gives the asymptotic behavior of G (z)
(z)
From (A12), one can also show that
implying that (A16) remains valid for
all  except for
except for  =3/2, 5/2, 7/2, etc.,
where the amplitude in (A16) vanishes.
For these values of
=3/2, 5/2, 7/2, etc.,
where the amplitude in (A16) vanishes.
For these values of  , G
, G (z)
decreases faster than a power law (see (A13)).
(z)
decreases faster than a power law (see (A13)).
The functions G calculated so far are acceptable scaling
functions for the shape of the front only for
calculated so far are acceptable scaling
functions for the shape of the front only for 
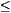 3/2. Indeed,
one can see in (A16) that for 3/2<
3/2. Indeed,
one can see in (A16) that for 3/2< <5/2
the function G
<5/2
the function G (z) is negative for large z. In fact, for all
(z) is negative for large z. In fact, for all
 >3/2, this function changes its sign at least once, so that
the scaling form (A6) is not reachable for an initial
h(x,0) which is always positive. It is only for
>3/2, this function changes its sign at least once, so that
the scaling form (A6) is not reachable for an initial
h(x,0) which is always positive. It is only for 
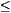 3/2 that
G
3/2 that
G remains positive for all z>0.
remains positive for all z>0.
Looking at the asymptotic form (A16), we see that if
initially h(x,0)=x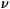 e-
e- 0 x, the only function G
0 x, the only function G (z)
which has the right large z behavior is such that 1-2
(z)
which has the right large z behavior is such that 1-2 =
=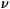 , and
this gives, together with (A11), the
expression (A4) for the shift of the position. As the
cases
, and
this gives, together with (A11), the
expression (A4) for the shift of the position. As the
cases  >3/2 are not reachable, all initial conditions
corresponding to
>3/2 are not reachable, all initial conditions
corresponding to 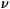 <-2 or steeper (such as step functions) give rise
to G3/2 and the shift in position given by (A2).
<-2 or steeper (such as step functions) give rise
to G3/2 and the shift in position given by (A2).
All the analysis of this appendix can be extended to other
traveling wave equations such as (13), with more general
functions v( ) (having a non-degenerate minimum at
) (having a non-degenerate minimum at  0) as
in (14). Then the
expressions (A2, A4) of the shift
become
0) as
in (14). Then the
expressions (A2, A4) of the shift
become
and
We thank C. Appert, V. Hakim and J.L. Lebowitz for useful discussions.
References
- [1]
-
R. A. Fisher, ``The Wave of Advance of Advantageous Genes,'' Annals of Eugenics
7, 355--369 (1937).
- [2]
-
A. Kolmogorov, I. Petrovsky, and N. Piscounov, ``Étude de l'Équation de la
Diffusion avec Croissance de la Quantité de Matière et son Application
à un Problème Biologique,'' Moscou Univ. Bull. Math. A 1, 1 (1937).
- [3]
-
D. G. Aronson and H. F. Weinberger, ``Multidimensional Nonlinear Diffusion
Arising in Population Genetics,'' Advances in Mathematics 30, 33--76
(1978).
- [4]
-
G. Dee and J. S. Langer, ``Propagating Pattern Selection,'' Physical Review
Letters 50, 383--386 (1983).
- [5]
-
M. Bramson, P. Calderoni, A. D. Masi, P. Ferrari, J. L. Lebowitz, and R. H.
Schonmann, ``Microscopic Selection Principle for a Diffusion-Reaction
Equation,'' Journal of Statistical Physics 45, 905--920 (1986).
- [6]
-
W. van Saarloos, ``Front Propagation into Unstable States. Linear Versus
Nonlinear Marginal Stability and Rate of Convergence,'' Physical Review A
39, 6367--6390 (1989).
- [7]
-
P. Collet and J.-P. Eckmann, Instabilities and Fronts in Extended Systems
(Princeton University Press, 1990).
- [8]
-
A. R. Kerstein, ``Computational Study of Propagating Fronts in a Lattice-Gas
Model,'' Journal of Statistical Physics 45, 921--931 (1986).
- [9]
-
D. G. Aronson and H. F. Weinberger, ``Nonlinear Diffusion in Population
Genetics, Combustion, and Nerve Propagation,'' Lecture Notes in Mathematics
446, 5--49 (1975).
- [10]
-
M. Bramson, Convergence of Solutions of the Kolmogorov Equation to
Traveling Waves, No. 285 in Memoirs of the American Mathematical
Society (AMS, 1983).
- [11]
-
W. van Saarloos, ``Dynamical Velocity Selection: Marginal Stability,'' Physical
Review Letters 58, 2571--2574 (1987).
- [12]
-
W. van Saarloos, ``Front Propagation into Unstable States: Marginal Stability
as a Dynamical Mechanism for Velocity Selection,'' Physical Review A 37, 211--229 (1988).
- [13]
-
H. P. Breuer, W. Huber, and F. Petruccione, ``Fluctuation Effects on Wave
Propagation in a Reaction-Diffusion Process,'' Physica D 73, 259--273
(1994).
- [14]
-
J. Cook and B. Derrida, ``Lyapunov Exponents of Large, Sparse Random Matrices
and the Problem of Directed Polymers with Complex Random Weights,'' Journal
of Statistical Physics 61, 961--986 (1990).
- [15]
-
R. van Zon, H. van Beijeren, and C. Dellago, ``Largest Lyapunov Exponent for
Many Particle Systems at Low Densities,'' (preprint 1997).
- [16]
-
H. P. Breuer, W. Huber, and F. Petruccione, ``The Macroscopic Limit in a
Stochastic Reaction-Diffusion Process,'' Europhysics Letters 30, 69--74
(1995).
- [17]
-
B. Derrida and H. Spohn, ``Polymers on Disordered Trees, Spin Glasses, and
Traveling Waves,'' Journal of Statistical Physics 51, 817--840 (1988).
- [18]
-
B. Derrida, ``Mean field theory of directed polymers in a random medium,''
Physica Scripta 38, 6--12 (1991).
- [19]
-
D. A. Kessler, H. Levine, D. Ridgway, and L. Tsimring, ``Evolution on a Smooth
Landscape,'' (preprint 1996).
- [20]
-
L. Tsimring, H. Levine, and D. A. Kessler, ``RNA Virus Evolution via a
Fitness-Space Model,'' Physical Review Letters 76, 4440--4443 (1996).
- [21]
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes in C (Cambridge University Press, 1994).
- [22]
-
A. R. Kerstein, ``A Two-Particle Representation of Front Propagation in
Diffusion-Reaction Systems,'' Journal of Statistical Physics 53,
703--712 (1988).
- [23]
-
M. D. Bramson, ``Maximal Displacement of Branching Brownian motion,''
Communications In Pure and Applied Mathematics 31, 531--581 (1978).
This document was translated from LATEX by HEVEA.
 on the velocity
of a traveling wave in one dimension. Simulations done over more than ten
orders of magnitude as well as a simple theoretical argument indicate
that the effect of the cut-off
on the velocity
of a traveling wave in one dimension. Simulations done over more than ten
orders of magnitude as well as a simple theoretical argument indicate
that the effect of the cut-off  is to select a single velocity
which converges when
is to select a single velocity
which converges when 
 0 to the one predicted by the marginal
stability argument. For small
0 to the one predicted by the marginal
stability argument. For small  , the shift in velocity has the
form K(log
, the shift in velocity has the
form K(log )-2 and our prediction for the constant K
agrees very well with the results of our simulations. A very similar
logarithmic shift appears in more complicated situations, in particular in
finite size effects of some microscopic stochastic systems. Our
theoretical approach can also be extended to give a simple way of
deriving the shift in position due to initial conditions in the
Fisher-Kolmogorov or similar equations.
)-2 and our prediction for the constant K
agrees very well with the results of our simulations. A very similar
logarithmic shift appears in more complicated situations, in particular in
finite size effects of some microscopic stochastic systems. Our
theoretical approach can also be extended to give a simple way of
deriving the shift in position due to initial conditions in the
Fisher-Kolmogorov or similar equations.

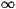 and h(x,0)
and h(x,0) 
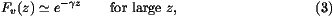

 is arbitrary, this shows the well known fact that the
range of possible velocities is v
is arbitrary, this shows the well known fact that the
range of possible velocities is v 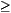 2. The minimal velocity v0=2
is reached for
2. The minimal velocity v0=2
is reached for 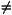 0 is to introduce a cut-off in the tail of the front, and
that this changes noticeably the speed.
0 is to introduce a cut-off in the tail of the front, and
that this changes noticeably the speed.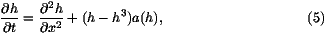
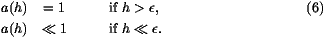
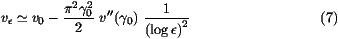

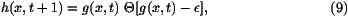
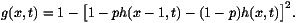
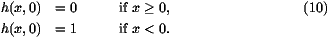
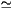 1 behind the front and h(x,t)
1 behind the front and h(x,t)
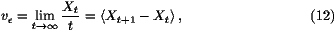
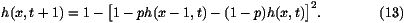
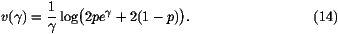
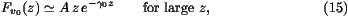
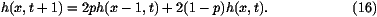



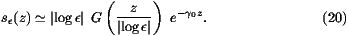
 z
z 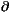 2 h
2 h
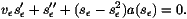
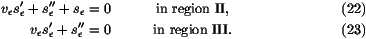
 the shift in the
velocity
the shift in the
velocity

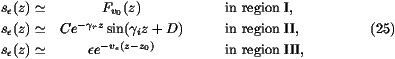

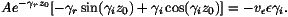

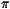 and
and 
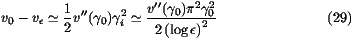
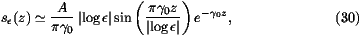
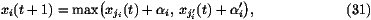
 i and
i and 
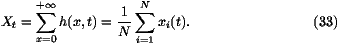
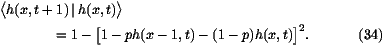
 h(x,t+1)
h(x,t+1) . This makes the problem very
difficult for finite N. However, given h(x,t), the xi(t+1) are
independent and in the limit N
. This makes the problem very
difficult for finite N. However, given h(x,t), the xi(t+1) are
independent and in the limit N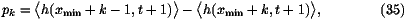
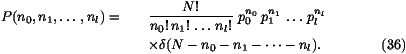
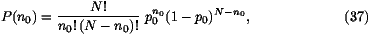
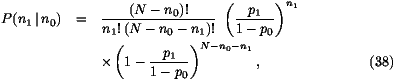
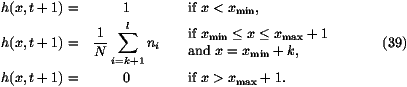


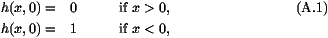

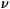 >-2
>-2


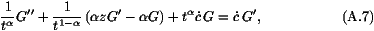

 , and that the right hand side of (A7) is
negligible. Therefore, the equation satisfied by G is
, and that the right hand side of (A7) is
negligible. Therefore, the equation satisfied by G is