Ising dual 4x4.py
From Werner KRAUTH
| Revision as of 21:28, 19 October 2015 Werner (Talk | contribs) ← Previous diff |
Current revision Werner (Talk | contribs) (→Program) |
||
| Line 1: | Line 1: | ||
| - | This page presents the program Ising_dual_4x4.py, that checks the Kramers-Wannier duality for a finite 4x4 Ising model with periodic boundary conditions. | + | This page presents the program Ising_dual_4x4.py, that checks Kramers-Wannier duality for a finite 4x4 Ising model with periodic boundary conditions. |
| __FORCETOC__ | __FORCETOC__ | ||
| =Reference= | =Reference= | ||
| - | This program is discussed in [[ICFP_Stat_Physics_2015|Lecture 4]] of my ICFP course 2015 on Statistical physics. The Lectures is called "Exact computations in the two-dimensional Ising model (Kac-Ward)". | + | This program is discussed in [[ICFP_Stat_Physics_2019|Lecture 07]] of my 2019 ICFP lecture on Statistical physics: "Two-dimensional Ising model: From Kramers & Wannier to Kac & Ward". |
| + | |||
| =Description= | =Description= | ||
| - | The program inputs the density of states of the 4x4 lattice with periodic boundary conditions (that can be computed by [[enumerate_ising_dos.py|the enumerate-Ising program]]. For any beta it computes a beta_tilde, and then compares Z and Z_tilde. At low temperature, where only short loops come up, everything is OK, but at higher temperature, the winding paths create a problem. This is discussed in the lecture notes. | + | We consider the 4x4 Ising model with periodic boundary conditions. A duality relation was discovered by Kramers and Wannier. It means that, morally, any loop in the high-temperature expansion also appears in the low-temperature expansion of the partition function: |
| + | [[Image:Square Lattice duality without pbc.jpg]] | ||
| - | =Program= | + | However, this duality is not exact for finite lattices, as there are loops (spanning the entire lattice) that, due to the periodic boundary conditions, cannot separate different domains: |
| + | [[Image:Ising dual finite difference.jpg]] | ||
| - | import math | + | It follows that the duality relation between the partition functions at two temperatures related by the duality relation is not exact. This is what we check with the below program. |
| + | |||
| + | Using the density of states (the dictionary "dos" is from SMAC Table 5.2), we can compute the partition functions Z and Z_tilde at inverse temperatures beta and beta_tilde that are related by the Kramers-Wannier duality relation. | ||
| + | |||
| + | At low temperatures, the corresponding partition functions are related to each other by the factor that stems from duality. | ||
| + | At higher temperatures, this is no longer true as there are terms in the high-temperature expansion that do not appear in the low-temperature expansion. Note that taking the transformation from beta -> beta_tilde a second time brings us back to beta in other words: beta_tilde_tilde = beta | ||
| + | |||
| + | NB: The difference we discuss here (for the 4x4 lattice) go away for larger lattices, as the differences between the loops in the high-temperature expansion and those in the low-temperature expansion show up at order L only. | ||
| + | |||
| + | =Program= | ||
| + | |||
| + | NB: dos stands for the density of states, the number of configurations of energy E (-32, -24, ...), in the 4x4 two-dimensional Ising model without periodic boundary conditions. The dos is obtained from my book, where it is obtained through exact enumeration. | ||
| + | |||
| N = 16 | N = 16 | ||
| - | dos = { -32: 2, -24: 32, -20: 64, -16: 424, -12: 1728, -8: 6688, | + | dos = { -32: 2, -24: 32, -20: 64, -16: 424, -12: 1728, -8: 6688, |
| - | -4: 13568, 0: 20524, 4: 13568, 8: 6688, 12: 1728, 16: 424, 20: 64, 24: 32, 32: 2} | + | -4: 13568, 0: 20524, 4: 13568, 8: 6688, 12: 1728, |
| - | list_T = [0.1 + 0.1 * i for i in range(80)] | + | 16: 424, 20: 64, 24: 32, 32: 2} |
| + | list_T = [0.1 + 0.2 * i for i in range(20)] | ||
| + | print 'T, Z factor / Z_tilde' | ||
| for T in list_T: | for T in list_T: | ||
| beta = 1.0 / T | beta = 1.0 / T | ||
| - | beta_tilde = math.atanh(math.exp(-2 * beta)) | + | beta_tilde = math.atanh(math.exp(-2.0 * beta)) |
| - | Z = 0.0 | + | T_tilde = 1.0 / beta_tilde |
| - | Z_tilde = 0.0 | + | |
| factor = 2 ** (N - 1) * (math.cosh(beta_tilde)) ** (2 * N) * \ | factor = 2 ** (N - 1) * (math.cosh(beta_tilde)) ** (2 * N) * \ | ||
| (math.tanh(beta_tilde)) ** N | (math.tanh(beta_tilde)) ** N | ||
| - | for E in dos.keys(): | + | Z = sum(math.exp(- beta * E) * dos[E] for E in dos.keys()) |
| - | weight = math.exp(- beta * E) * dos[E] | + | Z_tilde = sum(math.exp(- beta_tilde * E) * dos[E] for E in dos.keys()) |
| - | weight_tilde = math.exp(- beta_tilde * E) * dos[E] | + | print T, (Z * factor) / Z_tilde |
| - | Z += weight | + | |
| - | Z_tilde += weight_tilde | + | |
| - | print T, (Z * factor) / Z_tilde, ' Temperature, Z * factor / Z_tilde' | + | |
| - | + | ||
| =Version= | =Version= | ||
Current revision
This page presents the program Ising_dual_4x4.py, that checks Kramers-Wannier duality for a finite 4x4 Ising model with periodic boundary conditions.
Contents |
Reference
This program is discussed in Lecture 07 of my 2019 ICFP lecture on Statistical physics: "Two-dimensional Ising model: From Kramers & Wannier to Kac & Ward".
Description
We consider the 4x4 Ising model with periodic boundary conditions. A duality relation was discovered by Kramers and Wannier. It means that, morally, any loop in the high-temperature expansion also appears in the low-temperature expansion of the partition function:
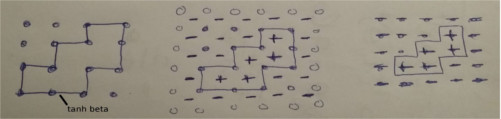
However, this duality is not exact for finite lattices, as there are loops (spanning the entire lattice) that, due to the periodic boundary conditions, cannot separate different domains:
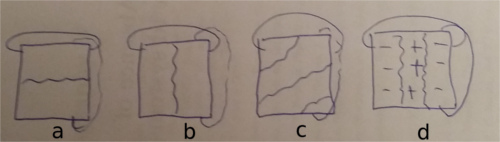
It follows that the duality relation between the partition functions at two temperatures related by the duality relation is not exact. This is what we check with the below program.
Using the density of states (the dictionary "dos" is from SMAC Table 5.2), we can compute the partition functions Z and Z_tilde at inverse temperatures beta and beta_tilde that are related by the Kramers-Wannier duality relation.
At low temperatures, the corresponding partition functions are related to each other by the factor that stems from duality.
At higher temperatures, this is no longer true as there are terms in the high-temperature expansion that do not appear in the low-temperature expansion. Note that taking the transformation from beta -> beta_tilde a second time brings us back to beta in other words: beta_tilde_tilde = beta
NB: The difference we discuss here (for the 4x4 lattice) go away for larger lattices, as the differences between the loops in the high-temperature expansion and those in the low-temperature expansion show up at order L only.
Program
NB: dos stands for the density of states, the number of configurations of energy E (-32, -24, ...), in the 4x4 two-dimensional Ising model without periodic boundary conditions. The dos is obtained from my book, where it is obtained through exact enumeration.
N = 16
dos = { -32: 2, -24: 32, -20: 64, -16: 424, -12: 1728, -8: 6688,
-4: 13568, 0: 20524, 4: 13568, 8: 6688, 12: 1728,
16: 424, 20: 64, 24: 32, 32: 2}
list_T = [0.1 + 0.2 * i for i in range(20)]
print 'T, Z factor / Z_tilde'
for T in list_T:
beta = 1.0 / T
beta_tilde = math.atanh(math.exp(-2.0 * beta))
T_tilde = 1.0 / beta_tilde
factor = 2 ** (N - 1) * (math.cosh(beta_tilde)) ** (2 * N) * \
(math.tanh(beta_tilde)) ** N
Z = sum(math.exp(- beta * E) * dos[E] for E in dos.keys())
Z_tilde = sum(math.exp(- beta_tilde * E) * dos[E] for E in dos.keys())
print T, (Z * factor) / Z_tilde
Version
See history for version information.
Categories: Python | ICFP
