SSEPCompact.py

From Werner KRAUTH

Revision as of 12:38, 10 June 2024 Werner (Talk | contribs) ← Previous diff		Revision as of 12:40, 10 June 2024 Werner (Talk | contribs) Next diff →
Line 38:		Line 38:
	Text = 'Total time = ' + str(prefactor) + ' * N ^ ' + str(exponent) + ' * log N'		Text = 'Total time = ' + str(prefactor) + ' * N ^ ' + str(exponent) + ' * log N'
	print(' ' * (NSites// 2 + 1 - len(Text) // 2) + Text + ' ' * (NSites// 2 + 1 - len(Text) // 2))		print(' ' * (NSites// 2 + 1 - len(Text) // 2) + Text + ' ' * (NSites// 2 + 1 - len(Text) // 2))
		+
		+	This example program performs a large number of iterations of the Monte Carlo algorithm for the Symmetric Simple Exclusion Process, and plots 40 lines of output over the entire simulation time.
	==Output==		==Output==

---

Revision as of 12:40, 10 June 2024

Contents 1 Context 2 Python program 3 Output 4 Further Information 5 References

Context

This page is part of my 2024 Beg Rohu Lectures on "The second Markov chain revolution" at the Summer School "Concepts and Methods of Statistical Physics" (3 - 15 June 2024).

Python program

import math
import random
exponent = 3.0
alpha = 0.5
prefactor = 1.0
NPart = 64; NSites = 2 * NPart
NIter = int(prefactor * NPart ** exponent * math.log(NPart))
NStrob = NIter // 40
Conf = [1] * NPart + [0] * (NSites - NPart)
Active = random.randint (0, NSites - 1)
while Conf[Active] != 1:
    Active = random.randint(0, NSites - 1)
Text = 'Periodic SSEP, N= ' + str(NPart) + ', L= ' + str(NSites)
print(' ' * (NSites// 2 + 1 - len(Text) // 2) + Text + ' ' * (NSites// 2 + 1 - len(Text) // 2))
print('-' * (NSites + 2))
for iter in range(NIter):
    Active = random.randint (0, NSites - 1)
    while Conf[Active] != 1: Active = random.randint(0, NSites - 1)
    Step = random.choice([-1,1])
    NewActive = (Active + Step) % NSites
    if Conf[NewActive] == 0: Conf[Active], Conf[NewActive] = 0, 1
    PP = '|'
    ktot= 0
    for k in range(NSites):
        if Conf[k] == 0:
            PP += ' '
        else:
           ktot += 1
           if ktot != NPart / 2: PP += 'X'
           else: PP += '|'
    if iter % NStrob == 0: print(PP)
print('-' * (NSites + 2))
Text = 'Total time = ' + str(prefactor) +  ' *  N ^ ' + str(exponent) + ' * log N'
print(' ' * (NSites// 2 + 1 - len(Text) // 2) + Text + ' ' * (NSites// 2 + 1 - len(Text) // 2))

This example program performs a large number of iterations of the Monte Carlo algorithm for the Symmetric Simple Exclusion Process, and plots 40 lines of output over the entire simulation time.

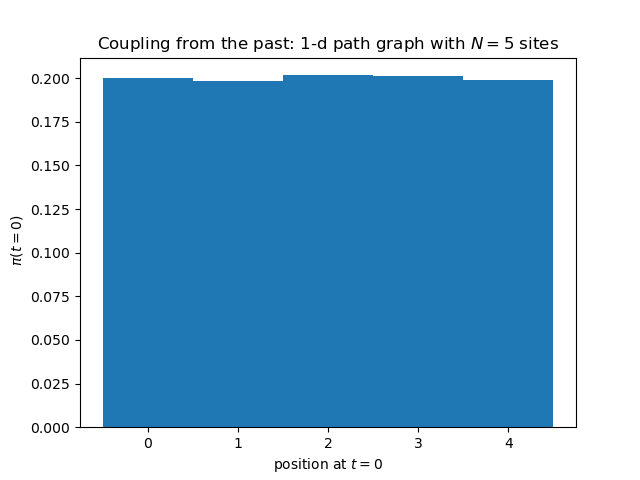
Output

Here is output of the above Python program. The histogram is absolutely flat, without any corrections. But this is normal, given that the simulation has run, for each of the realizations of the random map, an infinite number of iterations.

Further Information

References