From Werner KRAUTH

Revision as of 21:36, 23 September 2015 Werner (Talk | contribs) ← Previous diff		Current revision Werner (Talk | contribs)
Line 1:		Line 1:
	__FORCETOC__		__FORCETOC__
	S. C. Kapfer and W. Krauth		S. C. Kapfer and W. Krauth
-	''Sampling from a polytope and hard-disk Monte Carlo'' J. Phys.: Conf. Ser. 454 012031 (2013)	+	''Sampling from a polytope and hard-disk Monte Carlo'' J. Phys.: Conf. Ser. 454 012031 (2013) Open Access
	=Paper=		=Paper=

---

Current revision

S. C. Kapfer and W. Krauth Sampling from a polytope and hard-disk Monte Carlo J. Phys.: Conf. Ser. 454 012031 (2013) Open Access

Contents 1 Paper

Paper

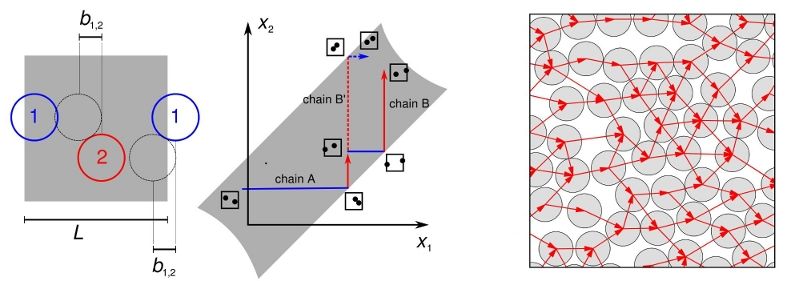
Abstract The hard-disk problem, the statics and the dynamics of equal two-dimensional hard spheres in a periodic box, has had a profound influence on statistical and computational physics. Markov-chain Monte Carlo and molecular dynamics were first discussed for this model. Here we reformulate hard-disk Monte Carlo algorithms in terms of another classic problem, namely the sampling from a polytope. Local Markov-chain Monte Carlo, as proposed by Metropolis et al. in 1953, appears as a sequence of random walks in high-dimensional polytopes, while the moves of the more powerful event-chain algorithm correspond to molecular dynamics evolution. We determine the convergence properties of Monte Carlo methods in a special invariant polytope associated with hard-disk configurations, and the implications for convergence of hard-disk sampling. Finally, we discuss parallelization strategies for event-chain Monte Carlo and present results for a multicore implementation.

Electronic version (from arXiv, original version)

Final version (open access, available to everyone)