Diffusion CFTP.py
From Werner KRAUTH
| Revision as of 08:46, 9 June 2024 Werner (Talk | contribs) (→Python program) ← Previous diff |
Revision as of 11:08, 9 June 2024 Werner (Talk | contribs) Next diff → |
||
| Line 6: | Line 6: | ||
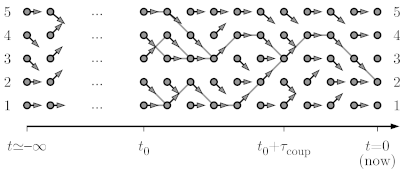
| [[Image:One d cftp.png|left|600px|border|Coupling-from-the-past approach to sampling.]] | [[Image:One d cftp.png|left|600px|border|Coupling-from-the-past approach to sampling.]] | ||
| <br clear="all" /> | <br clear="all" /> | ||
| - | At time t=-infinity, as shown, the pebble starts on configuration 1, so that, by time t=0, it must sample the stationary distribution (the uniform distribution on the five sites). The below program constructs just as many set of arrows as needed to conclude on where it finishes it infinitely long journey. | + | At time t=-infinity, as shown, the pebble starts on configuration 1 so that, by time t=0, it must sample the stationary distribution (the uniform distribution on the five sites). The below program constructs just as many set of arrows as needed to conclude on where it finishes it infinitely long journey. |
| ==Python program== | ==Python program== | ||
| Line 46: | Line 46: | ||
| ==Further Information== | ==Further Information== | ||
| - | #Item1 1 | + | * Rather than to run the simulation until t=0, one might be tempted to stop it as soon as the configurations have coupled at some time t < 0. This is tested in the following program, but it is wrong for obvious reasons: The goal was to infer the position at t=0 of a simulation that has run since time t=-infinity. |
| - | #Item 2 | + | * The above program is easily adapted to a non-uniform stationary distribution pi(1),...,pi(N-1), and its output is then equivalent to what we would obtain using the direct-sampling algorithms that I discussed in BegRohu Lecture 1, first and foremost [[Walker.py| Walker's algorithm]]. However, Walker's algorithm always requires the stationary probabilities on the sample space to be evaluated and rearranged in some way, whereas the CFTP approach to Markov chains can be often applied for huge sample spaces Omega, way larger than what can be listed. |
| - | #Item 3 | + | |
| - | #Item2 4 | + | |
| - | + | ||
| - | Rather than to run the simulation until t=0, one might be tempted to stop it as soon as the configurations have coupled at some time t < 0. This is tested in the following program, but it is wrong for obvious reasons: The goal was to infer the position at t=0 of a simulation that has run since time t=-infinity. | + | |
| ==References== | ==References== | ||
Revision as of 11:08, 9 June 2024
Contents |
Context
This page is part of my 2024 Beg Rohu Lectures on "The second Markov chain revolution" at the Summer School "Concepts and Methods of Statistical Physics" (3 - 15 June 2024).
In the example of a particle diffusing on a path graph with five sites, with moves from configuration i to [i-1, i, i] being proposed, we consider the formulation of a Markov chain in terms of random maps, but run from time t=-infinity up to time t=0.
At time t=-infinity, as shown, the pebble starts on configuration 1 so that, by time t=0, it must sample the stationary distribution (the uniform distribution on the five sites). The below program constructs just as many set of arrows as needed to conclude on where it finishes it infinitely long journey.
Python program
import random
import matplotlib.pyplot as plt
N = 5
pos = []
for stat in range(100000):
all_arrows = {}
time_tot = 0
while True:
time_tot -= 1
arrows = [random.choice([-1, 0, 1]) for i in range(N)]
if arrows[0] == -1: arrows[0] = 0
if arrows[N - 1] == 1: arrows[N - 1] = 0
all_arrows[time_tot] = arrows
positions = set(range(0, N))
for t in range(time_tot, 0):
positions = set([b + all_arrows[t][b] for b in positions])
if len(positions) == 1: break
a = positions.pop()
pos.append(a)
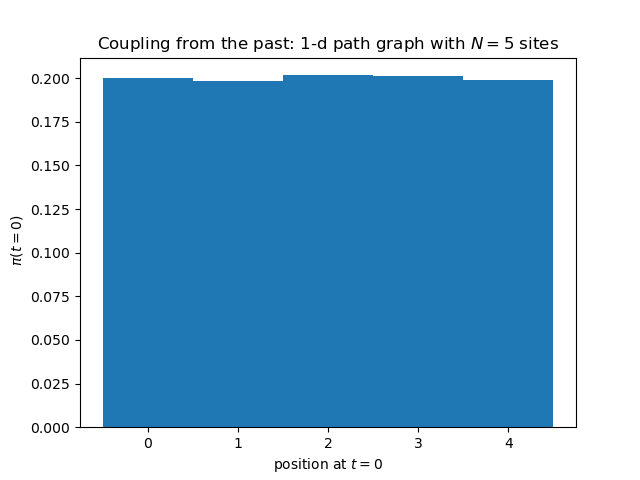
plt.title('Backward coupling: 1-d with walls: position at t=0')
plt.hist(pos, bins=N, range=(-0.5, N - 0.5), density=True)
plt.savefig('backward_position_t0.png')
plt.show()
In this program, note that "arrows" is a list of lists (the arrows for each position 0,1,...,N - 1) It is then added to the dictionary all_arrows. This dictionary contains exactly the random map of arrows in the above picture, from time time_tot to time -1.
Output
Here is output of the above Python program. The histogram is absolutely flat, without any corrections. But this is normal, given that the simulation has run, for each of the realizations of the random map, an infinite number of iterations.
Further Information
- Rather than to run the simulation until t=0, one might be tempted to stop it as soon as the configurations have coupled at some time t < 0. This is tested in the following program, but it is wrong for obvious reasons: The goal was to infer the position at t=0 of a simulation that has run since time t=-infinity.
- The above program is easily adapted to a non-uniform stationary distribution pi(1),...,pi(N-1), and its output is then equivalent to what we would obtain using the direct-sampling algorithms that I discussed in BegRohu Lecture 1, first and foremost Walker's algorithm. However, Walker's algorithm always requires the stationary probabilities on the sample space to be evaluated and rearranged in some way, whereas the CFTP approach to Markov chains can be often applied for huge sample spaces Omega, way larger than what can be listed.
References
This program illustrates the coupling-from-the-past approach to Markov-chain sampling introduced by Propp and Wilson, in 1997.
The reference is: