From Werner KRAUTH

This page presents the program Ising_dual_4x4.py, that checks Kramers-Wannier duality for a finite 4x4 Ising model with periodic boundary conditions.

Contents 1 Reference 2 Description 3 Program 4 Version

Reference

This program is discussed in Lecture 06 of my ICFP lectures 2016 on Statistical physics. The Lecture is called "Two-dimensional Ising model: From Kramers & Wannier to Kac & Ward".

Description

We consider the 4x4 Ising model with periodic boundary conditions. A duality relation was uncovered by Kramers and Wannier. It means that, morally, any loop in the high-temperature expansion also appears in the low-temperature expansion of the partition function:

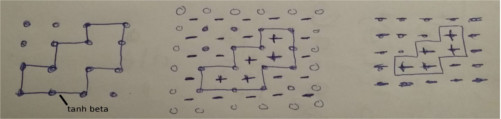
However, this duality is not exact for finite lattices, as there are loops (spanning the entire lattice) that, due to the periodic boundary conditions, cannot separate different domains:

It follows that the duality relation between the partition functions at to temperatures related by the duality relation is not exact. This is what we check with the below program.

Using the density of states (the dictionary "dos" is from SMAC Table 5.2), we can compute the partition functions Z and Z_tilde at inverse temperatures beta and beta_tilde that are related by the Kramers-Wannier duality relation.

At low temperatures, the corresponding partition functions are related to each other by the factor that stems from duality.

At higher temperatures, this is no longer true as there are terms in the high-temperature expansion that do not appear in the low-temperature expansion. Note that taking the transformation from beta -> beta_tilde a second time brings us back to beta in other words: beta_tilde_tilde = beta

Program

N = 16
dos = { -32: 2, -24: 32, -20: 64, -16: 424, -12: 1728, -8: 6688, 
-4: 13568, 0: 20524, 4: 13568, 8: 6688, 12: 1728, 
16: 424, 20: 64, 24: 32, 32: 2}
list_T = [0.1 + 0.2 * i for i in range(20)]
print 'T, Z factor / Z_tilde'
for T in list_T:
    beta = 1.0 / T
    beta_tilde = math.atanh(math.exp(-2.0 * beta))
    T_tilde = 1.0 / beta_tilde
    factor = 2 ** (N - 1) * (math.cosh(beta_tilde)) ** (2 * N) * \
            (math.tanh(beta_tilde)) ** N
    Z = sum(math.exp(- beta * E) * dos[E] for E in dos.keys())
    Z_tilde = sum(math.exp(- beta_tilde * E) * dos[E] for E in dos.keys())
    print T, (Z * factor) / Z_tilde

Version

See history for version information.