SSEPCompact.py
From Werner KRAUTH
Contents |
Context
This page is part of my 2024 Beg Rohu Lectures on "The second Markov chain revolution" at the Summer School "Concepts and Methods of Statistical Physics" (3 - 15 June 2024).
Python program
import math
import random
exponent = 3.0
alpha = 0.5
prefactor = 1.0
NPart = 64; NSites = 2 * NPart
NIter = int(prefactor * NPart ** exponent * math.log(NPart))
NStrob = NIter // 40
Conf = [1] * NPart + [0] * (NSites - NPart)
Active = random.randint (0, NSites - 1)
while Conf[Active] != 1:
Active = random.randint(0, NSites - 1)
Text = 'Periodic SSEP, N= ' + str(NPart) + ', L= ' + str(NSites)
print(' ' * (NSites// 2 + 1 - len(Text) // 2) + Text + ' ' * (NSites// 2 + 1 - len(Text) // 2))
print('-' * (NSites + 2))
for iter in range(NIter):
Active = random.randint (0, NSites - 1)
while Conf[Active] != 1: Active = random.randint(0, NSites - 1)
Step = random.choice([-1,1])
NewActive = (Active + Step) % NSites
if Conf[NewActive] == 0: Conf[Active], Conf[NewActive] = 0, 1
PP = '|'
ktot= 0
for k in range(NSites):
if Conf[k] == 0:
PP += ' '
else:
ktot += 1
if ktot != NPart / 2: PP += 'X'
else: PP += '|'
if iter % NStrob == 0: print(PP)
print('-' * (NSites + 2))
Text = 'Total time = ' + str(prefactor) + ' * N ^ ' + str(exponent) + ' * log N'
print(' ' * (NSites// 2 + 1 - len(Text) // 2) + Text + ' ' * (NSites// 2 + 1 - len(Text) // 2))
This example program performs a large number of iterations of the Monte Carlo algorithm for the Symmetric Simple Exclusion Process, and plots 40 lines of output over the entire simulation time.
Output
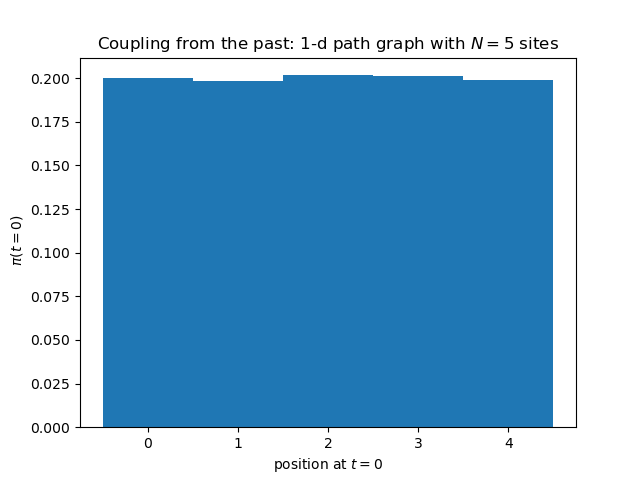
Here is output of the above Python program. The histogram is absolutely flat, without any corrections. But this is normal, given that the simulation has run, for each of the realizations of the random map, an infinite number of iterations.