From Werner KRAUTH

S. Piatecki and W. Krauth Efimov-driven phase transitions of the unitary Bose gas arXiv 1307.4671

Contents 1 Paper 2 Illustration

Paper

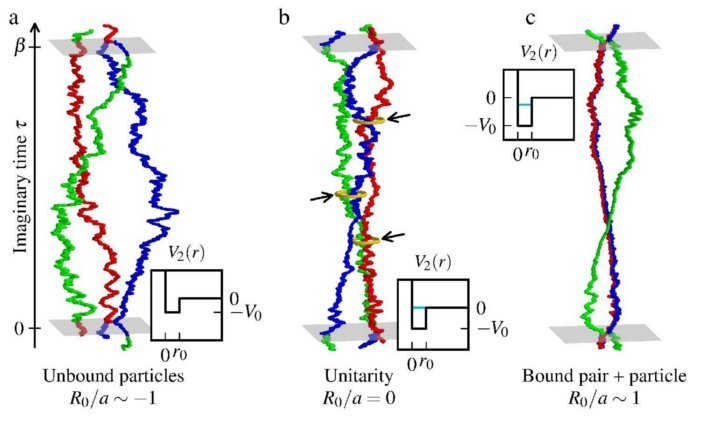
Abstract In quantum physics, Efimov trimers are bound states of three particles that fall apart like Borromean rings when one of them is removed. Initially predicted in nuclear physics, these striking bosonic states are hard to observe, but the "unitary" interactions at which they form is commonly realized in current cold atoms experiments. There, they set the stage for a new class of universal physics: Two-body interactions are all but invisible, but three-body effects allow the emergence of a largely uncharted new world of many-particle bound states. Three-particle systems were characterized theoretically, and the ground-state properties of small unitary clusters computed numerically, but the macroscopic many-body behaviour has remained unknown. Here we show, using a Path-Integral Monte Carlo algorithm backed up by theoretical arguments, that the unitary Bose gas presents a first-order phase transition from a normal gas to a superfluid Efimov liquid. The normal gas is very well described by the available virial coefficients. At unitarity, the phase diagram of the bosonic system is universal in rescaled pressure and temperature. A triple point separates the normal gas, the superfluid Efimov liquid, and a third phase, the conventional superfluid gas. These two superfluid phases are separated by a critical line that ends in a critical point at high temperature. This rich phase diagram should allow for a number of experimental protocols that would probe these universal transitions between the normal gas, the superfluid gas, and the superfluid Efimov liquid.

Electronic version (from arXiv, original version)

Supplementary information (from arXiv, original version)

Illustration

Here you see three bosons, in path integral representation, and with a certain pseudopotential interaction that is described in more detail in the paper. On the left side, the particles are slightly repulsive, on the right side, they are attractive (so that two particles simple get together and bind into a dimer, whereas the third particle just sits around. In the center, you see the particles at the unitary point: pair interactions are very weak, so pairs get together, but unbind. After a little while, another pair forms, etc etc. The final outcome is that ensembles of two particles fall apart, but three particles stay together, just like Borromean rings...