Bernard Krauth Wilson 2009
From Werner KRAUTH
E. P. Bernard, W. Krauth, D. B. Wilson Event-chain algorithms for hard-sphere systems Physical Review E 80 056704 (2009)
Contents |
Paper
Description: In this paper, we first presented the event-chain algorithm, a fast irreversible Markov-chain (initially) for hard spheres and related systems. In a single move of these rejection-free methods, an arbitrarily long chain of particles is displaced, and long-range coherent motion can be induced. Numerical simulations initially showed that event-chain algorithms outperform the conventional Metropolis method. The method violates detailed balance but satisfied a global-balance conditions.
Further information: We used this algorithm, which is about 100 times faster than the local Metropolis algorithm, for our work on the liquid-hexatic transition in two-dimensional hard disks. See my 2011 paper, with Etienne Bernard, for the generalization of the event-chain algorithm to general, continuous, potentials.
This algorithm can be generalized to arbitrary interaction potentials. A first version was presented in a paper with Etienne Bernard, but the definitive method was worked out in collaboration with Manon Michel and Sebastian Kapfer, in 2014.
Much further research was dedicated to analyzing event-chain Monte Carlo. In [[Kapfer Krauth 2017a| later works, with Sebastian Kapfer], we showed that, in one dimensional models (which can be analyzed more fully), ECMC has much better scaling with the system size than regular Monte Carlo. This was even [[Lei Krauth 2018| proven mathematically] in a special case, together with Ze Lei.
Electronic version (from arXiv)
Published version in Physical Review E (subscription required)
Illustration
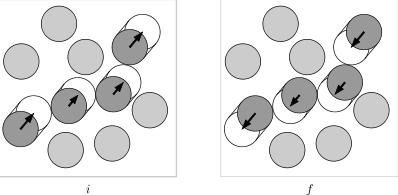
Here is the basic schema of the event-chain algorithm (the added length of the arrows equals a fixed value l. The event-chain algorithm is microreversible and it has no rejections. In our applications, we use a version of the algorithm where particles moveeither in the +x or the +y direction. This is also done in the below Python implementation.
Python Implementation
Here is a basic python implementation of the straight event-chain algorithm for four disks in the version breaking detailed balance. A randomly disk always moves in the +x direction. At each step, the configuration is translated (and flipped) so that the moves starts at <math>(x,y)=(0.,0.)</math>.
###========+=========+=========+=========+=========+=========+=========+=
## PROGRAM : event_chain.py
## TYPE : Python script (python 2.7)
## PURPOSE : Event-chain simulation for 4 particles in a square box
## with periodic boundary conditions.
## COMMENT : L is a list of tuples, move is always in +x direction
## Flip_conf exchanges x and y (effective move in +y direction)
## VERSION : 10 NOV 2011
##========+=========+=========+=========+=========+=========+=========+
from random import uniform, randint, choice, seed
import math, pylab, sys, cPickle
def dist(x,y):
"""periodic distance between two two-dimensional points x and y"""
d_x= abs(x[0]-y[0])%box
d_x = min(d_x,box-d_x)
d_y= abs(x[1]-y[1])%box
d_y = min(d_y,box-d_y)
return math.sqrt(d_x**2 + d_y**2)
def Flip_conf(L,rot):
L_flip = []
for (a,b) in L:
if rot == 1: L_flip.append((box - b,a))
else: L_flip.append((b,box - a))
return L_flip,-rot
#=========================== main program starts here =========================================
box = 4.0
data = []
L = [(1.,1.),(2.,2.),(3.,3.),(3.,1.)] # initial condition
rot = 1
ltilde = 0.9
for iter in xrange(1000000):
if iter%10000 == 0: print iter
i = randint(0,3)
j = (i + randint(1,3))%4
data.append(dist(L[i],L[j]))
if randint(0,1) < 1: L,rot = Flip_conf(L,rot)
Zero_distance_to_go = ltilde
next_particle = choice(L)
while Zero_distance_to_go > 0.0:
#
# this iteration will stop when the Zero_distance_to_go falls to zero
#
L.remove(next_particle)
L = [((x[0]-next_particle[0])%box,(x[1]-next_particle[1])%box) for x in L]
next_position,next_particle = (float("inf"),(float("inf"),0.0))
Current_position = 0.0
for x in L:
x_image = list(x)
if x[0]> box/2: x_image[0] = x[0] - box
if x[1]> box/2: x_image[1] = x[1] - box
if abs(x_image[1]) < 1.0:
x_dummy = x_image[0] - math.sqrt(1.0 - x_image[1]**2)
if x_dummy > 0.0 and x_dummy < min(Zero_distance_to_go,next_position):
next_position,next_particle = (x_dummy,x)
distance_to_next_event = next_position - Current_position
if Zero_distance_to_go < distance_to_next_event:
Current_position += Zero_distance_to_go
L.append((Current_position,0.0))
break
else:
Current_position += distance_to_next_event
Zero_distance_to_go -= distance_to_next_event
L.append((Current_position,0.0))
pylab.hist(data,bins=40,normed=True,alpha=0.5,cumulative=True)
pylab.title("Event chain for four hard disks, l = "+str(ltilde))
pylab.xlabel("Periodic pair distance $r_{ij}$")
pylab.ylabel("Integrated probabilities $\Pi(r_{ij})$")
pylab.savefig('Event_chain'+str(ltilde)+'.png')
pylab.show()
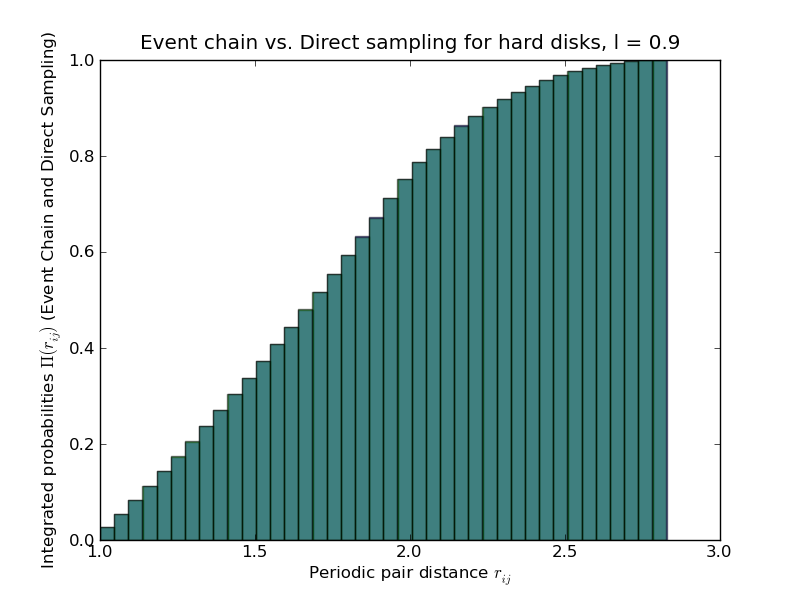
Comparison of output with direct-sampling algorithm
Here is a comparison between the event-chain algorithm and a perfect-sampling approach for four disks of size 1/2 in an <math>L\times L</math> square box of length <math>L=4</math>.