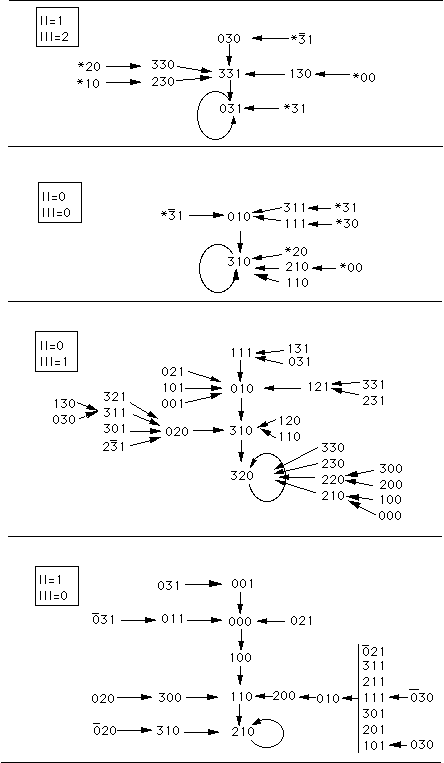
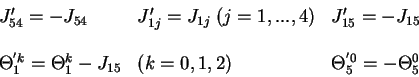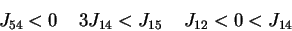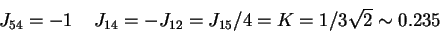Figure 7. Iteration graphs for the solution with five linear automata when
J54
> 0 and
J15
< 0 (the network on Figure 6 b). The states of automata II and III which
are independent of the other automata, are indicated at the upper left corners
of the 4 graphs. Each configuration of the network is then specified by the
states of automata I, IV and V which are figured in a 3 digits representation.
The first digit gives the state of automaton I, the second of automaton IV and
the third of automaton V. The * symbol indicate any of the four states 0,1,2,3,
and the bar above a digit means all digits except this one (
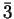 = {0,1,2};
= {0,1,2};
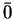 =
{1,2,3}). The arrows indicate transitions from one configuration to the next one.
=
{1,2,3}). The arrows indicate transitions from one configuration to the next one.
6.
Biological interpretation
The
method of analysis presented here allowed us to build up some of the simplest
mathematical models that account for the observed experimental behavior. Most
of the arbitrariness of the modelling is removed by the search for simplicity
(cancelling of the connections, the sign of which is not fixed by the field
inequalities) and for the most stable solution.
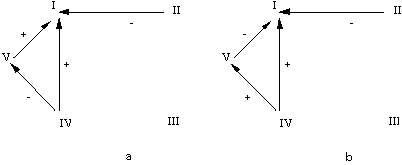
From
a biological point of view, figs. 2, 5
and 6 show that the growth factors
produce a direct inhibition of the two ion transporters accompanied by a much
stronger indirect stimulation of the OS
Na+K+
pump mediated by the activation of the adenylate cyclase dependent cAMP second
messenger system. In addition, figs. 5 and 6
represent two different
alternatives for a complex coupling pattern between the two ion transporters.
In both cases, we are dealing with a double coupling: a direct, reciprocal
positive one, whereby the activation of one of the transporters triggers the
activation of the other and an indirect negative unidirectional one, whereby
the activation of the OS
Na+K+
pump produces an inhibition of the BS transporter.
-
The former effect can be easily interpreted as the result of the changes in
intracellular
Na+
concentrations produced by the activation or inhibition of each of the
transporters. The OS transporter pumps out
Na+
from the cell whereas the BS transporter facilitates the entry of
Na+
into the cell. Both are very sensitive to changes in intracellular
Na+
concentration because of its normal very low value (of the order of 0.5 M).
Therefore, any change in intracellular
Na+
produced by the activation of one of the transporters will produce a negative
feedback by means of the activation of the other.
-
The later effect can be produced by two different, non mutually exclusive
mechanisms, which can be given different interpretations in terms of molecular
interactions. In Figure 5, the assumed second order interaction means that the
inhibitory effect of the OS pump on the BS transporter is dependent on the
activation of the cAMP synthesis. Such an effect suggests a direct bimolecular
reaction involving the two transporters. Contrary to the OS
Na+K+
ATPase, the molecular structure responsible for the BS cotransport system has
not yet been isolated. Therefore, the hypothesis of a direct interaction
between the two (or three) molecular structures cannot be tested directly. On
the other hand, the apparent difficulty in isolating and purifying a specific
membrane protein proven to have the function of the BS transporter in intact
membranes, may indicate that the function of this transporter cannot be easily
separated from that of other membrane components. In Figure 6,
the inhibitory effect of OS
Na+K+
pump on the BS transporter is mediated by a so-called "hidden" component. In
fact, based on data from different cellular systems, it is easy to guess what
this component is likely to be. Studies on mouse and human fibroblasts (Panet
& Atlan, 1990; Snyder et al, 1991a,b) have shown that some effects of
growth factors on the BS transporter are mediated by their effect on the
Inositol 3 Phosphate and
Ca++
dependent second messenger system. Furthermore, a stimulating or inhibiting
effect is observed depending on the physiological state of the cell (completely
arrested or not) and on the nature of the
Ca++
dependent second messenger pathway (Protein kinase C dependent or independent)
activated by different growth factors tested separately.
In
any case, the fact that the transporters and receptor system can be modelled by
a set of 4 or 5 components does not imply that the set of chemicals involved in
the regulation of the response is limited to so few components. Each of the
couplings indicated by an arrow is only a phenomenological representation which
can be mediated by several reactions involving many chemicals. However, the
modeling technique provides for a simple minimum model which allows to make
sense of otherwise entangled uninterpretable data.
Acknowledgments.
The Laboratoire de Physique Statistique is supported by CNRS (URA 1306). We
acknowledge financial support from INSERM grant 879002.
References
Alkon, D. L. & Rasmussen, H. (1988), A spacial temporal model of cell
activation. Science
239,
998-1004.
Anlauf
J. K. & Biehl M. 1989 "The adatron: an adaptative perceptron
algorithm" Europhys. Lett.
10
687
Atlan,
H., Panet, R., Sidoroff, S., Salomon, J. & Weisbuch, G. (1979), Coupling of
ionic transports and metabolic reactions in rabbit reticulocytes. Bond Graph
Representation. J. Franklin Institute
308
(3), 297-308.
Berridge,
M. (1986). In:
Calcium
and the Cell
(Evered, D. & Whelan, J., eds) pp. 39-57, Chichester: Wiley.
Bourrit,
A., Atlan, H., Fromer, I., Melmed, R. N. &Lichstein, D. (1985), Basic
characterization of an ouabain-resistant, bumetadine-sensitive K+
carrier-mediated tranport system in J774.2 mousse macrophage-like cell line and
in variants deficient in adelylate cyclase and cAMP-dependent protein kinase
activities, Biochim. Biophys. Acta
817,
85-94.
Duda
R. O. and Hart P. E. (1973)
Pattern
classification and scene analysis
(New-York, Wiley)
Holcombe, W. M. L. (1982).
Algebric
Automata Theory
:
Cambridge, England: Cambridge University Press
Hertz J., Krogh A. and Palmer D. (1990),
Introduction to the theory of Neural Computation
,
Lectures notes in Santa Fe series on Complexity, Addison Wesley.
Kauffman
S., (1969), Metabolic stability and epigenesis in randomly constructed genetic
nets, J. Theo.Biology
22,
437-467.
Krauth
W. and Mézard M. 1987 " Learning algorithms with optimal stability in
neural networks", J Phys A: Math Gen
20
L745
Le
Cun Y. 1985 "A learning scheme for asymmetric threshold networks", in
Cognitiva, (CESTA-AFCET Ed.), pp. 599-604
Lichstein,
D. & Atlan, H. (1990), The "cellular state" : the way to regain specificity
and diversity in hormone action, J. Theor. Biol
145,
287- 294.
Mickulecky, D. C. (1977), A simple network thermodynamic method for
series-parallel coupled flows, J. Theor. Biol.
69,
511-541.
Nabutovsky
D. and Domany E. (1991) "Learning the unlearnable", Neural
Computation 605-616
Minsky
M and Papert S, 1969
Perceptrons
(MIT Press, Cambridge, MA)
Oster,
G. F., Perelson, A. S. & Katchalsky, A. (1973), Network thermodynamics :
dynamic modelling of biophysical systems, Q. Rev. Biophys.
6(I),
1-134.
Panet,
R., Amir, I. & Atlan, H. (1986a), Fibroblast growth factor induces a
trasient net K+ influx carrier by the bumetadine-sensitive transporter in
quiescent BALB/c 3T3 fibroblasts, Biochim. Biophys. Acta
859,
1117-1121.
Panet,
R., Snyder, D. & Atlan, H. (1986b), Amiloride added together with
bumetadine completely blocks mouse 3T3 cell exit from GO/G1 phase entry into
S-phase, Biochem. J.
239,
745-750.
Panet, R. & Atlan, H. (1990), Bumetadine-sensitive Na+/K+/Cl- transporter
is stimulated by Phorbol Ester and different mitogens in quiescent human skin
fibroblasts, J. Cell. Physiol.
145,
30-38.
Panet,
R. & Atlan, H. (1991), Stimulation of Bumetadine-sensitive Na+/K+/Cl-
Cotransport by different mitogens in synchronized human skin fibroblasts is
essential for cell proliferation, J. Cell. Biol., in press.
Paris,
S. & Pouyssegur, J. (1986),Growth factor activate the bumetadine-sensitive
Na/K/Cl Cotransport in hamster fibroblasts, J. Biol. Chem.
261(14),
6177-6183.
Pouyssegur,
J., Chambard, J. C., Franchi, A., Paris, S. & Van Obberghen-Schilling, E.
(1982), Growth factor activation of an amiloride-sensitive Na+/H+ exchange
system in quiescent fibroblasts : coupling to ribosomal protein S6
phosphorilation, Proc. Natn. Acad. Sci U.S.A.
79,
3935-3939.
Rapp,
P. E. & Berridge, M. J. (1977), Oscillations in Calcium-Cyclic AMP control
loops form the basis of pacemaker activity and other higgh frequency biological
rhythms, J. Theor. Biol
66
,
497-525.
Rujan
P. (1991), A fast method for calculating the perceptron with maximal stability,
preprint
Rumelhart
D.E., Hinton G.E., Williams R.J. 1986 "Learning internal representations by
error propagation", in
Parallel
Distributed Processing
,
Rumelhart and McClelland Ed. (Bradford Books, Cambridge MA, 1986) Vol.1
Snyder, D., Markus, M., Atlan, H. & Panet, R. (1991a), The Phorbol
ester TPA inhibits the stimulation of Bumetadine-sensitive Na+/K+/Cl-
transporter by different mitogens in quiescent BALB/C 3T3 mouse fibroblasts ,
J. Cell. Physiol.
146,
406-472.
Snyder, D., Atlan, H., Markus, M. & Panet, R. (1991b), Na+/K+/Cl-
Cotransport is stimulated by a Ca++ -Calmoduline- mediated pathway in
BALB/c 3T3 fibroblasts J. Cell. Physiol
149,
pp 497-502
Thomas
R. (1975),
Kinetic
Logic
,
Lectures notes in Biomathematics vol. 29, Springer Verlag.
Thomas
R. and D'Ari, R. (1990),
Biological
Feedback
,
Boca Raton Fl., CRC.
Weisbuch
G., (1991)
Complex
systems dynamics
,
Lectures notes in Santa Fe series on Complexity, Addison Wesley.
[*]
Service de Biophysique, Faculté de Médecine Broussais Hotel-Dieu,
15 rue de l'Ecole de Médecine, F- 75006 Paris; present address: Medical
Biophysics, Hadassah University Hospital, Jerusalem, Israel.
[+]
Laboratoire associé au C.N.R.S. (URA 1306) et aux Universités
Paris VI et Paris VII
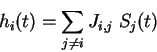
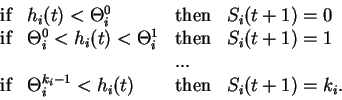
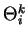 .
The interaction strength
and
the thresholds should be compatible with equations (2) when the automaton
states are given the experimentally observed quantities written in Table 1 for
the N=4 automata: these data tell us that 12 particular configurations of
states
.
The interaction strength
and
the thresholds should be compatible with equations (2) when the automaton
states are given the experimentally observed quantities written in Table 1 for
the N=4 automata: these data tell us that 12 particular configurations of
states
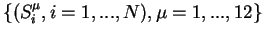 are fixed points of the dynamics (2). The compatibility conditions are a set of
inequalities which are explicitly given in the next sections.
are fixed points of the dynamics (2). The compatibility conditions are a set of
inequalities which are explicitly given in the next sections.
 on i. In general, one expects for
each set either no solution or an infinite number of solutions.
on i. In general, one expects for
each set either no solution or an infinite number of solutions.
![[figure 1]](figures/fig1.jpg)
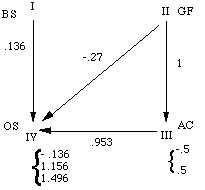
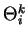 (after brackets) describing automata II, III and IV.
(after brackets) describing automata II, III and IV.
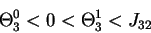
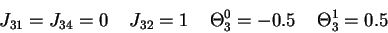
![[figure 3]](figures/fig3.gif)
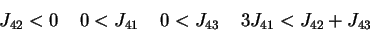
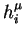 and
and
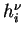 which correspond to two different level of activity (say
which correspond to two different level of activity (say
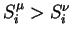 ), are as different as possible (
), are as different as possible (
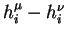 is to be maximized). The best solution is the one which maximizes the
smallest difference among all couples
is to be maximized). The best solution is the one which maximizes the
smallest difference among all couples
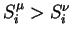 (and it is of course sufficient to consider only couples
(and it is of course sufficient to consider only couples
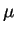 ,
,
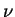 with
with
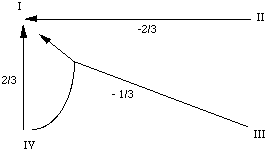
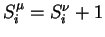 . In the case of automaton IV, among the 9 differences that can be written
(see Figure 3), 6 can be shown to be implied by the 3 others. We then have to
maximize
. In the case of automaton IV, among the 9 differences that can be written
(see Figure 3), 6 can be shown to be implied by the 3 others. We then have to
maximize
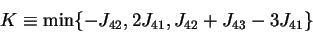
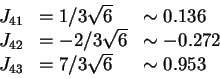
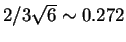 . The thresholds are set in the middle of the
segment joining two closest fields:
. The thresholds are set in the middle of the
segment joining two closest fields:
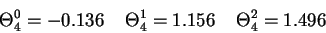
![[figure 4]](figures/fig4.gif)
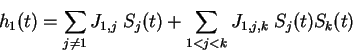
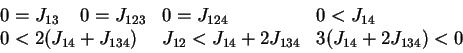
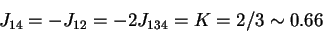
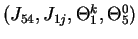 ,
then a solution
,
then a solution
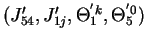 is derived for 6b as follows:
is derived for 6b as follows: