Automates cellulaires à deux dimensions

Les automates cellulaires à deux dimensions ont une histoire relativement ancienne, de l'automate autoreproducteur de von Neumann qui date des années quarante, en passant par le "jeu de la vie" dû à Conway (1960). La faculté de suivre le mécanisme des interactions entre les automates et la possibilité d'observer l'état du réseau à un instant donné de l'itération en font des instruments de modélisation précieux .

En deux dimensions, la structure des connexions est liée aux symétries du réseau, déjà répertoriées par les cristallographes: dans la mesure où l'on exige que le réseau ait à la fois une symétrie de translation et une symétrie de rotation autour de chacun de ses noeuds, la symétrie de rotation ne peut être que d'ordre 2, 3, 4 ou 6. On étudie donc des réseaux triangulaires (chaque automate possède six voisins immédiats), carrés (quatre voisins) et hexagonaux (trois voisins) (Fig. 4.1).

Figure 4.1. Réseau carré. Réseau triangulaire. Réseau hexagonal.

Nous parlerons surtout de réseaux à maille carrée, ou réseaux carrés. Deux types de connectivité plus ou moins étendue sont principalement étudiés. Dans le voisinage de von Neumann, chaque automate a cinq entrées: lui-même plus ses quatre voisins. Dans le voisinage de Moore, il en a neuf: lui-même plus ses huit plus proches voisins (Fig. 4.2).

Figure 4.2 Voisinage de von Neumann. Voisinage de Moore. Il existe une abondante littérature sur les propriétés de ces réseaux. Nous ne parlerons que d'un modèle simple de la croissance cristalline, fondé sur les automates à compteurs, et , plus brièvement, le jeu de la vie de Conway. Pour plus de variété, le lecteur pourra se reporter à l'imposante compilation de S. Wolfram: Theory and Applications of Cellular Automata, World Scientific (1986).

4-1 Compteurs et croissance

Avec des voisinages aussi importants (k = 5 ou 9), il n'est pas question d'entreprendre une étude exhaustive de l'ensemble des automates booléens. Comme dans le cas des automates cellulaires à une dimension, on s'intéresse aux règles de transition qui conservent les symétries du voisinage. C'est le cas des règles à compteurs pour lesquelles la fonction de transition ne dépend que de la somme des états du voisinage.

Pour les automates à seuil, on définit un seuil, entier ou réel, compris entre -1 et k+1, où k est la connectivité d'entrée de l'automate. La somme des états des voisins est évaluée et comparée au seuil: le nouvel état de l'automate est 1 si cette somme est supérieure ou égale au seuil, 0 sinon.

Sur un réseau cellulaire, les seuils faibles (c'est-à-dire négatifs ou proches de 0) favorisent la croissance de zones d'automates dans l'état 1, tandis que les seuils forts (proches de k) favorisent celle de zones d'automates dans l'état 0.

Suivons par exemple l'évolution des comportements dynamiques lorsque le seuil augmente. Nous nous limiterons aux réseaux carrés et au voisinage de von Neumann (5 entrées), mais tous les résultats que nous énoncerons s'étendent sans difficultés aux autres cas de figure. Pour les seuils négatifs, en une seule itération le réseau est recouvert de 1. Si le seuil est positif mais inférieur ou égal à 1, la présence d'automates à l'état 1 (les germes) permet la croissance de zones à l'état 1 au voisinage de ces germes. En l'absence de germes, il n'y a pas de croissance.

Les phénomènes les plus intéressants se produisent pour les valeurs intermédiaires du seuil. Pour un seuil compris entre 1 et 2, la condition de croissance correspond à la présence d'au moins deux voisins à l'état 1. Les amas de 1 sont encore favorisés mais les 1 isolés sont détruits. Les germes doivent compter au moins trois automates voisins non alignés à l'état 1. La croissance ne se produit qu'à la lisière des facettes (Fig. 4.3 et 4.4).

t = 0 t = 1 t = 2 t = 3 t = 4

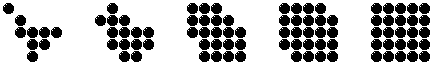
Figure 4.3 Evolution de quelques configurations simples pour des automates cellulaires de seuil 1,5. Le point isolé disparaît, la paire horizontale est fixe, et la paire en diagonale oscille avec une période 2. Le triplet en coin évolue en un coup vers un carré stable de quatre automates. Si les amas de 1 sont assez dispersés, la croissance s'arrête lorsque l'enveloppe convexe des configurations initiales est remplie de 1.

t = 0 t = 1 t = 2 t = 3 t = 4

Figure 4.4 Croissance par les facettes d'un cristal à partir d'un germe (automates cellulaires de seuil 1,5). Ce mode de croissance représente assez bien la croissance des cristaux à l'équilibre thermodynamique, c'est-à-dire lorsque le refroidissement du bain est suffisamment lent. C'est le cas de cristaux minéraux réguliers, comme par exemple le quartz. L'enveloppe convexe des germes correspond aux formes d'équilibre. La croissance se fait par les facettes, mais de temps en temps une impureté, une irrégularité du réseau ou même un atome isolé "collé" sur la facette permettent la croissance d'une nouvelle rangée d'atomes sur cette facette. Dans les systèmes physiques, ce sont ces irrégularités dues aux imperfections du cristal ou à l'agitation thermique qui permettent que la croissance se poursuive des germes microscopiques aux beaux cristaux macroscopiques.

Pour un seuil compris entre 2 et 3, il n'y a pas de croissance le long des facettes; celles-ci sont au contraire "décapées" de tous leurs atomes isolés. Pour les seuils plus élevés, le rôle des 0 et des 1 est inversé, et l'on observe dans l'ordre inverse les phases de croissance des zones de 0.

Pour d'autres voisinages et d'autres réseaux, on obtient des comportements semblables, mais pour des seuils éventuellement différents. La forme des cristaux peut, elle aussi, être modifiée: on obtient alors des cristaux en losange ou en hexagone.

4-2 Automates a fenêtre et croissance dendritique On peut observer dans la nature d'autres formes de cristaux: le cas des cristaux de neige est un exemple de croissance dendritique qui produit des formes très découpées. Ce type de croissance se produit lorsque le germe solide est nettement plus froid que la solution. Dans ce cas, la difficulté d'évacuer la chaleur de cristallisation favorise la croissance de dendrites qui vont chercher assez loin les zones froides du liquide. Il est possible de modéliser cette croissance par des automates cellulaires, à condition d'exclure la transition vers l'état 1 lorsque le nombre de voisins à l'état 1 est trop grand, pour tenir compte du problème d'évacuation de la chaleur de cristallisation. On utilise alors des automates "à fenêtre". L'état d'un tel automate ne passe à 1 que si le nombre de ses voisins à 1 n'est ni trop grand ni trop petit. Dans le cas du voisinage de von Neumann, la règle suivante permet la croissance de la structure dendritique représentée sur la figure 4.5:

Si un automate est à 1, il y reste.

Si un automate est à 0, il ne passe à 1 que si le nombre de ses voisins à 1 est égal à 1.

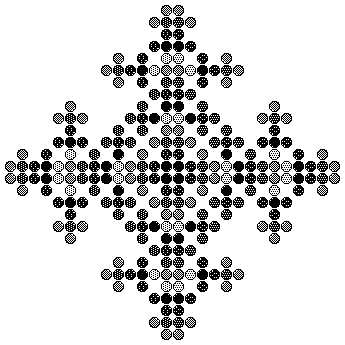
Figure 4.5 Automates à fenêtre et croissance dendritique. Cette figure est obtenue après 13 itérations à partir du germe carré des 4 automates au centre de la figure. Les différentes teintes de boules correspondent aux étapes successives de l'itération (les boules noires correspondent par exemple aux étapes 0, 5 et 10). 4-3 Le "jeu de la vie" de Conway

Le jeu de la vie est basé sur un automate cellulaire très simple dont la diversité des comportements dynamiques en fonction des configurations initiales est étonnante. Cette dynamique très riche en a fait une vedette des récréations mathématiques et des programmes élémentaires d'initiation à l'informatique. Les motivations de son auteur, Conway, rappellent un peu celles de von Neumann. Nous n'exposons pas le modèle de l'automate autoreproducteur de von Neumann à cause de sa complexité: c'est un automate à 29 états, et la configuration constructrice comprend 200 000 automates à l'état non quiescent. Par contre, celui de Conway est beaucoup plus simple. Le voisinage est celui de Moore (neuf entrées). Voici les règles de transition:

* Un automate à l'état 0 passe à l'état 1 si trois de ses voisins sont à l'état 1 ("il naît"). Sinon il reste à 0.

* Un automate à l'état 1 reste à l'état 1 si deux ou trois de ses voisins sont à l'état 1. Il passe à 0 dans les autres cas. (Il "meurt", soit d'isolement, soit d'étouffement.)

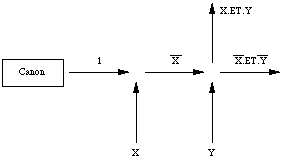
 La figure 4.6 montre l'évolution de quelques configurations simples. Le lecteur pourra s'amuser à suivre à la main sur du papier quadrillé, ou à programmer, l'évolution d'autres configurations. En général, la plupart des configurations évoluent assez rapidement vers un ensemble de configurations attractrices simples: carrés, nids d'abeille, feux clignotants.

La configuration du planeur est assez remarquable: on la retrouve identique à elle-même, à une translation près, après quatre itérations. C'est l'un des ingrédients de base pour la construction d'un véritable "ordinateur cellulaire". Avant d'indiquer les principes de base de cette construction, donnons-en les motivations. Une manière d'étalonner la richesse des comportements dynamiques d'un système consiste à démontrer son équivalence formelle avec une machine de Turing, ou calculateur universel, dont les performances sont bien établies. Pour construire une machine de Turing il suffit de savoir construire deux fonctions logiques, dont la négation. Notre ordinateur cellulaire est donc basé sur les éléments suivants:

* Les planeurs, jouant le rôle d'un signal binaire se propageant à vitesse constante le long de diagonales du réseau. La présence d'un planeur s'interprète comme un signal 1, son absence comme un 0.

* La configuration "canon" expulse des planeurs à intervalles réguliers (toutes les trente itérations). Grâce à elle nous disposons d'un signal à l'état 1.

* La collision de deux planeurs les détruit tous les deux.
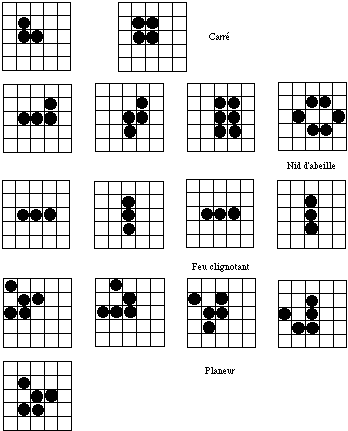
Figure 4.6 Le "jeu de la vie" de Conway. Evolution de quatre configurations. Le temps varie de gauche à droite. Les deux premières configurations évoluent vers des points fixes, la troisième vers un attracteur de période deux; la quatrième est un planeur, qui se reproduit identique à lui-même à une translation d'un carreau près (vers le bas et vers la droite), après quatre itérations. La figure 4.7 donne un exemple de réalisation de fonctions logiques.

La combinaison de fonctions logiques de deux types différents (par exemple ET et NEGATION) permet la construction d'une machine de Turing, de même que la combinaison de circuits intégrés (inverseur et ET) permet la réalisation pratique d'un ordinateur. Bien entendu, personne ne songerait à réaliser un ordinateur à partir d'automates de Conway; toute cette discussion n'a pour but que de démontrer la richesse des comportements observables avec le "jeu de la vie".

Figure 4.7 Configurations du jeu de la vie et fonctions logiques. A partir de la configuration canon qui émet des planeurs toutes les 30 itérations, on peut réaliser, sur les axes de propagation du signal figurés ici par les flèches, les fonctions logiques négation () (X), X.ET.Y, .ET., des signaux d'entrée X et Y, représentés par la présence ou l'absence de planeurs. En combinant de cette manière des fonction logiques élémentaires, on peut réaliser un calculateur universel.

Références

Outre le livre de S.Wolfram, Theory and Applications of Cellular Automata déjà cité, l'article de G. Vichniac "Cellular Automata Models of Disorder and Organization", dans Disordered Systems and Biological Organization, édité par E. Bienenstock, F. Fogelman-Soulié et G. Weisbuch, (Springer, 1986), développe les problèmes abordés dans la première partie de ce chapitre.

Le "jeu de la vie" est exposé en détail par J. Conway dans le chapitre 25 de Winning Ways, vol.2, édité par E. Berkelamp, J. Conway et R. Guy (Academic Press, 1982).