Chapitre 7
Des cellules cachées
Classifications
On peut dire d'un réseau de Hopfield qu'il classe des configurations suivant leur bassin d'attraction: deux configurations sont équivalentes si elles ont le même attracteur. Nous avons vu qu'en fait cette classification est basée sur un critère de voisinage au sens de la distance de Hamming. En fait, ce critère, intéressant dans certains cas, n'est pas forcément pertinent dans d'autres. Dans le domaine de la reconnaissance des formes, par exemple, on s'intéresse plutôt aux invariances: nous considérons deux formes comme équivalentes si elles se déduisent l'une de l'autre par translation. Or, dans ce cas, la distance de Hamming des deux patterns peut très bien être importante.
Nous nous proposons dans ce chapitre de préciser la nature des classifications susceptibles d'être effectuées et apprises par les réseaux de Hopfield et les réseaux équivalents. Puis nous tenterons de proposer d'autres types de réseaux permettant de résoudre les problèmes que ne résolvent pas les réseaux de Hopfield.
7-1 LE PERCEPTRON
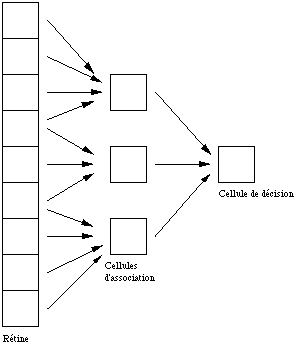
En fait, les possibilités de discrimination des réseaux de Hopfield sont équivalentes à celles du perceptron, une machine vieille déjà de plus de vingt ans. Dans sa version la plus simple, le perceptron est un réseau composé de trois couches:
• La première couche, appelée rétine, est celle des cellules d'entrée, sur lesquelles sont appliqués les patterns à classer.
• La deuxième couche est constituée de cellules associatives, par exemple des automates booléens dont les entrées sont prises parmi les cellules de la rétine. Leurs fonctions booléennes, variant éventuellement d'un automate à l'autre, sont fixées au départ: elles ne sont pas susceptibles d'apprentissage.
• La dernière couche comprend une ou plusieurs cellules de décision, qui sont en fait des automates à seuil dont les poids sont modifiés lors de la procédure d'apprentissage (Fig. 7.1).

Figure 7.1
Le réseau n'a pas de boucles: l'information est donc traitée en un seul passage à travers les couches successives. Il n'y a pas de dynamique itérative vers un attracteur comme dans les exemples que nous avons traités jusqu'ici.
Les classificateurs linéaires
Raisonnons tout d'abord sur une seule cellule de décision. Cette cellule calcule une fonction de décision F définie par les poids synaptiques Tj et les fonctions booléennes fj des cellules d'association j suivant
![]()
![]()
où s représente le pattern d'entrée, Y la fonction de Heaviside et Q le seuil. Nous pouvons ainsi définir deux classes sur les patterns d'entrée, dont l'une est composée des patterns tels que la fonction F donne 1.
Le premier point à remarquer est que le perceptron est un classificateur linéaire. En effet, l'espace des configurations fi(s) est divisé en deux par l'hyperplan défini par les Tj et le seuil. Une seule cellule de décision ne pourra jamais que séparer des ensembles situés de part et d'autre d'un hyperplan. Bien entendu, en augmentant le nombre des cellules de décision, on peut affiner la sélection. Les hyperplans séparent, dans l'espace des configurations, des polytopes dont chacun correspond à une classe possible.
Les réseaux de Hopfield sont basés essentiellement sur les mêmes critères de stabilité que les perceptrons. La règle de calcul du perceptron:
![]()
![]()
est essentiellement la formule de stabilité donnée au chapitre 5 pour le système de Hopfield. Les systèmes de Hopfield sont donc eux aussi des classificateurs linéaires et ils en ont donc les limites. Avant de poursuivre notre discussion sur les limites des classificateurs linéaires, rappelons un résultat intéressant obtenu pour le perceptron.
Le théorème de convergence
Nous avons déjà parlé au chapitre 6 de l'algorithme d'apprentissage du perceptron. Rappelons-le ici dans la formulation adaptée au perceptron. On utilise la représentation -1, +1 pour la cellule de décision. Le signal de sortie observé est donc S = 2 F -1. Soit y la sortie observée lors de la présentation d'un pattern. On part d'un vecteur de poids synaptiques aléatoires. A chaque présentation, on ne modifie les poids synaptiques que si y et S diffèrent. On applique alors la formule:
Tj –> Tj + (y - S) fj(s) (7.3)
Le seuil lui aussi est modifié par le même algorithme. Il s'introduit simplement en créant une cellule d'association supplémentaire sans input, dont l'état est toujours maintenu à -1. Q est tout simplement le poids synaptique de cette cellule.
Le théorème de convergence du perceptron assure que s'il existe une fonction réalisant la classification choisie, alors l'algorithme converge en un temps fini vers une fonction F satisfaisante.
Un contre-exemple simple
A ce stade, il devient intéressant de préciser ce que ne peuvent pas faire les classificateurs linéaires. Les problèmes apparaissent si on essaie de regrouper des configurations séparées par les hyperplans. Prenons le cas où l'on souhaiterait implémenter la fonction OU exclusif (OUex) pour deux cellules. En deux dimensions, l'espace des configurations est le plan, et le séparateur linéaire la droite d'équation:
T1 x + T2 y = Q (7.4)
où x est l'état de la cellule 1 et y celui de la cellule 2.
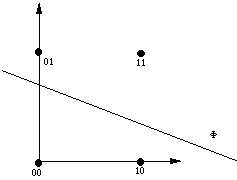
Figure 7.2
Cette représentation géométrique montre bien l'impossibilité de réaliser la fonction OUex qui regrouperait les configurations 01 et 10 (Fig. 7.2). Or cette fonction assure justement la détection d'un seul 1 dans le pattern, indépendamment de sa position sur la première ou la deuxième cellule. D'où son importance en tant que modèle de reconnaissance invariante.
On pourrait certes confier la tâche d'assurer les fonctions de type OUex aux cellules d'association. Toutefois ces cellules ne sont pas capables d'apprendre. Autrement dit, en faisant ce choix, on abandonnerait l'idée d'apprendre en n'utilisant que les exemples fournis.
Nous savons cependant, depuis les travaux de McCulloch et Pitts, qu'un réseau d'automates à seuil est capable d'implémenter la fonction OUex. La figure 7.3 en donne un exemple.
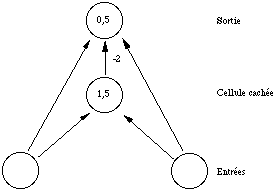
Figure 7.3
Deux automates à seuil permettent d'implémenter la fonction OUex. Les flèches représentent des connexions de poids synaptique 1, sauf la flèche verticale d'intensité -2. Les chiffres à l'intérieur des cercles sont les seuils.Des cellules cachées
Le problème vient du fait que la cellule centrale de la figure 7.3 est une cellule cachée. Les données du problème ne fixent que les états des deux cellules d'entrée et de la cellule de sortie. Elles ne nous disent rien a priori sur l'état de la cellule centrale. Imaginer un algorithme permettant de faire varier le poids synaptique de cette cellule reviendrait à résoudre le problème de "l'attribution des récompenses" (en anglais credit assignment problem). L'activité d'une cellule cachée peut augmenter ou diminuer une fonction d'erreur entre le pattern de sortie calculé par le réseau et le pattern désiré: comment varier en conséquence les poids synaptiques d'une cellule sans savoir quel sera son état définitif dans le réseau "instruit", lors de la phase de reconnaissance? Rappelons que les algorithmes que nous avons développés jusqu'à présent supposent que tous les états des automates du réseau sont connus.
Au stade actuel de notre exposé, la situation est donc la suivante: nous entrevoyons bien que la classe des problèmes que nous pouvons résoudre s'étendra si nous utilisons des cellules cachées, mais nous ne disposons pas encore d'algorithme d'apprentissage.
Un peu d'histoire: la querelle du perceptron
Avant d'exposer une solution simple (maintenant que nous la connaissons!) à la question précédente, il peut être intéressant de noter que ce problème, énoncé formellement par M. Minsky et S. Papert en 1969, a pratiquement bloqué le développement de la recherche appliquée sur les réseaux d'automates pendant plus de dix ans. Résumons leur argumentation:
• Les perceptrons sont des séparateurs linéaires.
• Des fonctions de type OUex sont indispensables en reconnaissance des formes. (Un des exemples décrits concernait le problème de la reconnaissance du caractère connexe d'une figure qui nécessitait la réalisation d'une fonction OUex.)
• Or les perceptrons à une seule couche de cellules de décision ne peuvent apprendre des fonctions de ce type.
• Nous ne connaissons pas d'algorithmes d'apprentissage pour des réseaux à plusieurs couches. Nous n'en trouverons jamais; il faut donc arrêter la recherche sur ce sujet sans avenir.
Les perceptrons ne méritaient peut-être pas les folles espérances qu'avaient suscitées les premières recherches de F. Rosenblatt (1962), ni en tout cas les attaques inspirées par le livre de M. Minsky et S. Papert (1969). Il faut en fait se rappeler que la querelle du perceptron était au centre d'un débat entre d'une part les machines digitales et les machines analogiques (le perceptron était réalisé avec des rhéostats variables commandés par de gros moteurs lors de l'apprentissage), et d'autre part entre machines dédiées (comme le perceptron) et machines d'usage général. La technologie et les besoins, dès les années cinquante, conduisaient de toute façon au choix des machines digitales à usage général. Et c'est en fait grâce aux possibilités de simulation offertes par les machines digitales à usage général que le sujet s'est à nouveau développé depuis les années quatre-vingt.
7-2 LES RESEAUX EN COUCHES
7-2-1 Structure
Ces réseaux constituent aujourd'hui la réponse la mieux adaptée aux problèmes posés par les limites du perceptron et des modèles de Hopfield: ils permettent des classifications qui vont au-delà des classifications linéaires, et nous disposons d'algorithmes d'apprentissage leur permettant d'apprendre et de généraliser à partir d'exemples.
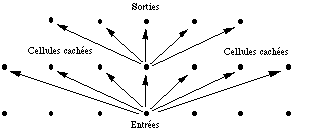
Figure 7.4
Le principe en est le suivant: il s'agit de systèmes dans lesquels le signal se propage, à chaque intervalle de temps, depuis une première couche d'entrée, à travers des couches intermédiaires successives, vers une couche de sortie.
Chaque cellule (sauf celles d'entrée) évalue une combinaison linéaire A de ses entrées prises dans la couche précédente, et compresse cette somme algébrique dans l'intervalle [-1,+1] (voir les exemples de fonctions de compression en 6.1.2). La somme algébrique comprend un terme de seuil - Q . La connectivité entre une cellule et la couche précédente est en général complète, du moins avant la phase d'apprentissage. Autrement dit, chaque cellule reçoit un signal de chacune des cellules de la couche précédente. A la différence des modèles de réseaux d'automates classiques, les unités sont donc analogiques et non pas logiques. Le signal de sortie d'une cellule i s'écrit:
![]()
![]()
où f est une fonction de compression, comme celles décrites au paragraphe 6.1.2, par exemple la fonction tangente hyperbolique:
![]()
![]()
dont la dérivée par rapport à A s'exprime simplement sous la forme:
y' = 1 - y2 (7.7)
L'architecture du réseau est susceptible de bien des variantes à l'intérieur de ce cadre: le nombre de cellules dans chacune des couches, pas plus que celui des couches intermédiaires, ne sont déterminés à l'avance. Ils peuvent varier dans une large gamme en fonction du problème à traiter.
Enfin, point capital, les poids synaptiques (et les seuils) sont appris en fonction des patterns présentés sur les cellules d'entrée et de leur classification présentée sur les cellules de sortie. On part de poids faibles, aléatoirement répartis, et l'on applique l'algorithme dit de rétro-propagation, décrit au paragraphe qui suit (7.2.2). On peut bien sûr imaginer des généralisations concernant la connectivité dans le réseau, mais l'algorithme de rétro-propagation ne s'applique qu'au cadre que nous venons de décrire.
7-2-2 La rétro-propagation
On recherche les poids synaptiques minimisant une fonction erreur C:
![]()
![]()
Les Y sont les sorties désirées, les S les sorties calculées par le réseau. L'indice i se rapporte aux cellules de la couche de sortie et l'indice s au pattern présenté. La somme s'étend donc à toutes les cellules de sortie et à tous les patterns présentés.
Nous allons appliquer une méthode de gradient: il faut donc calculer les composantes du gradient de l'erreur C dans l'espace des poids synaptiques, puis à chaque étape diminuer chaque poids synaptique d'une quantité proportionnelle à la dérivée partielle correspondante de la fonction erreur. De même que pour le perceptron, les seuils sont considérés comme des poids synaptiques transmettant l'état fixé à -1 d'une cellule j , à la cellule i considérée.
On commence par choisir une itération de type Widrow-Hoff: au lieu d'évaluer les gradients à partir de la fonction erreur sommée sur tous les patterns, on modifie les poids synaptiques à chaque présentation en ne tenant compte que de l'erreur sur le pattern présenté.
Une autre simplification dans l'écriture de l'algorithme consiste à introduire les variables intermédiaires Ai représentant les sommes pondérées des signaux de sortie des cellules j:
![]()
![]()
D'une manière générale la dérivée partielle de C par rapport à un poids synaptique fait intervenir un produit de deux termes:
![]()
![]()
Nous nous intéresserons donc aux dérivées par rapport aux variablesintermédiaires Ai, qu'il suffira ensuite de multiplier par les Sj pour obtenir les dérivées par rapport aux poids synaptiques correspondants.
La cascade des dérivées
Le calcul de l'état de chaque cellule de sortie fait intervenir les états des cellules intermédiaires par une imbrication d'expressions de même type:
![]()
![]()
![]()
![]()
![]()
![]()
On peut bien sûr calculer la dérivée de C par rapport à n'importe quel poids synaptique intermédiaire, en appliquant la formule de la dérivée des fonctions composées. La cascade ci-dessus permet de remarquer que l'imbrication des parenthèses, et par conséquent la complexité des calculs, croissent avec la profondeur des cellules. C'est le côté défavorable de cette expression. Elle présente aussi un côté favorable: si on calcule les dérivées en commençant par les cellules de sortie, et en poursuivant par couches successives vers l'entrée, la plupart des quantités nécessaires pour le calcul d'une dérivée d'une couche donnée ont déjà été calculées pour les autres couches situées plus près de la sortie. Il est donc logique d'utiliser une méthode itérative, dans laquelle le calcul des dérivées partielles se fait dans la direction inverse de la direction de propagation du signal: d'où le nom de rétro-propagation.
En définitive, l'algorithme d'apprentissage est le suivant:
Pour chaque présentation h d'un pattern s à l'entrée:
1. Phase de calcul des états:
Pour n variant de 2 à p, le nombre de couches (propagation dans le sens du signal):
On calcule l'état Si de chaque cellule i suivant:
![]()
![]()
2. Phase de calcul des gradients de l'erreur
Pour chaque cellule de sortie:
![]()
![]()
Pour n variant de p -1 à 1 (rétro-propagation):
Pour chaque cellule j de la couche n :
![]()
![]()
où l'indice i se rapporte aux cellules qui reçoivent le signal de la cellule j. (On peut paraphraser cette expression en disant que l'influence de la cellule j de la couche de profondeur n sur l'erreur C dépend de la somme des influences sur l'erreur des cellules i de la couche n +1, pondérées par les influences de j sur i (Tij), le tout modulé par la dérivée de la fonction sigmoïde au point Aj.)
3. Réajustement des poids synaptiques suivant l'algorithme du gradient:
![]()
![]()
pour la couche de sortie, et
![]()
![]()
pour les couches intermédiaires.
Architectures et performances des réseaux en couches
Nous avons dit que l'architecture du réseau dépendait du problème posé. Malheureusement, nous ne disposons pas aujourd'hui de méthodes permettant de déterminer l'architecture la mieux adaptée à un problème donné. Nous ne pouvons même pas prédire si une architecture est a priori capable de résoudre le problème posé. On peut se dire qu'une architecture comprenant un grand nombre de cellules réparties sur de multiples couches sera plus performante qu'une architecture simple, mais cette intuition n'est pas toujours utile car:
• les temps d'apprentissage croissent très vite avec la complexité du réseau;
• un réseau trop complexe n'est pas capable de généraliser à partir des exemples fournis. Plus précisement, l'ensemble de patterns à classer est souvent trop important pour que tous les patterns soient présentés lors de l'apprentissage. Seule une partie d'entre eux, l'ensemble d'apprentissage, est présentée. Les performances du réseau diffèrent donc dans la phase de reconnaissance entre l'ensemble d'apprentissage et les autres patterns. La possibilité de reconnaître ces derniers constitue la capacité de généralisation du réseau. Si le réseau est trop complexe, il se contente "d'apprendre par cœur" l'ensemble d'apprentissage, sans générer une représentation interne du problème qui lui permettrait de généraliser.
Autrement dit, nous disposons bien d'un algorithme, mais en face d'un problème il faut:
• choisir une architecture ni trop simple car elle limiterait la nature des corrélations que le réseau peut prendre en compte, ni trop complexe pour limiter les temps d'apprentissage et faciliter la généralisation;
• choisir le meilleur codage des patterns d'entrée et par conséquent la structure de la couche d'entrée. Le codage choisi est rarement le plus compact, ceci afin de faciliter l'apprentissage. On choisit de même le codage des classes d'équivalence pour la couche de sortie. Enfin, pour les couches intermédiaires, on commence par des essais d'apprentissage avec un nombre minimum de couches: une seule, voire aucune couche intermédiaire. On augmente ensuite progressivement ce nombre en fonction des résultats obtenus.
Le choix du nombre de présentations de chaque pattern dépend des variations successives des Tij observées au cours de l'apprentissage.
On teste dans une première phase les performances d'un réseau sur les exemples mêmes ayant servi à l'apprentissage. Puis on teste les capacités de généralisation par des patterns nouveaux qui n'ont jamais été présentés au réseau.
Le savoir-faire du praticien, comme bien souvent en informatique, conditionne donc la réussite d'une application.
7-2-3 Une application type: NETtalk
Les réseaux en couches, dont les possibilités ont d'abord été testées sur des problèmes simples, sont utilisés aujourd'hui en traitement du signal, en codage de l'information et en reconnaissance de patterns acoustiques ou d'images. Une application particulière, NETtalk, nous permettra de décrire quelques problèmes concrets, l'architecture retenue et les performances d'un système.
NETtalk transcrit les lettres d'un texte anglais en phonèmes, c'est-à-dire en éléments du langage (en français, la lettre c par exemple peut se prononcer suivant le phonème /s/ ou /k/). Les phonèmes codés de manière standard peuvent alors être envoyés sur un processeur spécialisé qui alimente un synthétiseur de sons. L'apprentissage se fait donc en présentant les lettres du texte sur la couche d'entrée, et les phonèmes correspondants, après le délai de propagation, sur la couche de sortie.
L'architecture du réseau est représentée sur la figure 7.5:
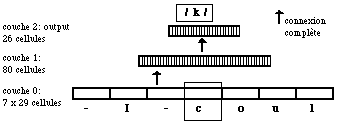
Figure 7.5
Un réseau à couches, NETtalk.Les entrées sont codées par place, ce qui signifie que l'on utilise autant de cellules que de caractères différents à coder. Une cellule correspond à un caractère; elle prend la valeur 1 si le caractère est présenté et -1 sinon. Ce codage est donc très peu économique. Pour coder les 29 caractères utilisés on emploie des ensembles de 29 cellules. La couche d'entrée est constituée de 7 ensembles de ce type. L'ensemble central reçoit comme entrée la lettre dont le phonème est à déterminer et les six ensembles voisins reçoivent les lettres voisines du texte: en effet, la difficulté du problème tient au fait que la correspondance lettre/phonème n'est pas bi-univoque mais qu'elle dépend du contexte. Trois lettres de part et d'autre de la lettre lue semblent suffisantes pour prendre en compte cet effet.
Une seule couche intermédiaire contient 80 cellules reliées à toutes les cellules d'entrée.
La couche de sortie correspond elle aussi à un codage par place des phonèmes possibles: elle comprend 26 cellules.
Performances
Le corpus présenté comprend un millier de mots. Le taux de reconnaissance atteint 95% après la présentation de 50 000 mots, ce qui donne un texte tout à fait intelligible, pour l'ensemble d'apprentissage. Les performances tombent à 78% lorsque les mots présentés ne font pas partie de l'ensemble d'apprentissage. Le temps nécessaire à l'apprentissage représente une nuit de fonctionnement d'un VAX 780 avec processeur flottant.
Rôle des cellules cachées
L'une des questions qui se posent toujours à propos des réseaux à couches est celle du rôle des cellules cachées. L'état de celles-ci est lié aux régularités qu'elles discernent dans les patterns présentés. Il s'agit en somme d'une véritable représentation interne des données. Dans le cas de NETalk, il semble, d'après T. Sejnowsky et C. Rosenberg, que certaines cellules cachées classifient les phonèmes suivant les règles de la phonétique classique. Autrement dit, certaines cellules cachées détectent les voyelles, d'autres les consonnes, ainsi que leur qualité de labiales, gutturales ou dentales.
Conclusions
La plupart des réseaux proposés pour le traitement du signal ont une architecture appartenant à l'une des deux catégories suivantes:
• Réseaux en couches, dans lesquels le signal se propage à chaque intervalle de temps d'une couche à l'autre. Dans ces modèles, les couches sont différentes et il n'y pas de boucles de rétroaction permettant au signal de revenir en arrière. Nous avons parlé ici du perceptron et des réseaux basés sur un apprentissage avec rétro-propagation, mais d'autres modèles ont aussi été proposés en particulier par K. Fukushima (le néo-cognitron) et B. Huberman (voir la bibliographie).
• Réseaux homogènes avec boucles de rétroaction, dans lesquels le signal est itéré jusqu'à ce qu'une configuration attractrice soit obtenue: c'est le cas des réseaux de Hopfield et des diverses variantes discutées au chapitre 6.
On peut bien entendu envisager de combiner les deux architectures pour obtenir des comportements plus riches, mais il faudrait alors envisager de nouveaux algorithmes d'apprentissage.
Références
Le premier classique sur le perceptron est le livre de F. Rosenblatt, Principles of Neurodynamics, Spartan Books, New York (1962). Le livre remarquablement clair de M. Minsky et S. Papert sur les limites du perceptron vient d'être réédité: M. Minsky, S. Papert: Perceptrons, Cambridge, MIT Press (1988).
Les réseaux en couches sont longuement décrits dans le livre collectif Parallel Distributed Processing, édité par J . Rumelhart, J. McClelland et le PDP Research Group, 2 vol., MIT Press (1986). Le troisième volume, édité en 1987, contient de nombreuses indications sur les algorithmes plus une disquette pour IBM PC et compatibles. Le chapitre "Automata Networks and Artificial Intelligence" du livre collectif Automata Networks in Computer Science, édité par F. Fogelman-Soulié, Y. Robert et M. Tchuente, Manchester University Press (1987), traite des formalismes linéaires et de la rétro-propagation en donnant quelques évaluations comparatives des différents algorithmes. Les problèmes de l'apprentissage et de la généralisation sont traités dans F. Fogelman-Soulié, "Network Learning", in Machine Learning, vol. 3, édité par Y. Kodratoff et R. Michalski, Morgan Kauffman, à paraître.
NETtalk est décrit dans T. Sejnowski, C. Rosenberg: "Parallel Networks that Learn to Pronounce English Text", Complex Systems, 1 (1987), 145-168.
Deux autres modèles de réseaux en couches sont décrits par K. Fukushima : "A Self-Organizing Multilayered Neural Network with a Function of Associative Memory: Feedback-Type Cognitron", Systems Computers Controls, 6 (1975), 15-22; et par B. Huberman et T. Hogg: "Adaptation and Self Repair in Parallel Computing Structures", Phys. Rev. Let., vol 52 (1984), 1048-1051.