Interacting Agents and Continuous Opinions Dynamics
Gérard Weisbuch
Guillaume Deffuant ,
Frederic Amblard
,
Frederic Amblard
and Jean Pierre Nadal
 Laboratoire
de Physique Statistique1
Laboratoire
de Physique Statistique1
de l'Ecole Normale Supérieure,
24 rue Lhomond, F-75231 Paris Cedex 5, France.
 Laboratoire
d'Ingénierie pour les Systèmes Complexes (LISC)
Laboratoire
d'Ingénierie pour les Systèmes Complexes (LISC)
Cemagref - Grpt de Clermont-Ferrand
24 Av. des Landais - BP50085
F-63172 Aubière Cedex (FRANCE)
email:weisbuch@lps.ens.fr
Abstract:
We present a model of opinion dynamics in which agents adjust continuous
opinions as a result of random binary encounters whenever their difference
in opinion is below a given threshold. High thresholds yield convergence
of opinions towards an average opinion, whereas low thresholds result in
several opinion clusters. The model is further generalised to network interactions,
threshold heterogeneity, adaptive thresholds and binary strings of opinions.
Introduction
Many models about opinion dynamics (Fölmer 1974, Arthur 1994, Orléan
1995, Latané and Nowak 1997, Weisbuch and
Boudjema 1999), are based on binary opinions which social actors update
as a result of social influence, often according to some version of a majority
rule. Binary opinion dynamics have been well studied, such as the herd
behaviour described by economists (Fölmer 1974, Arthur 1994, Orléan
1995). One expect that in most cases the attractor of the dynamics will
display uniformity of opinions, either 0 or 1, when interactions occur
across the whole population. Clusters of opposite opinions appear when
the dynamics occur on a social network with exchanges restricted to connected
agents. Clustering is reinforced when agent diversity, such as a disparity
in influence, is introduced, (Latané and Nowak 1997, Weisbuch and
Boudjema 1999).
One issue of interest concerns the importance of the binary assumption:
what would happen if opinion were a continuous variable such as the worthiness
of a choice (a utility in economics), or some belief about the adjustment
of a control parameter?
The rationale for binary versus continuous opinions might be related
to the kind of information used by agents to validate their own choice:
-
the actual choice of the other agents, a situation common in economic choice
of brands: "do as the others do";
-
the actual opinion of the other agents, about the "value" of a choice:
"establish one's opinion according to what the others think or at least
according to what they say".
On the empirical side, there exist well documented studies about social
norms concerning sharing between partners. Henrich et al. (2001)
compared through experiments shares accepted in the ultimatum game and
showed that people agree upon what a "fair" share should be, which can
of course vary across different cultures. Young and Burke (2000) report
empirical data about crop sharing contracts, whereby a landlord leases
his farm to a tenant laborer in return for a fixed share of the crops.
In Illinois as well as in India, crop sharing distributions are strongly
peaked upon "simple values" such as 1/2-1/2 or 1/3-2/3. The clustering
of opinions about "fair shares" is the kind of stylised fact that our model
tries to reproduce. More generally, we expect such opinion dynamics to
occur in situation where agents have to make important choices and care
to collect many opinions before taking any decisions: adopting a technological
change might often be the case. The present paper was motivated by changes
towards environmental-friendly practices in agriculture under the influence
of the new Common Agricultural Policy in Europe.
Modeling of continuous opinions dynamics was earlier started by applied
mathematicians and focused on the conditions under which a panel of experts
would reach a consensus, (Stone 1961, Chatterjee and Seneta 1977, Cohen
et al.1986, Laslier 1989, Krause 2000, Hegselmann and Krause 2002,
further referred to as the "consensus" literature).
The purpose of this paper is to present results concerning continuous
opinion dynamics subject to the constraint that convergent opinion adjustment
only proceeds when opinion difference is below a given threshold. The rationale
for the threshold condition is that agents only interact when their opinions
are already close enough; otherwise they do not even bother to discuss.
The reason for refusing discussion might be for instance lack of understanding,
conflicting interest, or social pressure. The threshold would then correspond
to some openness character. Another interpretation is that the threshold
corresponds to uncertainty: the agents have some initial views with some
degree of uncertainty and would not care about other views outside their
uncertainty range.
Many variants of the basic idea can be proposed and the paper is organised
as follows:
-
We first expose the simple case of complete mixing among agents under a
unique and constant threshold condition.
-
We then check the genericity of the results obtained for the simplest model
to other cases such as localised interactions, distribution of thresholds,
varying thresholds and binary strings of opinions.
A previous paper (Deffuant et al.2000) reported more complete results
on mixing across a social network and on binary strings of opinions.
The basic case: Complete Mixing
and one fixed threshold
Let us consider a population of  agents
agents 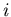 with continuous opinion
with continuous opinion 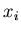 .
We start from an initial distribution of opinions, most often taken uniform
on [0,1] in the computer simulations. At each time step any two randomly
chosen agents meet: they re-adjust their opinion when their difference
in opinion is smaller in magnitude than a threshold
.
We start from an initial distribution of opinions, most often taken uniform
on [0,1] in the computer simulations. At each time step any two randomly
chosen agents meet: they re-adjust their opinion when their difference
in opinion is smaller in magnitude than a threshold 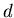 .
Suppose that the two agents have opinion
.
Suppose that the two agents have opinion  and
and 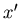 .
.
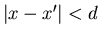 opinions are adjusted according to:
opinions are adjusted according to:
where  is the convergence parameter whose values may range from 0 to 0.5.
is the convergence parameter whose values may range from 0 to 0.5.
In the basic model, the threshold 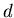 is taken as constant in time and across the whole population. Note that
we here apply a complete mixing hypothesis plus a random serial iteration
mode2.
is taken as constant in time and across the whole population. Note that
we here apply a complete mixing hypothesis plus a random serial iteration
mode2.
The evolution of opinions may be mathematically predicted in the limiting
case of small values of 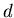 (Neau 2000)3.
Time variations of opinions' density
(Neau 2000)3.
Time variations of opinions' density 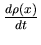 obey the following dynamics:
obey the following dynamics:

This implies that starting from an initial distribution of opinions
in the population, any local higher opinion density is amplified. Peaks
of opinions increase and valleys are depleted until very narrow peaks remain
among a desert of intermediate opinions.
For finite thresholds, computer simulations show that the distribution
of opinions evolves at large times towards clusters of homogeneous opinions.
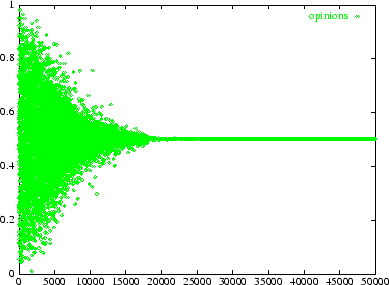 |
Figure: Time chart of opinions ( ).
One time unit corresponds to sampling a pair of agents.
).
One time unit corresponds to sampling a pair of agents.
-
For large threshold values (
 )
only one cluster is observed at the average initial opinion. Figure 1 represents
the time evolution of opinions starting from a uniform distribution of
opinions.
)
only one cluster is observed at the average initial opinion. Figure 1 represents
the time evolution of opinions starting from a uniform distribution of
opinions.
-
For lower threshold values, several clusters can be observed (see figure
2). Consensus is then NOT achieved when thresholds are low enough.
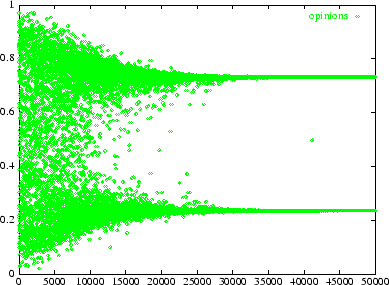 |
Figure 2: Time chart of opinions for a lower
threshold  (
( )
.
)
.
Obtaining clusters of different opinions does not surprise an observer
of human societies, but this result was not a priori obvious since we started
from an initial configuration where transitivity of opinion propagation
was possible through the entire population: any two agents however different
in opinions could have been related through a chain of agents with closer
opinions. The dynamics that we describe ended up in gathering opinions
in clusters on the one hand, but also in separating the clusters in such
a way that agents in different clusters don't exchange anymore.
The number of clusters varies as the integer part of 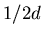 :
this is to be further referred to as the "1/2d rule" (see figure 34).
:
this is to be further referred to as the "1/2d rule" (see figure 34).
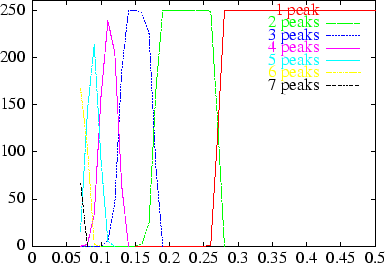 |
Figure 3: Statistics of the number of opinion
clusters as a function of 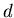 on the x axis for 250 samples (
on the x axis for 250 samples ( ).
).
Social Networks
The literature on social influence and social choice also considers the
case when interactions occur along social connections between agents (Fölmer
1974) rather than randomly across the whole population. Apart from the
similarity condition, we now add to our model a condition on proximity,
i.e. agents only interact if they are directly connected through a pre-existing
social relation. Although one might certainly consider the possibility
that opinions on certain un-significant subjects could be influenced by
complete strangers, we expect important decisions to be influenced by advice
taken either from professionals (doctors, for instance) or from socially
connected persons (e.g. through family, business, or clubs). Facing the
difficulty of inventing a credible instance of a social network as in the
literature on social binary choice, we here adopted the standard simplification
and carried out our simulations on square lattices: square lattices are
simple, allow easy visualisation of opinion configurations and contain
many short loops, a property that they share with real social networks.
We then started from a 2 dimensional network of connected agents on
a square grid. Any agent can only interact with his four connected neighbours
(N, S, E and W). We used the same initial random sampling of opinions from
0 to 1 and the same basic interaction process between agents as in the
previous sections. At each time step a pair is randomly selected among
connected agents and opinions are updated according to equations
1 and 2 provided of course that their distance is less than 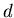 .
.
The results are not very different from those observed with non-local
opinion mixing as described in the previous section, at least for the larger
values of 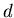 (
( ,
all results displayed in this section are equilibrium results at large
times). As seen in figure 4, the lattice is filled with a large majority
of agents who have reached consensus around
,
all results displayed in this section are equilibrium results at large
times). As seen in figure 4, the lattice is filled with a large majority
of agents who have reached consensus around 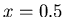 while a few isolated agents have ``extremists'' opinions closer to 0 or
1. The importance of extremists is the most noticeable difference with
the full mixing case described in the previous section.
while a few isolated agents have ``extremists'' opinions closer to 0 or
1. The importance of extremists is the most noticeable difference with
the full mixing case described in the previous section.
 |
Figure: Display of final opinions of agents
connected on a square lattice of size 29x29 ( after 100 000 iterations) . Opinions between 0 and 1 are coded by gray
level (0 is black and 1 is white). Note the percolation of the large cluster
of homogeneous opinion and the presence of isolated ``extremists''.
after 100 000 iterations) . Opinions between 0 and 1 are coded by gray
level (0 is black and 1 is white). Note the percolation of the large cluster
of homogeneous opinion and the presence of isolated ``extremists''.
Interesting differences are noticeable for the smaller values of  as observed in figure 5.
as observed in figure 5.
 |
Figure: Display of final opinions of agents
connected on a square lattice of size 29x29 ( after 100 000 iterations) . Color code: purple 0.14, light blue 0.42, red
0.81 to 0.87. Note the presence of smaller clusters with similar but not
identical opinions.
after 100 000 iterations) . Color code: purple 0.14, light blue 0.42, red
0.81 to 0.87. Note the presence of smaller clusters with similar but not
identical opinions.
For connectivity 4 on a square lattice, only cluster percolates (Stauffer
and Aharony 1994) across the lattice. All agents of the percolating cluster
share the same opinion as observed on figure 4. But for  several opinion clusters are observed and none percolates across the lattice.
Similar opinions, but not identical, are shared across several clusters.
The differences of opinions between groups of clusters relate to
several opinion clusters are observed and none percolates across the lattice.
Similar opinions, but not identical, are shared across several clusters.
The differences of opinions between groups of clusters relate to 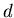 ,
but the actual values inside a group of clusters fluctuate from cluster
to cluster because homogenisation occurred independently among the different
clusters: the resulting opinion depends on fluctuations of initial opinions
and histories from one cluster to the other. The same increase in fluctuations
compared to the full mixing case is observed from sample to sample with
the same parameter values.
,
but the actual values inside a group of clusters fluctuate from cluster
to cluster because homogenisation occurred independently among the different
clusters: the resulting opinion depends on fluctuations of initial opinions
and histories from one cluster to the other. The same increase in fluctuations
compared to the full mixing case is observed from sample to sample with
the same parameter values.
The qualitative results obtained with 2D lattices should be observed
with any connectivity, either periodic, random, or small world.
The above results where obtained when all agents have the same invariant
threshold. The purpose of the following sections is to check the general
character of our conclusions:
-
when one introduces a distribution of thresholds in the population;
-
when the thresholds themselves obey some dynamics.
Heterogeneous constant threshold
Supposing that all agents use the same threshold to decide whether to take
into account the views of other agents is a simplifying assumption. When
heterogeneity of thresholds is introduced, some new features appear. To
simplify the matter, let us exemplify the issue in the case of a bimodal
distribution of thresholds, for instance 8 agents with a large threshold
of 0.4 and 192 with a narrow threshold of 0.2 as in figure 6.
 |
Figure 6: Time chart of opinions (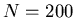 ).
Red '+' represent narrow minded opinions (192 agents with threshold 0.2),
green 'x' represent open minded opinions (8 agents with threshold 0.4).
).
Red '+' represent narrow minded opinions (192 agents with threshold 0.2),
green 'x' represent open minded opinions (8 agents with threshold 0.4).
One observes that in the long run convergence of opinions into one single
cluster is achieved due to the presence of the few "open minded" agents
(the single cluster convergence time is 12000, corresponding to 60 iterations
per agent on average, for the parameters of figure 6). But in the short
run, a metastable situation with two large opinion clusters close to opinions
0.35 and 0.75 is observed due to narrow minded agents, with open minded
agents opinions fluctuating around 0.5 due to interactions with narrow
minded agents belonging to either high or low opinion cluster. Because
of the few exchanges with the high 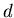 agents, low
agents, low 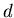 agents opinions slowly shift towards the average until the difference in
opinions between the two clusters falls below the low threshold: at this
point the two clusters collapse.
agents opinions slowly shift towards the average until the difference in
opinions between the two clusters falls below the low threshold: at this
point the two clusters collapse.
This behaviour is generic for any mixtures of thresholds. At any time
scale, the number of clusters obeys a "generalized 1/2d rule":
-
on the long run clustering depends on the higher threshold;
-
on the short run clustering depends on the lower threshold;
-
the transition time between the two dynamics is proportional to the total
number of agents and to the ratio of narrow minded to open minded agents.
In some sense, the existence of a few "open minded" agents seems sufficient
to ensure consensus after a large enough time for convergence. The next
section restrict the validity of this prediction when threshold dynamics
are themselves taken into account.
Threshold Dynamics
Let us interprete the basic threshold rule in terms of agent's uncertainty:
agents take into account others' opinion on the occasion of interaction
because they are not certain about the worthiness of a choice. They engage
in interaction only with those agents which opinion does not differ too
much from their own opinion in proportion of their own uncertainty. If
we interprete the threshold for exchange as the agent uncertainty, we might
suppose with some rationale that his subjective uncertainty decreases with
the number of opinion exchanges.
Taking opinions from other agents can be interpreted, at least by the
agent himself, as sampling a distribution of opinions. As a result of this
sampling, agents should update their new opinion by averaging over their
previous opinion and the sampled external opinion and update the variance
of the opinion distribution accordingly.
Within this interpretation, a "rational procedure" (in the sense of
Herbert Simon) for the agent is to simultaneously update his opinion and
his subjective uncertainty. Let us write opinion updating as weighting
one's previous opinion 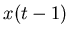 by
by  and the other agent's opinion
and the other agent's opinion 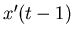 by
by  ,
with
,
with 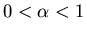 .
. can be re-written
can be re-written 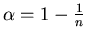 where
where 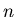 expresses a characteristic number of opinions taken into account in the
averaging process.
expresses a characteristic number of opinions taken into account in the
averaging process. is then a relative weight of the agent previous opinion as compared to
the newly sampled opinion weighted
is then a relative weight of the agent previous opinion as compared to
the newly sampled opinion weighted 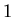 .
Within this interpretation, updates of both opinion
.
Within this interpretation, updates of both opinion  and variance
and variance  should be written:
should be written:
The second equation simply represents the change in variance when
the number of samples increases from  at time
at time 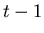 to
to 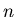 at time
at time 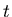 .
It is directly obtained from the definition of variance as a weighted sum
of squared deviations.
.
It is directly obtained from the definition of variance as a weighted sum
of squared deviations.
As previously, updating occurs when the difference in opinion is lesser
than a threshold, but this threshold is now related to the variance of
the distribution of opinions sampled by the agent. A simple choice is to
relate the threshold to the standard deviation 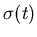 according to:
according to:
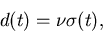 |
(5) |
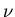 is a constant parameter often taken equal to 1 in the simulations.
is a constant parameter often taken equal to 1 in the simulations.
When an agent equally values collected opinions independently of how
old they are, he should also update  connected to
connected to  the number of previously collected opinions:
the number of previously collected opinions:
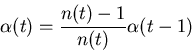 |
(6) |
Another possible updating choice is to maintain  constant which corresponds to taking a moving average on opinions and giving
more importance to the
constant which corresponds to taking a moving average on opinions and giving
more importance to the 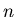 later collected opinions. Such a "bounded" memory would make sense in the
case when the agent believes that there exists some slow shift in the distribution
of opinions, whatever its cause, and that older opinions should be discarded.
later collected opinions. Such a "bounded" memory would make sense in the
case when the agent believes that there exists some slow shift in the distribution
of opinions, whatever its cause, and that older opinions should be discarded.
Both algorithms were tried in the simulations and give qualitatively
similar results in terms of the number of attractors, provided that one
starts from an initial number of supposed trials 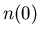 corresponding to the same
corresponding to the same  .
.
Scaling
Constant 
In the case of constant  ,
a simplified computation valid in the limit of small
,
a simplified computation valid in the limit of small 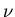 predicts an exponential decay of thresholds. Neglecting the second term
in the dynamics of variance 5
:
predicts an exponential decay of thresholds. Neglecting the second term
in the dynamics of variance 5
:
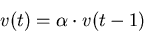 |
(7) |
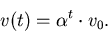 |
(8) |
 as
as  and approximating it as exp
and approximating it as exp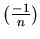 for large
for large 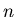 ,
we
see that the variance decays exponentially with a characteristic time of
,
we
see that the variance decays exponentially with a characteristic time of 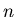 and that the thresholds vary as:
and that the thresholds vary as:
![\begin{displaymath}d(t) \simeq d_0 \cdot exp [- \frac{t}{2n}]\end{displaymath}](img74.gif) |
(9) |
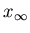 (corresponding to the attractor) can be made by replacing
(corresponding to the attractor) can be made by replacing 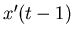 by
by 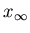 in equation (3) describing the dynamics of
in equation (3) describing the dynamics of 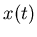 .
After subtracting
.
After subtracting 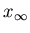 to both members, the deviation of opinions from their attractor can be
written as:
to both members, the deviation of opinions from their attractor can be
written as:
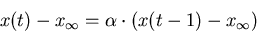 |
(10) |
Varying 
Equivalent computations were also made for the case when  varies as
varies as  .
For instance, the dynamics of variance is described by the following set
of equations:
.
For instance, the dynamics of variance is described by the following set
of equations:
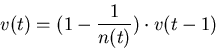 |
(11) |
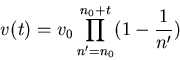 |
(12) |
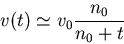 |
(13) |
The equivalent computation for the evolution of opinion deviation from
the attractor also gives an hyperbolic decay:
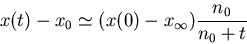 |
(14) |
-
The variable
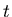 appearing in the expressions is NOT time, but the number of ACTUAL updates
of the agent opinions. The time scaling laws, exponential or hyperbolic
are the same for both variance and distance to the attractor. When going
from time to number of updates, one should take into account the frequency
of sampling one agent and the probability of actually updating the agent
which is proportional to the inverse number of attractors. With this caveat,
the simulations results are in accordance with the above predictions.
appearing in the expressions is NOT time, but the number of ACTUAL updates
of the agent opinions. The time scaling laws, exponential or hyperbolic
are the same for both variance and distance to the attractor. When going
from time to number of updates, one should take into account the frequency
of sampling one agent and the probability of actually updating the agent
which is proportional to the inverse number of attractors. With this caveat,
the simulations results are in accordance with the above predictions.
-
The scaling laws are different for constant and varying
 ,
with faster convergence (exponential) when
,
with faster convergence (exponential) when  is kept constant. But one should note that in both cases opinions dynamics
follow the same scaling rules as thresholds dynamics: phenomena such as
clustering should then be similar. The same dynamics of opinions and thresholds
are to be observed in both conditions provided that the horizontal axis
used to plot opinions for varying
is kept constant. But one should note that in both cases opinions dynamics
follow the same scaling rules as thresholds dynamics: phenomena such as
clustering should then be similar. The same dynamics of opinions and thresholds
are to be observed in both conditions provided that the horizontal axis
used to plot opinions for varying  is warped to an exponential for constant
is warped to an exponential for constant  .
.
Simulation Results
When comparing to constant threshold dynamics, decreasing thresholds results
in a larger variety of final opinions. For initial thresholds values which
would have ended in opinion consensus, one observes a number of final clusters
which decreases with  (and thus with
(and thus with 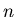 ).
Smaller values of
).
Smaller values of  correspond to a fast decrease of the thresholds, which prevents the aggregation
of all opinions into large clusters.
correspond to a fast decrease of the thresholds, which prevents the aggregation
of all opinions into large clusters.
Observing the chart of final opinions versus initial opinions on figure
7, one sees that most opinions converge towards two clusters (at 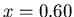 and
and 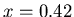 )
which are closer than those one could obtain with constant thresholds (typically
around
)
which are closer than those one could obtain with constant thresholds (typically
around 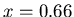 and
and  ):
initial convergence gathered opinions which would had aggregate at the
initial threshold values, but which later segregate due to the decrease
in thresholds. Many outliers are apparent on the plot.
):
initial convergence gathered opinions which would had aggregate at the
initial threshold values, but which later segregate due to the decrease
in thresholds. Many outliers are apparent on the plot.
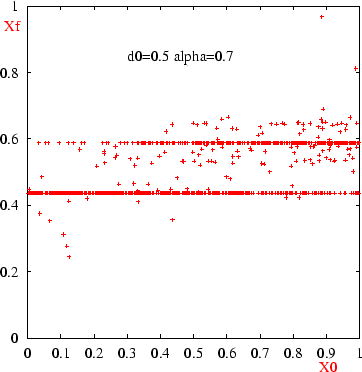 |
Figure: Each point on this chart represents
the final opinion of one agent versus its initial opinion (for constant 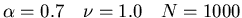 ,
initial threshold 0.5).
,
initial threshold 0.5).
Large  and
and 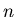
Large values of  ,
close to one, e.g.
,
close to one, e.g. 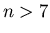 ,
correspond to averaging on many interactions. The interpretation of large
,
correspond to averaging on many interactions. The interpretation of large  and
and 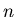 is that the agent has more confidence in his own opinion than in the opinion
of the other agent with whom he is interacting, in proportion with
is that the agent has more confidence in his own opinion than in the opinion
of the other agent with whom he is interacting, in proportion with  .
.
For constant values of  ,
the observed dynamics is not very different from what we obtained with
constant thresholds.
,
the observed dynamics is not very different from what we obtained with
constant thresholds.
The exponential decay of thresholds predicted by equation 9 is verified
on figure 8 plotted for the same parameters values. The observed decay
constant on figure 8 is 1.7, slightly less than 2, the theoretical prediction
based on equation 9 which neglects the possible increase of variance due
to other opinions.
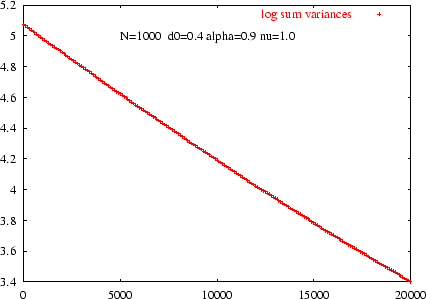 |
Figure: Exponential decay of summed variances
(for constant  ,
initial threshold 0.4).
,
initial threshold 0.4).
For  varying according to equation 13, the variance dynamics is hyperbolic as
observed on the log-log plot of figure 9. The observed slope on figure
9 is not far from the predicted value, -1.0.
varying according to equation 13, the variance dynamics is hyperbolic as
observed on the log-log plot of figure 9. The observed slope on figure
9 is not far from the predicted value, -1.0.
In both cases the scaling of variance and thresholds is verified on
more than one decade, but deviations are observed:
-
for varying
 ,
clustering is slow and deviations are observed at small times when the
segregation of clusters is not yet achieved because the probability of
updating a random pair is not yet constant;
,
clustering is slow and deviations are observed at small times when the
segregation of clusters is not yet achieved because the probability of
updating a random pair is not yet constant;
-
for constant
 ,
deviations are observed at large times due to the existence of outliers
which maintain a larger variance (see the next section).
,
deviations are observed at large times due to the existence of outliers
which maintain a larger variance (see the next section).
 |
Figure 9: Power-law decay of summed variances
for varying  ( log-log plot, initial
( log-log plot, initial  ).
).
Small  and
and 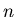
 |
Figure 10: Variation of the dispersion index 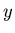 with
with 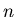 ,
the initial "subjective" number of collected opinions (
,
the initial "subjective" number of collected opinions ( 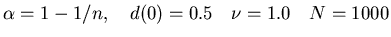 ).
The initial threshold value of 0.5 if kept constant would yield consensus
with only one cluster.
).
The initial threshold value of 0.5 if kept constant would yield consensus
with only one cluster.
A more complicated dynamics is observed for lower values of 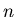 and
and  .
Apart from the expected main clusters, one also observes large and small
clusters plus isolated individuals (outliers).
.
Apart from the expected main clusters, one also observes large and small
clusters plus isolated individuals (outliers).
For 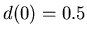 (which would yield consensus with only one cluster if kept constant) and
(which would yield consensus with only one cluster if kept constant) and 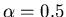 (corresponding to
(corresponding to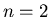 ,
i.e. agents giving equal weight to their own opinion and to the external
opinion), more than ten clusters unequal in size are observed plus isolated
outliers. One way to characterise the dispersion of opinions with varying
,
i.e. agents giving equal weight to their own opinion and to the external
opinion), more than ten clusters unequal in size are observed plus isolated
outliers. One way to characterise the dispersion of opinions with varying  is to compute
is to compute 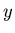 the relative value of the squared cluster sizes with respect to the squared
number of opinions.
the relative value of the squared cluster sizes with respect to the squared
number of opinions.
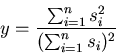 |
(15) |
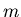 clusters of equal size, one would have
clusters of equal size, one would have  .
The smaller
.
The smaller 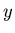 ,
the more important is the dispersion in opinions. Figure 10 shows the increase
of the dispersion index
,
the more important is the dispersion in opinions. Figure 10 shows the increase
of the dispersion index 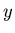 with
with 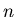 (
( is the initial "subjective" weight of agent's own opinion).
is the initial "subjective" weight of agent's own opinion).
As previously noticed on figure 7, some outliers do not aggregate in
the large clusters. The origin of these isolated agents is due to randomness
of:
-
sampling the individual agents at various times;
-
sampling the pairs, i.e. which pair of agent is sampled for possible interaction.
 |
Figure: Time chart of opinions and thresholds
(for constant 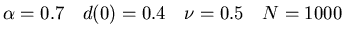 ).
Red '+' represent opinions and green 'x' represent thresholds.
).
Red '+' represent opinions and green 'x' represent thresholds.
The time pattern of thresholds appearing as green bands on figure 11 give
us some insight on these effects. One band corresponds to a given number
of opinion exchanges experienced by the agents: the upper band corresponds
to the variance after one exchange, the second upper to two exchanges and
so on. The lower bound of a band corresponds to the result of interactions
between very close opinions when the second term in equation 4 is negligible.
The vertical width of a band is due to this second term, which relative
importance to the first can be estimated from the figure: it is roughly
10 perc. (for 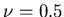 ).
The horizontal width of a band corresponds to the fact that different agents
are experiencing the same number of updating at different times: rough
evaluations made on figure 11 show that most agents have their first exchange
between time 0 and 4000, and their fifth exchange between 1000 and 12 000.
).
The horizontal width of a band corresponds to the fact that different agents
are experiencing the same number of updating at different times: rough
evaluations made on figure 11 show that most agents have their first exchange
between time 0 and 4000, and their fifth exchange between 1000 and 12 000.
When the decrease of threshold and the clustering of opinions is fast,
those agents which are not sampled early enough and/or not paired with
close enough agents can be left over from the clustering process. When
they are sampled later, they might be too far from the other agents to
get involved into opinion adjustment. The effect gets important when convergence
is fast, i.e. when 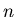 and
and  are small.
are small.
Let us note that these agents in the minority have larger uncertainty
and are more "open to discussion" than those in the mainstream, in contrast
with the common view that eccentrics are opinionated! For 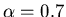 ,
,  ,
, 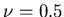 and
and 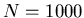 ,
the parameters of figure 11, we found that mainstream agents in the two
attractors account for 43 and 42 perc. of the population while 15 perc.
are in the minority peaks.
,
the parameters of figure 11, we found that mainstream agents in the two
attractors account for 43 and 42 perc. of the population while 15 perc.
are in the minority peaks.
The results of the dynamics are even more dispersed for lower values
of  .
In this regime, corresponding to "insecure agents" who don't value their
own opinion more than those of other agents, we observe more clusters which
importance and localisation depend on the random sampling of interacting
agents and are thus harder to predict than in the other regime with a small
number of big clusters. Using a physical metaphor, clustering in this regime
resembles quenching to a frozen configuration, thus maintaining many "defects"
(e.g. here the outliers), while the opposite regime it resembles annealing
(with suppression of defects).
.
In this regime, corresponding to "insecure agents" who don't value their
own opinion more than those of other agents, we observe more clusters which
importance and localisation depend on the random sampling of interacting
agents and are thus harder to predict than in the other regime with a small
number of big clusters. Using a physical metaphor, clustering in this regime
resembles quenching to a frozen configuration, thus maintaining many "defects"
(e.g. here the outliers), while the opposite regime it resembles annealing
(with suppression of defects).
In fact, one way to evaluate the influence of the two effects, randomness
of the time at which agents are sampled from randomness of pairing, is
to compare the standard random updating iteration that we have used to
parallel updating: in a parallel updating, a random pair matching of all
agents is first realised and all pairs are then updated simultaneously.
Parallel updating then suppresses randomness of updating time: only randomness
of pairing remains.
We found by comparing the two algorithms, random and parallel, for the
same set of parameters, that parallel updating only slightly reduces the
number of outliers. We can then conclude that most of the observed disorder
results from the randomness of pairing.
Distribution and Dynamics of
thresholds
Finally, an obvious set of simulations to perform is to have a distribution
of thresholds and to let these thresholds evolve according to one of the
two rules,  constant or decreasing, according to equation 5.
constant or decreasing, according to equation 5.
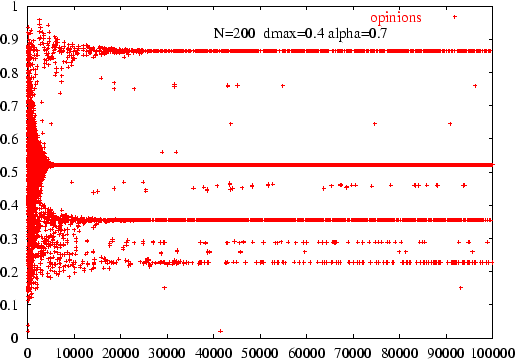 |
Figure: Time chart of opinions for a distribution
of varying thresholds (constant 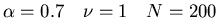 ).
The initial thresholds are uniformly distributed on
).
The initial thresholds are uniformly distributed on ![$[0,0.4]$](img17.gif) .
.
We used a uniform distribution of thresholds on ![$[0, d_{max}]$](img109.gif) and observed, not surprisingly since some thresholds are close to zero
even at initial times, that clusters and outliers are in larger number
than for single initial thresholds. Figure 12 displays the time evolution
of opinions for a constant value of
and observed, not surprisingly since some thresholds are close to zero
even at initial times, that clusters and outliers are in larger number
than for single initial thresholds. Figure 12 displays the time evolution
of opinions for a constant value of 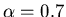 ,
, 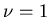 and
and 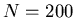 .
The initial thresholds were uniformly distributed on
.
The initial thresholds were uniformly distributed on ![$[0,0.63]$](img111.gif) .
Clusters correspond to agents with larger thresholds, outliers to thresholds
close to 0.
.
Clusters correspond to agents with larger thresholds, outliers to thresholds
close to 0.
Convergence times differ according to the size of the clusters: agents
in large clusters have more occasions to update their opinion in proportion
to the number of agents in the same cluster. Small clusters then need longer
times to get stabilised.
These results generalise and summarise our previous findings in sections
4, 5.1 and 5.2.
Vector opinions
The model
Another subject for investigation is vectors of opinions. Usually people
have opinions on different subjects, which can be represented by vectors
of opinions. In accordance with our previous hypotheses, we suppose that
one agent interacts concerning different subjects with another agent according
to some distance with the other agent's vector of opinions. In order to
simplify the model, we revert to binary opinions. An agent is characterised
by a vector of 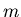 binary opinions about the complete set of
binary opinions about the complete set of 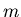 subjects, shared by all agents. We use the notion of Hamming distance between
binary opinion vectors (the Hamming distance between two binary opinion
vectors is the number of different bits between the two vectors). Here,
we only treat the case of complete mixing; any pair of agents might interact
and adjust opinions according to how many opinions they share.6
The adjustment process occurs when agents agree on at least
subjects, shared by all agents. We use the notion of Hamming distance between
binary opinion vectors (the Hamming distance between two binary opinion
vectors is the number of different bits between the two vectors). Here,
we only treat the case of complete mixing; any pair of agents might interact
and adjust opinions according to how many opinions they share.6
The adjustment process occurs when agents agree on at least  subjects (i. e. they disagree on
subjects (i. e. they disagree on 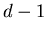 or fewer subjects). The rules for adjustment are as follows: when opinions
on a subject differ, one agent (randomly selected from the pair) is convinced
by the other agent with probability
or fewer subjects). The rules for adjustment are as follows: when opinions
on a subject differ, one agent (randomly selected from the pair) is convinced
by the other agent with probability  .
Obviously this model has connections with population genetics in the presence
of sexual recombination when reproduction only occurs if genome distance
is smaller than a given threshold. Such a dynamics results in the emergence
of species (see Higgs and Derrida 1991). We are again interested in the
clustering of opinion vectors. In fact clusters of opinions here play the
same role as biological species in evolution.
.
Obviously this model has connections with population genetics in the presence
of sexual recombination when reproduction only occurs if genome distance
is smaller than a given threshold. Such a dynamics results in the emergence
of species (see Higgs and Derrida 1991). We are again interested in the
clustering of opinion vectors. In fact clusters of opinions here play the
same role as biological species in evolution.
Results
We observed once again that  and
and  only modify convergence times towards equilibrium; the most influential
factors are threshold
only modify convergence times towards equilibrium; the most influential
factors are threshold 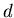 and
and 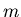 the number of subjects under discussion. Most simulations were done for
the number of subjects under discussion. Most simulations were done for  .
For
.
For 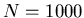 ,
convergence times are of the order of 10 million pair iterations. For
,
convergence times are of the order of 10 million pair iterations. For  :
:
-
When
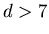 ,
the radius of the hypercube, convergence towards a single opinion occurs
(the radius of the hypercube is half its diameter which is equal to 13,
the maximum distance in the hypercube).
,
the radius of the hypercube, convergence towards a single opinion occurs
(the radius of the hypercube is half its diameter which is equal to 13,
the maximum distance in the hypercube).
-
Between
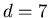 and
and 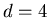 a similar convergence is observed for more than 99.5 per cent of the agents
with the exception of a few clustered or isolated opinions distant from
the main peak by roughly 7.
a similar convergence is observed for more than 99.5 per cent of the agents
with the exception of a few clustered or isolated opinions distant from
the main peak by roughly 7.
-
For
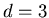 ,
one observes from 2 to 7 significant peaks (with a population larger than
1 per cent) plus some isolated opinions.
,
one observes from 2 to 7 significant peaks (with a population larger than
1 per cent) plus some isolated opinions.
-
For
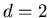 a large number (around 500) of small clusters is observed (The number of
opinions is still smaller than the maximum number of opinions within a
distance of 2).
a large number (around 500) of small clusters is observed (The number of
opinions is still smaller than the maximum number of opinions within a
distance of 2).
The same kind of results are obtained with larger values of 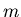 :
two regimes, uniformity of opinions for larger
:
two regimes, uniformity of opinions for larger 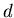 values and extreme diversity for smaller
values and extreme diversity for smaller 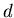 values, are separated by one
values, are separated by one 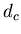 value for which a small number of clusters is observed (e.g for
value for which a small number of clusters is observed (e.g for  ,
,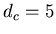 .
. 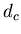 seems to scale in proportion with
seems to scale in proportion with 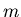 ).
).
Figure 13 represents these populations of the different clusters at
equilibrium (iteration time was 12 000 000) in a log-log plot according
to their rank-order of size. No scaling law is obvious from these plots,
but we observe the strong qualitative difference in decay rates for various
thresholds 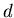 .
.
 |
Figure 13: Log-log plot of average populations
of clusters of opinions arranged by decreasing order for 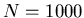 agents (
agents ( ).
).
Conclusion
The main lesson from this set of simulations is that opinion exchanges
restricted by a proximity threshold result into clustering of opinions.
The 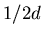 rule predicts the outcome of the dynamics in the simplest cases, but it
also provides some qualitative insight for the case of threshold dynamics.
rule predicts the outcome of the dynamics in the simplest cases, but it
also provides some qualitative insight for the case of threshold dynamics.
Continuous opinions and binary strings share some similarity: clustering
with a number of clusters decreasing with 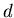 .
But continuous opinions display a regular decrease of cluster number with
.
But continuous opinions display a regular decrease of cluster number with 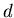 while binary strings display a phase transition from consensus to a large
multiplicity of clusters.
while binary strings display a phase transition from consensus to a large
multiplicity of clusters.
When one introduces dynamics on thresholds on the basis that agents
interprete opinion exchange as sampling a distribution of opinions:
-
The amplitude of
 and
and 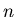 determine clustering properties.
determine clustering properties.
-
For large
 and
and 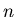 ,
when agents trust their own opinion more that the opinion of any other
agent, updating is smooth resulting in large clusters (annealing).
,
when agents trust their own opinion more that the opinion of any other
agent, updating is smooth resulting in large clusters (annealing).
-
For small
 and
and 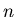 ,
with relatively "insecure" agents, updating is irregular resulting in more
clusters and outliers (quenching).
,
with relatively "insecure" agents, updating is irregular resulting in more
clusters and outliers (quenching).
-
Maintaining
 constant, (short term memory) or updating also
constant, (short term memory) or updating also  each time a new opinion is collected does not change the outcome of the
clustering process but changes the convergence time: constant
each time a new opinion is collected does not change the outcome of the
clustering process but changes the convergence time: constant  yields a fast exponential convergence, while varying
yields a fast exponential convergence, while varying  results in an hyperbolic convergence.
results in an hyperbolic convergence.
One can of course question the genericity of the results that were obtained
with such simple models. In fact the main result, namely clustering, would
not be canceled but rather re-inforced by two most direct generalisations
of the model:
-
A given population of agents might have a distribution of eventually conflicting
interests which could be translated in our formalism as initial clustering
of opinions or at least a non-uniform distribution.
-
Opinions can also result from the combination of hypotheses which can already
lead to different clusters because of conflicting interpretations.
We can then conclude that clustering into different opinions groups is
the rule as soon as openness is limited.
Acknowledgments:
We thank David Neau and the members of the IMAGES
FAIR project, Edmund Chattoe, Nils Ferrand and Nigel Gilbert for helpful
discussions. GW benefited at different stages in the project from discussions
with Sam Bowles, Winslow Farell and John Padgett at the Santa Fe Institute
whom we thank for its hospitality. Thanks to Rainer Hegselmann for pointing
us the references to the "consensus" literature. This study has been carried
out with financial support from the Commission of the European Communities,
Agriculture and Fisheries (FAIR) Specific RTD program, CT96-2092, "Improving
Agri-Environmental Policies : A Simulation Approach to the Role of the
Cognitive Properties of Farmers and Institutions". It does not necessarily
reflect its views and in no way anticipates the Commission's future policy
in this area.
References
Arthur, B. W. (1994) ``Increasing Returns and Path Dependence in the
Economy'', University of Michigan Press, Ann Arbor, MI.
Axelrod R. (1997) "Disseminating cultures" in Axelrod R., The complexity
of cooperation, Princeton University Press.
Chatterjee S. and Seneta E., (1977) "Towards consensus: some convergence
theorems on repeated averaging", J. Appl. Prob. 14, 89-97.
Cohen J. E., Hajnal J. and Newman C.M. (1986) "Approaching consensus
can be delicate when positions harden" Stochastic Processes and their
Applications 22, 315-322.
G. Deffuant, D. Neau, F. Amblard and G. Weisbuch (2000) "Mixing
beliefs among interacting agents" Advances in Complex Systems
3, 87-98.
Föllmer H. (1974) "Random Economies with Many Interacting Agents",
Journal of Mathematical Economics 1/1, 51-62.
Hegselmann R. and Krause U. (2002) "Opinion formation under bounded
confidence" proceedings of the Simsoc5 conference to appear in JASSS.
Henrich J., Boyd R., Bowles S., Camerer C., Fehr E., Gintis H., and
McElreath R. (2001) "In Search of Homo Economicus: Behavioral Experiments
in 15 Small-Scale Societies" Am. Econ. Rev. 91, 2, pp. 73-78
Higgs P.G. and Derrida, B. (1991) ``Stochastic models for species formation
in evolving populations'', J. Phys. A: Math. Gen. 24, 985-991.
Krause U. (2000) "A discrete non-linear and non-autonomous model of
consensus formation" in Communications in Difference Equations, Elaydi
etal edit. Gordon and Breach pub.
Laslier, J.F. (1989) ``Diffusion d'information et évaluations
séquentielles'' Economie appliquée.
Latané, B. and Nowak, A. (1997) "Self- Organizing Social Systems:
Necessary and Sufficient Conditions for the Emergence of Clustering, Consolidation
and Continuing Diversity", pp. 43-74 in Barnett, G. A. and Boster, F. J.
(eds.) Progress in Communication Sciences.
Neau, D (2000), ``Révisions des croyances
dans un système d'agents en interaction'', rapport d'option
de l'école polytechnique, available at http://www.lps.ens.fr/~ weisbuch/rapneau.ps.
Orléan A. (1995), "Bayesian Interactions and Collective Dynamics
of Opinions: Herd Behavior and Mimetic Contagion", Journal of Economic
Behavior and Organization, 28, 257-274.
Stauffer D. and Aharony A. (1994) "Introduction to Percolation Theory",
Taylor and Francis, London.
Stone M. "The opinion Pool" (1961) Ann. of Math. Stat. 32, 1339-1342.
Weisbuch G. and Boudjema G. (1999), ``Dynamical aspects in the Adoption
of Agri-Environmental Measures'', Adv. Complex Systems 2, 11-36.
Young H. P., and Burke M. A. (2001) "Competition and Custom in Economic
Contracts: A Case Study of Illinois Agriculture", Am. Econ. Rev.,
91, 3, pp. 559-573.
Footnotes
-
... Statistique1
-
Laboratoire associé au CNRS (URA 1306), à l'ENS et
aux Universités
Paris 6 et Paris 7
-
... mode2
-
The "consensus" literature most often uses parallel iteration mode when
they suppose that agents average at each time step the opinions of their
neighbourhood. Their implicit rationale for parallel iteration is that
they model successive meetings among experts.
-
... 2000)3
-
The other extreme is the absence of any threshold which yields consensus
at infinite time as earlier studied in Stone 1961 and others.
-
... 34
-
Notice the continuous transitions in the average number of clusters when
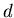 varies. Because of the randomness of the initial distribution and pair
sampling, any prediction on the outcome of dynamics such as the 1/2d rule
can be expressed as true with a probability close to one in the limit of
large
varies. Because of the randomness of the initial distribution and pair
sampling, any prediction on the outcome of dynamics such as the 1/2d rule
can be expressed as true with a probability close to one in the limit of
large  ;
but one can often generate a deterministic sequence of updates which would
contradict the "most likely" prediction.
;
but one can often generate a deterministic sequence of updates which would
contradict the "most likely" prediction.
-
... variance5
-
In fact adding the second term would compensate the decay in variance due
to the multiplication by
 in the limit of large
in the limit of large 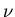 ;
for finite
;
for finite 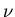 ,
partial compensation depends on the form of the distribution of opinions,
but anyway, variance decays exponentially with a smaller rate than when
,
partial compensation depends on the form of the distribution of opinions,
but anyway, variance decays exponentially with a smaller rate than when 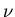 is close to 0
is close to 0
-
... share.6
-
The bit string model shares some resemblance with Axelrod's model of disseminating
culture (Axelrod 1997) based on adjustment of cultures as sets of vectors
of integer variables characterising agents on a square lattice.
Gerard Weisbuch
2001-11-26
![]() is the convergence parameter whose values may range from 0 to 0.5.
is the convergence parameter whose values may range from 0 to 0.5.
![]() is taken as constant in time and across the whole population. Note that
we here apply a complete mixing hypothesis plus a random serial iteration
mode2.
is taken as constant in time and across the whole population. Note that
we here apply a complete mixing hypothesis plus a random serial iteration
mode2.
![]() (Neau 2000)3.
Time variations of opinions' density
(Neau 2000)3.
Time variations of opinions' density ![]() obey the following dynamics:
obey the following dynamics:


![]() :
this is to be further referred to as the "1/2d rule" (see figure 34).
:
this is to be further referred to as the "1/2d rule" (see figure 34).

![]() .
.
![]() (
(![]() ,
all results displayed in this section are equilibrium results at large
times). As seen in figure 4, the lattice is filled with a large majority
of agents who have reached consensus around
,
all results displayed in this section are equilibrium results at large
times). As seen in figure 4, the lattice is filled with a large majority
of agents who have reached consensus around ![]() while a few isolated agents have ``extremists'' opinions closer to 0 or
1. The importance of extremists is the most noticeable difference with
the full mixing case described in the previous section.
while a few isolated agents have ``extremists'' opinions closer to 0 or
1. The importance of extremists is the most noticeable difference with
the full mixing case described in the previous section.



![]() by
by ![]() and the other agent's opinion
and the other agent's opinion ![]() by
by ![]() ,
with
,
with ![]() .
.![]() can be re-written
can be re-written ![]() where
where ![]() expresses a characteristic number of opinions taken into account in the
averaging process.
expresses a characteristic number of opinions taken into account in the
averaging process.![]() is then a relative weight of the agent previous opinion as compared to
the newly sampled opinion weighted
is then a relative weight of the agent previous opinion as compared to
the newly sampled opinion weighted ![]() .
Within this interpretation, updates of both opinion
.
Within this interpretation, updates of both opinion ![]() and variance
and variance ![]() should be written:
should be written:
![]() at time
at time ![]() to
to ![]() at time
at time ![]() .
It is directly obtained from the definition of variance as a weighted sum
of squared deviations.
.
It is directly obtained from the definition of variance as a weighted sum
of squared deviations.
![]() according to:
according to:
![]() connected to
connected to ![]() the number of previously collected opinions:
the number of previously collected opinions:
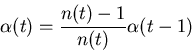
![]() constant which corresponds to taking a moving average on opinions and giving
more importance to the
constant which corresponds to taking a moving average on opinions and giving
more importance to the ![]() later collected opinions. Such a "bounded" memory would make sense in the
case when the agent believes that there exists some slow shift in the distribution
of opinions, whatever its cause, and that older opinions should be discarded.
later collected opinions. Such a "bounded" memory would make sense in the
case when the agent believes that there exists some slow shift in the distribution
of opinions, whatever its cause, and that older opinions should be discarded.
![]() corresponding to the same
corresponding to the same ![]() .
.
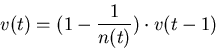
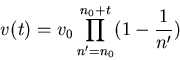
![]() and
and ![]() )
which are closer than those one could obtain with constant thresholds (typically
around
)
which are closer than those one could obtain with constant thresholds (typically
around ![]() and
and ![]() ):
initial convergence gathered opinions which would had aggregate at the
initial threshold values, but which later segregate due to the decrease
in thresholds. Many outliers are apparent on the plot.
):
initial convergence gathered opinions which would had aggregate at the
initial threshold values, but which later segregate due to the decrease
in thresholds. Many outliers are apparent on the plot.

![]() ,
the observed dynamics is not very different from what we obtained with
constant thresholds.
,
the observed dynamics is not very different from what we obtained with
constant thresholds.



![]() (which would yield consensus with only one cluster if kept constant) and
(which would yield consensus with only one cluster if kept constant) and ![]() (corresponding to
(corresponding to![]() ,
i.e. agents giving equal weight to their own opinion and to the external
opinion), more than ten clusters unequal in size are observed plus isolated
outliers. One way to characterise the dispersion of opinions with varying
,
i.e. agents giving equal weight to their own opinion and to the external
opinion), more than ten clusters unequal in size are observed plus isolated
outliers. One way to characterise the dispersion of opinions with varying ![]() is to compute
is to compute ![]() the relative value of the squared cluster sizes with respect to the squared
number of opinions.
the relative value of the squared cluster sizes with respect to the squared
number of opinions.

![]() and
and ![]() are small.
are small.
![]() ,
, ![]() ,
, ![]() and
and ![]() ,
the parameters of figure 11, we found that mainstream agents in the two
attractors account for 43 and 42 perc. of the population while 15 perc.
are in the minority peaks.
,
the parameters of figure 11, we found that mainstream agents in the two
attractors account for 43 and 42 perc. of the population while 15 perc.
are in the minority peaks.
![]() .
In this regime, corresponding to "insecure agents" who don't value their
own opinion more than those of other agents, we observe more clusters which
importance and localisation depend on the random sampling of interacting
agents and are thus harder to predict than in the other regime with a small
number of big clusters. Using a physical metaphor, clustering in this regime
resembles quenching to a frozen configuration, thus maintaining many "defects"
(e.g. here the outliers), while the opposite regime it resembles annealing
(with suppression of defects).
.
In this regime, corresponding to "insecure agents" who don't value their
own opinion more than those of other agents, we observe more clusters which
importance and localisation depend on the random sampling of interacting
agents and are thus harder to predict than in the other regime with a small
number of big clusters. Using a physical metaphor, clustering in this regime
resembles quenching to a frozen configuration, thus maintaining many "defects"
(e.g. here the outliers), while the opposite regime it resembles annealing
(with suppression of defects).

![]() .
.

![]() .
But continuous opinions display a regular decrease of cluster number with
.
But continuous opinions display a regular decrease of cluster number with ![]() while binary strings display a phase transition from consensus to a large
multiplicity of clusters.
while binary strings display a phase transition from consensus to a large
multiplicity of clusters.