Chapitre 10
Les réseaux booléens aléatoires
10-1 A LA RECHERCHE DES PROPRIETES GENERIQUES
Au cours des chapitres précédents nous avons essentiellement adopté une attitude d'ingénieurs: il s'est agi pour nous d'imaginer des recettes permettant de construire des réseaux exhibant un comportement donné, voire de rechercher les réseaux les mieux adaptés pour remplir une tâche déterminée. On peut reprendre le problème de la dynamique des réseaux d'une manière plus large en essayant de caractériser les propriétés d'un réseau "quelconque", non dédié, c'est-à-dire qui n'a pas été construit dans le but d'accomplir une tâche précise. Deux questions préalables se posent:
• Qu'est-ce qu'un réseau quelconque?
• Quelles propriétés étudier?
La notion de propriétés génériques dont nous abordons l'étude est une réponse possible à ces deux questions. En fait, on s'intéresse non pas aux particularités d'un réseau déterminé, mais aux ordres de grandeur que l'on s'attend à observer en étudiant un ensemble de réseaux dont les principes de construction sont fixés. On considère donc un ensemble comportant un nombre très grand, mais fini, de réseaux. On construit, par tirage au sort, plusieurs réseaux de l'ensemble et l'on mesure leurs propriétés dynamiques. On moyenne ensuite ces propriétés, et l'on s'intéresse à celles dont la distribution sur l'ensemble des réseaux n'est pas trop dispersée. Un exemple nous permettra de préciser ces idées.
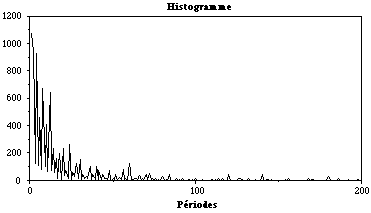
Considérons les réseaux booléens de connectivité donnée k = 2, dont la structure de connexions est aléatoire. La grandeur dynamique qui nous intéresse est la période sur l'ensemble des conditions initiales et des réseaux. Bien entendu cette période varie d'un réseau à l'autre. Nous en avons fait la mesure pour 10 conditions initiales tirées au hasard pour 1000 réseaux de 256 automates à connexions aléatoires, dont les fonctions de changement d'état ont été générées par tirage au sort en chaque site du réseau. La figure 10.1 montre l'histogramme des périodes. Il ressort de cet histogramme que l'ordre de grandeur de la période est de dix (c'est là la propriété générique), bien que la distribution des périodes soit assez large.
On peut certes construire sur mesure des réseaux "extrêmes" dont la période est inobservable avant un million d'itérations. Il suffit de prendre pour cela des réseaux ne contenant qu'un mélange aléatoire de fonctions OU exclusif et EQUivalence (c'est la fonction complémentaire de OU exclusif; elle ne donne 1 en sortie que si ses deux entrées sont égales). Mais ces cas extrêmes ne sont observés que pour une infime fraction de l'ensemble considéré: 1/7256. On les considère comme pathologiques, c'est-à-dire non représentatifs de l'ensemble étudié.

Figure 10.1
Histogramme des périodes pour 10 conditions initiales de 1000 réseaux booléens aléatoires de 256 automates.On appelle donc propriétés génériques d'un ensemble de réseaux celles qui sont indépendantes de la structure détaillée du réseau; on les retrouve sur la quasi-totalité des réseaux de l'ensemble. La notion s'applique donc aux réseaux de construction aléatoire. Les propriétés génériques peuvent ne pas être vérifiées par quelques cas pathologiques dont la proportion tend rapidement vers 0 lorsque augmente la taille du réseau. En général les propriétés génériques sont :
• soit des propriétés qualitatives dont la probabilité d'être vraies (ou fausses, suivant les cas) est proche de 1;
• soit des propriétés semi-quantitatives, comme les lois d'échelle reliant les propriétés dynamiques au nombre des automates.
Ce chapitre est consacré à l'étude des propriétés génériques des réseaux booléens aléatoires. Nous y trouverons donc un grand nombre d'exemples de propriétés génériques.
L'idée de propriété générique caractérisant les réseaux de construction aléatoire est à la base des modèles de biologie théorique que nous décrirons au chapitre 11. Elle a été considérablement développée par les physiciens des systèmes désordonnés pour l'étude de systèmes aléatoires microscopiques comme les verres, ou de systèmes multiphasiques macroscopiques. Beaucoup de notions nouvelles ont été découvertes (ou redécouvertes) par eux durant les années 70. La notion de propriétés génériques s'apparente en effet à celle des classes d'universalité, développée pour les transitions de phase. Sans entrer dans trop de détails, on peut dire que les grandeurs physiques impliquées dans les transitions de phases obéissent à des lois d'échelle qui peuvent être indépendantes de la transition considérée (il peut s'agir aussi bien de problèmes de magnétisme, de supraconductivité ou de physico-chimie) comme des détails du modèle mathématique choisi. Ces lois ne dépendent que de la dimension physique de l'espace dans lequel s'effectue la transition (pour nous l'espace à trois dimensions) et de la dimension du paramètre d'ordre. L'ensemble des transitions de phase (et de leurs modèles mathématiques) obéissant aux mêmes lois d'échelle constitue une classe d'universalité. Cette notion de classe d'universalité a d'ailleurs été étendue aux transitions de régime concernant les systèmes dynamiques continus.
En fait la première proposition de modéliser un système biologique par un réseau désordonné d'automates, due à S. Kauffman, un théoricien de la biologie, est antérieure à l'intérêt des physiciens pour le sujet. Elle est, elle aussi, basée sur l'idée que les propriétés des systèmes désordonnés sont représentatives de la très grande majorité des systèmes définis par une même structure moyenne.
10-2 LOIS D'ECHELLE DES PERIODES
Stuart Kauffman s'est intéressé dès la fin des années soixante aux propriétés dynamiques des réseaux booléens aléatoires. Il a donc construit des réseaux d'automates booléens de connectivité d'entrée quelconque k. La fonction de changement d'état de chaque automate est tirée au sort parmi les 2 puissance 2k fonctions possibles. Les connexions entre automates sont elles aussi tirées au sort. Le réseau est dit à connectivité aléatoire, par opposition aux réseaux cellulaires par exemple.
On s'intéresse essentiellement aux propriétés statistiques de ces réseaux dont la taille, et surtout l'espace des états, sont importants. Par conséquent, il n'est pas question d'en établir le graphe d'itération complet. Pour étudier les attracteurs d'un réseau donné, on tire au sort un nombre important de configurations initiales. A partir de chacune d'elles, on laisse évoluer le réseau vers un attracteur. On sauvegarde certaines configurations, dites de référence, à des temps croissant suivant une progression géométrique de raison 2, et la première coïncidence de la référence avec une configuration prise à un instant ultérieur indique que le cycle limite est atteint. La période du cycle limite est obtenue en notant le plus court intervalle de temps séparant deux passages successifs par la configuration de référence. Cette configuration de référence est alors la seule à être sauvegardée. On peut ainsi savoir si les cycles limites sont distincts en comparant, lors de la recherche du cycle limite, la configuration courante à l'ensemble des configurations de référence déjà obtenues.
Les résultats obtenus par Kauffman mettent en évidence deux régimes dynamiques distincts suivant la connectivité:
Pour des réseaux de connectivité 2, la période moyenne varie comme la racine carrée du nombre des automates N. Il en est de même du nombre des attracteurs (voir plus loin la figure 11.1). Autrement dit, parmi les 2N configurations a priori possibles pour le réseau, la dynamique n'en sélectionne qu'un petit nombre de l'ordre de N, qui sont réellement accessibles au système après la période transitoire. Cette sélection peut s'interpréter comme une propriété d'organisation du réseau.
Lorsque la connectivité augmente, la période augmente beaucoup plus vite avec le nombre des automates: dès que la connectivité atteint 4, la loi de variation de la période, de même que celle concernant le nombre des attracteurs, devient exponentielle en fonction du nombre des automates. Ces périodes, très grandes dès que le nombre des automates dépasse la centaine, ne sont même plus observables et rappellent le comportement chaotique des systèmes continus apériodiques. Par contraste avec le régime organisé, l'espace des états accessibles reste important, même dans la limite des grands temps. Nous verrons plus loin que d'autres propriétés dynamiques rapprochent ces systèmes discrets des systèmes continus chaotiques et nous appellerons donc chaotique le comportement caractérisé par les grandes périodes.
Les lois d'échelle reliant la période et le nombre des attracteurs au nombre des automates sont des propriétés génériques des réseaux booléens aléatoires. Elle ne dépendent que de la connectivité du réseau. Il est certes possible de construire des contre-exemples pathologiques: si l'on construit un réseau de connectivité 2 en n'utilisant que des fonctions OUex et EQUivalence, la période varie comme une exponentielle du nombre des automates. Mais l'ensemble des réseaux ainsi construits ne représente qu'une infime fraction de l'ensemble des réseaux booléens aléatoires. De ce fait, la propriété est bien générique.
La différence des lois d'échelles en fonction de la connectivité est l'indication de comportements dynamiques très différents dans les deux cas. Nous allons introduire dans ce chapitre toute une série de tests, qui sont autant de propriétés génériques, permettant de mettre évidence la différence entre les deux régimes dynamiques.
Le cas de la connectivité complète
Malgré vingt ans d'essais infructueux, les résultats de Kauffman ne sont toujours pas démontrés. Seuls les deux cas extrêmes, k = 1 et k = N, sont bien compris.
• Pour k = 1, les réseaux sont constitués de "crabes" indépendants dont la dynamique a été exposée au chapitre 2 (2.2.3).
• Pour k = N, le cas de la connectivité complète, l'état de chaque automate dépend de tous les autres, y compris de lui-même. Pour spécifier les règles de changement d'état, il faut et il suffit d'écrire le tableau complet des M = 2N successeurs de chacun des états du système. On peut alors interpréter chaque configuration comme la représentation binaire d'un entier compris entre 0 et M-1. Le problème posé est donc équivalent au problème de l'application d'un ensemble fini de M entiers sur lui-même.
Pour un réseau aléatoire, le tableau des successeurs tout comme le graphe d'itération est entièrement aléatoire: la probabilité qu'une configuration quelconque succède à une autre est de 1/ M .
Considérons le sous-graphe d'itération
C0 ----> C1----->C2---..............--->Ci---..............--->Ck-1
qui part d'une configuration C0 et aboutit après k-1 itérations à la configuration Ck-1, et tel que toutes les configurations C0, Ci, Ck-1 soient différentes. P(k), la probabilité de ce sous-graphe, est donnée par le produit des probabilités que chacune des i configurations soit différente des i-1 précédentes:
P(k) = (1-1/M).(1-2/M).(1-3/M)...................(1-(k-1)/M) (10.1)
P(k), produit de termes inférieurs à 1, est lui-même inférieur à 1; pour k petit, P(k) est proche de 1. En fait, en passant par le calcul de son logarithme, on peut approximer P(k) par une gaussienne:
![]()
![]()
Cette expression est valable pour 1 << k << M.
La probabilité d'une configuration quelconque, appartenant ou non au sous-graphe, d'être la configuration Ck suivant Ck-1 est donc P(k)/M. C'est le cas en particulier de C0. P(k)/M est donc la probabilité que C0 appartienne à un cycle de longueur k. n(k), le nombre moyen des cycles de longueur k, est donc:
n(k) = (10.3)
c'est-à-dire le nombre moyen de points appartenant à un cycle de longueur k, divisé par la longueur du cyle. La distribution des cycles est donc fortement déplacée vers les petits cycles. Il existe en moyenne un cycle de longueur 1.
Le nombre total de cycles correspond à la sommation des n(k) pour k augmentant jusqu'à M. On démontre que cette somme tend vers Log(M)/2, c'est-à-dire N (Log2/2). (On peut approximer cette limite en remarquant que la gaussienne a pour largeur . L'ordre de grandeur de la somme est donc obtenu en sommant la série harmonique en 1/k jusqu'à k = .)
La première loi d'échelle s'énonce donc ainsi: le nombre des attracteurs varie linéairement avec celui des automates.
A partir d'une configuration C0 quelconque, la probabilité que la boucle se referme en Ci, donnant une période de longueur k-i est toujours P(k)/M. Cette probabilité est en particulier indépendante de i. On obtient donc la longueur moyenne d'un cycle par une double somme sur i et k, de la période k-i pondérée par la probabilité P(k). En approximant les sommes par des intégrales et P(k) par la gaussienne, on obtient:
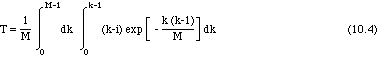
![]()
On obtient ainsi un terme proportionnel à .
La période moyenne varie donc comme une fonction exponentielle du nombre des automates:
T = a 2N/2 (10.5)
C'est la deuxième loi d'échelle. a vaut 0,63.
Enfin, l'ensemble de ces deux résultats indique que la fraction de l'espace des configurations occupée par les attracteurs est importante.
Il n'existe malheureusement aucun résultat analytique exact s'appliquant aux cas intermédiaires, pour les connectivités comprises entre 1 et N.
10-3 LES RESEAUX CELLULAIRES A FONCTIONS ALEATOIRES
L'étude des réseaux inhomogènes à connectivité cellulaire permet de visualiser simplement l'état des automates au cours des itérations et ainsi de mieux comprendre la dynamique des réseaux aléatoires. H. Hartman et G. Vichniac, deux auteurs du M.I.T., ont proposé de nommer INCA (pour INhomogeneous Cellular Automata) les structures de connexions périodiques pour lesquelles la fonction de l'automate varie en chaque nœud.
Les INCA à une dimension peuvent être constitués par une chaîne linéaire avec interaction entre proches voisins. Une structure très simple est la chaîne d'automates à 2 entrées dont nous avons parlé au chapitre 3 (3.3).
La figure 10.2 montre l'évolution d'un INCA linéaire constitué d'un mélange aléatoire de 30% de fonctions OU et de 70% de fonctions OUex. Dans cette étude, comme dans les suivantes sur les réseaux à deux dimensions, les conditions aux bords sont périodiques: l'automate de l'extrémité droite de la chaîne est connecté à l'automate de l'extrémité gauche. La première ligne indique la fonction de chacun des automates: O figure la fonction OU et X la fonction OUex (XOR en anglais). Les lignes suivantes indiquent l'état du réseau à chaque intervalle de temps, le temps croissant vers le bas. Les étoiles * figurent les automates à l'état 1, les points . ceux à l'état 0. Rappelons (voir le chapitre 3) qu'un réseau linéaire d'automates à deux entrées se divise en deux sous-réseaux indépendants lorsque le nombre des automates est pair. La figure 10.2 ne représente donc qu'un seul de ces sous-réseaux.
Les rectangles grisés entourent des sous-réseaux de nœuds qui restent invariants au cours de l'itération, après une période transitoire variable suivant le sous-réseau. Ces murs grisés isolent des parties oscillantes. Les parties blanches oscillent indépendamment les unes des autres, les murs stables bloquant toute transmission de signal entre les parties oscillantes. On peut mesurer sur la figure les périodes des sous-réseaux oscillants: en partant de gauche à droite, on trouve 10, 4 et 6. La période du réseau est donc leur plus petit commun multiple, 60.

Figure 10.2
L'origine des murs stables se comprend aisément sur cet exemple. Dès qu'une paire de fonctions OU voisines occupe la configuration 11, elle reste indéfiniment dans cette configuration. En effet, pour qu'une fonction OU reste dans l'état 1, il suffit qu'une seule de ses entrées y soit maintenue. La fonction OU est une fonction forçante, dont l'état est fixé par une seule de ses entrées. Cet état est l'état forcé et l'entrée qui permet cette opération est l'entrée forçante. Les deux entrées d'une fonction OU sont forçantes.
Une paire de fonctions OU voisines est une structure forçante: car chaque état forcé d'une cellule est l'état forçant de l'autre. Les structures forçantes s'étendent à partir des paires de fonctions OU, ainsi qu'on peut le voir sur la figure 10.2 .
Lorsqu'on augmente la taille du réseau, la taille des parties oscillantes n'augmente que très lentement, de même que leur période. De ce fait, l'augmentation de la période du réseau avec la taille est lente elle aussi.
En conclusion, l'organisation temporelle du réseau suivant des cycles de périodes courtes est liée à son organisation spatiale en sous-réseaux oscillants séparés par des murs stables, et l'existence des murs stables est due aux structures forçantes. Cette conclusion reste valable pour n'importe quel mélange aléatoire de fonctions boolénnes à deux entrées.
10-3-1 Structuration fonctionnelle
Le même type d'observations peut se faire sur une structure cellulaire bidimensionnelle, représentée figure 10.3, pour laquelle la structure des connexions varie alternativement d'un site à son voisin.
Figure 10.3
Les fonctions de changement d'état sont tirées au sort parmi les 14 fonctions booléennes à deux entrées non constantes (à l'exclusion des fonctions constantes à l'état 0 ou 1). La figure 10.4 représente quatre configurations d'un même réseau appartenant à des cycles limites obtenus à partir de conditions initiales différentes.
En deux dimensions on observe donc aussi la structuration spatiale caractéristique des réseaux de période courte. En fait, le lien entre courtes périodes et organisation en sous-réseaux fonctionnellement indépendants n'est pas dû à la structure cellulaire. Il existe aussi pour les réseaux à connexions aléatoires d'automates booléens à deux entrées: en l'absence d'une représentation bidimensionnelle, on peut vérifier à l'ordinateur le caractère non connexe de l'ensemble des nœuds oscillants lors du cycle limite.
. 0 0 0 . . * . 0 1 * . 1 0 1 * . 1 1 1 . . * . 0 1 * . 1 0 1 *
* 0 1 0 1 0 . . 0 1 * . 1 1 1 1 * 0 1 0 1 0 . . 1 1 * . 1 0 1 0
0 . . 0 0 0 0 . . 0 1 1 * 0 1 1 0 . . 1 1 0 1 . . 0 1 1 * 0 1 1
. . 0 0 1 0 0 * * 1 1 0 * . * . . . 0 0 1 0 0 * * 0 1 1 * . * .
* * 0 1 * . 0 0 . 0 * * . * * . * * 1 0 * . 0 0 . 0 * * . * * .
. 0 0 0 . . 0 1 . * 1 0 * . . * . 0 0 0 . . 0 0 . * 1 1 * . . *
. . * 0 . * 0 0 1 . 1 1 1 . . . . . * 0 . * 0 0 1 . 1 1 1 . . .
. 1 0 0 . 1 0 . * 0 0 * 1 . . . . 0 0 1 . 0 0 . * 1 0 * * . . .
0 1 1 1 0 1 1 0 0 * * * 1 0 * 1 . 1 0 1 1 1 1 0 0 * * * * * * .
1 * 0 . 0 1 1 0 1 1 . 1 1 1 0 0 * * . . 0 1 1 1 1 0 . * . * * .
0 0 1 * 1 0 0 1 * . 1 0 . 1 1 1 . * * * 1 0 0 1 * . 1 1 . . * .
1 1 * * 0 1 0 . * * 0 0 * 1 1 0 . * * * 0 1 0 . * * 0 1 * * . .
* . * * 0 0 0 * . . . 0 0 1 0 . * . * * 0 0 0 * . . . 1 0 1 1 .
* * * . * . . . * . * . 1 0 . * * * * . * . . . * . * . 1 0 . *
. * . . . * . * * * . 1 0 1 . . . * . . . * . * * * . 0 1 1 . .
* . . * * * * * * . . 1 1 . . . * . . * * * * * * . . 1 1 . . .
. 0 1 0 . . * . 1 0 * . 1 1 1 * . . * . . . * . 1 0 * . 0 1 0 *
* 0 0 0 0 0 . . 1 1 * . 0 1 0 1 * . * . * . . . 0 0 * . 0 1 1 1
0 . . 0 1 0 1 0 . 1 1 1 1 1 1 0 1 . . . * . * 1 . 0 1 1 1 1 0 0
. . 1 0 0 0 0 1 1 0 0 1 1 0 * . . . . . * . . 1 0 1 0 0 0 0 * .
* * 1 1 * . 0 0 0 1 1 0 0 * * . * * * * * . 0 0 0 0 1 0 0 * * .
. 0 1 0 . . 1 0 0 1 0 1 1 . . * . . . . . . 1 1 1 1 1 0 0 . . *
. . * 0 . * 0 0 1 . 1 0 1 . . . . . * . . * 0 1 1 . 1 0 1 . . .
. 1 0 0 . 0 1 . 1 1 1 * 1 . . . . 0 1 1 . 1 1 . 0 0 0 * 1 . . .
0 0 1 0 0 1 1 1 0 * * * 0 1 * 0 0 0 1 0 0 0 1 1 0 * * * 0 1 * 0
1 * 0 . 1 1 0 1 0 0 . 1 0 1 1 0 1 * 0 . 1 0 0 0 1 1 . 1 0 1 1 0
1 1 0 * 1 1 0 0 * . 1 1 . 0 0 0 1 1 0 * 1 1 0 0 * . 1 1 . 0 0 0
0 1 * * 0 0 1 . * * 0 1 * 1 0 0 0 1 * * 1 1 0 . * * 0 1 * 1 0 0
* . * * 0 1 0 * . . . 1 0 1 0 . * . * * 0 1 0 * . . . 1 0 1 0 .
* * * . * . . . * . * . 0 0 . * * * * . * . . . * . * . 1 1 . *
. * . . . * . * * * . 0 0 1 . . . * . . . * . * * * . 0 1 1 . .
* . . * * * * * * . . 0 0 . . . * . . * * * * * * . . 1 1 . . .
Figure 10.4
Cycles limites d'un réseau booléen aléatoire 16516. Ces configurations sont obtenues en partant de quatre configurations initiales différentes. Les 0 et les 1 correspondent à des nœuds oscillants, les étoiles * et les points . , à des nœuds fixes lors du cycle limite, respectivement à l'état 1 et 0.10-3-2 Les paliers
La structure spatiale dépend des conditions initiales, ainsi que le montre la figure 10.4. Suivant celles-ci, certains nœuds oscillent ou restent fixes. On peut analyser cette dépendance en évaluant la probabilité d'osciller de chacun des nœuds sur l'ensemble des conditions initiales. La figure 10.5 a été obtenue à partir du même réseau que la figure 10.4. Pour 999 conditions initiales tirées au hasard, on a sommé pour chacun des nœuds le nombre de fois pour lesquelles le nœud oscille lors du cycle limite.
Sur cette figure, les 0 correspondent aux nœuds immobiles lors du cycle limite; leur ensemble constitue le noyau stable. Les 999 correspondent aux nœuds qui oscillent toujours. Les valeurs intermédiaires sont regroupées par paliers correspondant à des groupes de nœuds voisins: 31, 62, 63, 155, 407, 533, 564, 655, 717, 749, 780, 782, 875, 905, 936, 937. Ces paliers discontinus donnent des indications sur le nombre des cycles limites différents et sur la taille de leurs bassins d'attraction.
31 533 533 533 0 0 0 0 999 999 0 0 999 999 999 31
31 533 533 533 533 533 0 0 999 999 0 0 905 999 999 999
999 0 0 533 533 564 564 749 0 999 936 936 717 936 999 999
0 0 564 564 533 564 564 749 749 999 936 936 655 655 0 0
0 0 564 564 0 0 999 999 749 999 718 655 655 0 0 0
0 564 564 564 0 0 999 999 749 749 936 936 655 0 0 0
0 0 0 564 0 0 999 999 999 62 936 936 936 0 0 0
0 999 999 999 0 999 999 62 780 936 936 62 407 0 0 0
438 999 999 999 999 999 999 999 999 62 62 62 438 438 0 438
438 0 438 0 999 999 999 999 999 999 62 438 438 438 438 438
438 438 438 0 999 999 999 999 63 63 782 782 0 438 438 438
438 438 0 0 999 999 999 0 63 63 782 782 0 438 438 438
31 155 155 0 999 999 999 0 63 63 0 782 782 937 937 31
31 155 155 155 0 0 0 0 63 63 0 0 999 999 0 31
31 0 0 0 0 0 0 0 0 0 0 875 999 999 31 31
0 0 0 0 0 0 0 0 0 0 0 875 875 31 31 31
Figure 10.5
Statistique des conditions initiales au cours desquelles les nœuds du réseau oscillent (la statistique porte sur 999 conditions initiales).10-3-3 Les structures forçantes
Les structures forçantes sont responsables de l'apparition du noyau stable. Sur les 14 fonctions booléennes utilisées, 12 sont des fonctions forçantes qui restent fixes si l'une de leurs entrées est fixée à la valeur forçante.
![]()
Figure 10.6
Un arc forçant.La structure représentée sur la figure 10.6 est un arc forçant: la sortie forcée de la fonction OU de gauche est aussi la valeur forçante de la fonction OU de droite.
La figure 10.7 représente une boucle forçante, où chaque fonction force la suivante. Toutes les boucles de quatre fonctions forçantes ne sont pas des boucles forçantes: encore faut-il que la successsion des valeurs forcées et forçantes s'effectue dans le bon ordre. Nous retrouvons ici des notions qui généralisent la notion de frustration introduite pour la connectivité 1 au chapitre 2. Les boucles forçantes généralisent la notion de boucle non frustrée; elles sont les germes du noyau stable. D'autres éléments s'y agglutinent de manière transitive: fonctions forçantes dont une des entrées forçantes est liée à la boucle forçante, ou même fonctions non forçantes dont les deux entrées sont fixées par leurs liens avec la boucle forçante.
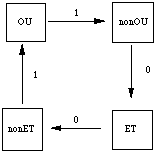
Figure 10.7
Une boucle forçante.L'existence de noyaux stables, et par voie de conséquence des périodes courtes, dépend de la proportion de fonctions forçantes. Pour une connectivité de 1, toutes les fonctions sont forçantes. Nous avons déjà vu au paragraphe 2.2.3 que ces réseaux étaient toujours structurés en sous-réseaux et que leurs périodes étaient courtes. Si la connectivité est de 2, 14 des 16 fonctions booléennes sont des fonctions forçantes: les réseaux aléatoires ont donc des périodes courtes et sont structurés. En revanche, dès la connectivité 4 la proportion de fonctions forçantes tombe à 4%, d'où l'absence de structures forçantes et de structuration, et la présence de grandes périodes.
10-3-4 La transition de phase
Le paramètre connectivité ne prend que des valeurs entières. Il est intéressant d'introduire un paramètre continu pour suivre la transition entre les deux régimes, le régime organisé pour les basses périodes, et le régime chaotique correspondant aux périodes élevées. B. Derrida et D. Stauffer ont proposé de travailler sur des réseaux carrés d'automates booléens à quatre entrées. La figure 10.8 montre la structure des connexions.
Le paramètre continu p est la probabilité que la sortie de l'automate soit 1 pour une configuration d'entrée donnée. Autrement dit, les réseaux sont construits de la manière suivante. On remplit les tables de vérité de chacun des automates par un tirage au sort qui affecte des 1 en sortie avec une probabilité p. Si p = 0, tous les automates sont invariants et les sorties valent toutes 0; si p = 1, tous les automates sont invariants et les sorties valent toutes 1. Les valeurs intéressantes de p sont bien sûr les valeurs intermédiaires. Du fait de la symétrie entre 0 et 1, p = 0,5 est un point de symétrie du point de vue des comportements. Il suffit donc d'étudier les comportements sur l'intervalle [0 , 0,5 ]. Si p = 0,5 , le tirage correspond à l'équipartition entre toutes les fonctions booléennes de connectivité quatre; nous nous attendons donc au comportement chaotique annoncé par Kauffman. Par contre, pour les valeurs de p proches de 0, on s'attend à des configurations attractrices composées essentiellement de 0 entre lesquels oscillent quelques automates; donc à un comportement organisé. Quelque part entre ces comportements extrêmes, un changement de régime doit se produire. La valeur critique de p est de 0,28. En dessous de cette valeur on observe des périodes petites qui croissent comme une puissance du nombre des automates du réseau. Au-dessus de p = 0,28 la croissance de la période est exponentielle.
Figure 10.8
L'examen des périodes locales est également intéressant. Chaque automate oscille, ou non, avec une certaine période au cours du cycle limite. La période du réseau est le plus petit commun multiple de toutes ces périodes. Les figures 10.9 et 10.10 montrent ces périodes.
1 1 4 4 8 8 8 1 1 4 4 1 1 1 1 1
1 1 1 1 8 8 4 1 1 1 1 1 1 4 1 1
4 1 1 1 8 72 4 1 1 1 1 1 1 4 1 4
4 1 1 72 72 36 4 1 2 1 1 1 1 1 1 1
4 4 1 18 1 18 36 2 2 2 1 1 1 1 6 1
4 1 1 18 18 18 36 1 1 1 1 1 1 12 6 12
12 1 18 18 18 18 18 1 1 1 1 1 12 12 1 12
1 1 18 18 18 1 18 1 1 1 1 1 1 12 12 12
1 1 1 1 1 1 1 1 1 4 4 1 12 12 1 1
1 1 1 1 1 1 1 1 1 1 4 4 4 12 1 1
1 4 4 1 1 1 1 1 1 1 4 4 1 4 1 4
1 1 1 1 1 1 1 1 1 1 1 4 1 4 4 4
1 1 1 1 2 2 1 1 1 1 1 1 1 1 4 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 1
1 1 1 8 8 1 1 1 1 1 1 4 4 1 1 1
1 1 8 8 8 8 1 1 1 1 4 1 1 4 4 1
Figure 10.9
Périodes locales d'un réseau dans le régime organisé. p = 0,2 .On peut voir sur la figure 10.10, dans le cas du régime chaotique, que certains nœuds ont de très grandes périodes que la durée de la simulation ne permet pas d'observer. Les autres nœuds ont des périodes relativement réduites.
1********* 1 1 1 1 1 1 1 1 1 6 6 1
1****************** 1 1 1 1***************
*************************** 1 1 1 1****** 1
****************** 1 1*** 1 1 1 1****** 1
****************** 1*************** 1*********
*************** 2 2 2 2*** 4*** 1*********
************ 1 1 1 2 1 1******************
********* 1 1 1 1 1 1 1******************
********* 1 1 1 1 1 1*********************
*************** 1 1 1****************** 1***
************ 1 1 1 1************************
*** 1 1*************************** 1*********
*** 1 1*************************** 1*** 1 1
1 1 1*************************** 12*** 12 1
1 1************************ 1 1 12 6 6 1
1 1****** 1 1****** 1 1 1 1 1 2 6 1
Figure 10.10
Périodes locales dans le régime chaotique. p = 0,3 . Les groupes de trois étoiles *** correspondent aux nœuds dont la période est trop grande pour être mesurée.10-3-5 La percolation
La notion de percolation est importante dans l'étude des propriétés génériques des réseaux cellulaires désordonnés. On dit qu'une région homogène (par rapport à une certaine propriété, sur la figure 10.10 la région des automates de grande période) percole, si on peut passer d'un bord à l'autre du réseau en restant à l'intérieur de la région. Sur la figure 10.10 la région des grandes périodes percole, isolant les régions de basses périodes. Sur la figure 10.9 c'est la région des automates fixes qui percole. Si un ensemble percole, l'ensemble complémentaire n'est plus connexe.
. 3 3 3 3 1 . 3 3 9 9 9 9 9 . . . . . . 7 7 7 . . . 9 . . .
. . . 3 3 3 3 3 3 3 1 . 9 . . . . . . . 7 7 7 7 . 9 9 7 . 2
2 . . . . 3 . 3 3 3 3 3 . . . . . . . 9 9 . . 7 7 7 6 9 . .
. . . . 3 3 3 . . . 8 3 8 8 . 6 6 . . . 9 2 2 . 7 7 8 9 . .
. . . . 3 9 . . . 3 8 8 8 6 . . 1 . . . . 2 2 2 7 . 8 . . .
. . . . . 9 . . . 3 . . 8 . 5 5 3 . . . . . . . . 9 . . . .
. . . . . . . . . . . . . . 5 5 4 . . . . . 4 4 . 9 9 9 9 .
. . . . . . . . . 2 . . 2 . . . 4 1 . 4 4 4 . 4 9 9 . . . .
. . . . . . 9 9 . 2 2 2 2 . . . . 4 4 4 4 4 9 9 9 9 . . . 9
. 9 9 . . 9 9 9 . 2 2 . . . . . . . 4 4 . . 9 4 . . . . . 9
9 9 9 . . . 9 . 2 2 . . . . . . . . 4 . . . 9 9 . . . . . .
9 9 9 9 . . 9 . . 2 . . 4 4 . . . . 4 . . . 9 9 . . . . . .
9 9 9 . 9 9 7 . . . . . 4 4 . . . . 4 9 . 9 9 . . . 9 . . 9
9 . . . . . 2 . . . . . . . . . 9 9 9 9 8 8 3 . . . 9 . . 9
9 . . . 1 2 2 . . . 9 9 . . 9 9 9 9 9 8 8 . 1 1 . 9 9 . 9 9
. . 1 . 1 . . . . . 9 . . . 9 9 . 9 9 8 . . . . . 9 9 . . 9
9 . 1 1 1 . . . 9 9 9 . . . 9 9 9 9 7 9 9 9 . . 9 9 9 . . 9
9 9 7 4 2 2 . . 9 . 9 9 . . . 9 9 9 9 9 9 9 . 9 9 . . . 1 1
. 9 9 9 . . . . 9 . 1 9 9 . . . . . 9 9 . 9 . 9 9 9 . . 5 .
. . 8 6 . . . . 9 . 1 9 . . . . . . 9 9 . 9 9 . 9 9 9 9 4 5
5 3 5 2 2 . . . . . . . . . . . . . . 9 . 9 9 9 . . . . 9 5
5 . . . . . . . . . . . . . . . . . . 9 . . . . . . . . 9 5
5 . . . . . . . . . . . 9 9 . . . . 9 9 9 . . . . . . . 9 9
. 9 9 . 9 9 . . . . . . 9 . . . 9 9 9 9 . . . . . . . . . .
. 9 9 9 9 . . . . . . . 9 9 . . . . 9 9 . . . . . . . . . 9
9 . 9 9 9 9 . . . . . . 9 . . . . . 9 9 . . . . . . . . . 9
9 . 9 9 9 . . . . . 9 . 9 9 . . . . 8 9 . . . . . . . 9 9 9
9 9 9 9 . . 9 . . . 9 8 9 8 . . . . . . . . . . . . . . 9 .
. . . 9 . . 9 . . . . 8 8 8 . . . 9 9 9 9 9 9 9 . . . 9 9 .
. . . 3 . 9 9 9 3 . . . 9 9 9 . . 9 . . 7 7 7 9 . . 9 9 9 .
Figure 10.11
Statistique d'oscillation pour un réseau booléen aléatoire dans le régime organisé (p = 0,21). On observe la percolation du noyau stable, représenté par les points.La percolation du noyau stable est un bon test de la nature organisée ou chaotique de la dynamique du réseau. Les figures 10.11 et 10.12, correspondant à deux réseaux aléatoires avec p = 0,21 pour le premier et 0,28 pour le second, montrent la statistique des nœuds oscillants pour 9 conditions initiales. Les nœuds stables sont figurés par des points. Sur la figure 10.11 on observe la percolation du noyau stable. Les parties oscillantes sont donc isolées. Par contre, pour p = 0,28 , c'est l'ensemble des nœuds oscillants qui percole de haut en bas (mais pas de droite à gauche!). On peut noter aussi que la quasi-totalité des nœuds oscillants, sauf 8, appartiennent au même ensemble connexe. L'étude statistique de la percolation du noyau stable en fonction de p pour des réseaux de taille croissante permet de déterminer le seuil de percolation au-dessus duquel le noyau stable percole dans un réseau dont la taille tend vers l'infini: pc = 0,28 ± 0,02. Bien entendu, par raison de symétrie, on retrouve un comportement organisé au-dessus de p = 0,72.
. . . . . . . . . . 9 9 9 9 2 9 9 9 8 6 6 6 1 9 9 7 . . . .
. . 3 3 3 . . 9 . . . . 9 9 9 9 9 9 6 5 6 6 6 . . . . . . 1
. . . . . . . 9 9 9 . . 9 9 9 9 9 9 7 6 6 . . . . 9 . . . 1
. . . 9 . 3 9 9 9 . 9 9 9 9 9 9 9 9 8 8 6 2 . . . 9 9 9 9 .
. . . 9 3 3 3 . . . 9 9 9 9 9 9 9 9 9 9 6 2 . . . 9 9 9 9 9
. . . 8 . . . . . . 9 9 9 9 9 9 8 9 9 9 8 9 9 9 9 9 9 8 8 9
. . . 1 1 1 1 1 1 9 9 9 9 9 9 8 9 8 9 8 5 8 9 9 5 9 9 9 9 9
1 . . . 1 1 1 1 1 8 8 9 9 9 9 9 9 9 9 9 9 9 6 9 9 9 . . 9 9
9 9 . . . . 3 3 3 2 9 9 9 3 3 6 9 7 9 9 9 5 2 9 9 9 . . 9 9
1 1 1 . . . 3 3 3 3 3 9 3 3 3 . . . . . 9 9 2 9 7 9 9 . . .
1 . 1 . . . 3 3 9 9 3 3 . 3 . . . . . . 9 9 . 9 9 . 9 9 . .
. . . . . . 3 9 9 8 3 3 3 3 2 8 . . 9 9 9 9 9 9 9 9 9 9 9 9
9 . 9 9 . . . 1 1 9 9 3 3 3 2 8 . . . 9 9 . . 9 9 9 9 9 9 9
9 9 9 9 . . . 1 . 8 9 8 3 . 8 8 . . . 9 . . . . . 9 9 9 . 9
9 9 9 9 . 9 9 9 9 9 9 8 8 8 8 1 1 . 5 . . . . . . . . . . .
9 9 9 9 . 9 9 9 9 9 9 8 8 8 . 1 1 . 5 . . 9 9 9 . . . . . .
9 7 9 9 9 . . . 8 9 2 8 9 8 . . . . 8 . . 3 8 . . 2 7 2 2 .
9 9 . . 9 9 . . 9 8 8 8 9 8 8 . . 9 9 9 9 3 9 . . 7 6 6 . 9
9 7 7 . . . . . 9 9 8 8 9 9 . . . 9 9 9 9 9 9 9 . . 6 6 9 9
9 9 . . . 9 9 9 9 8 9 8 8 9 . . . 9 9 9 9 9 9 8 . 9 6 6 . 4
. . . . 9 9 9 9 9 9 9 8 9 9 9 9 9 9 9 9 9 9 8 9 9 9 9 6 . 4
. . . . 9 9 8 9 9 7 8 9 9 9 9 7 . . 9 9 9 9 9 9 9 1 . 6 . .
. . 9 9 . 9 9 9 9 8 8 9 . . . . . . . 9 9 . . 9 . 1 3 . . .
. . 9 . . 7 7 9 . . 6 9 . . . . . . . 9 9 . . 9 . 2 3 3 3 .
. . . . 7 7 7 2 9 9 1 1 . . . . . . . . . . . 9 . 2 3 3 . .
. . . . 7 7 7 3 9 . 2 . . . . . . . . . . . . 1 . 3 9 3 3 .
. . . . . . . . . 2 2 2 . . 9 9 . . . 9 . . 1 1 1 3 9 . . 9
9 9 . . 3 . . . . . . 9 2 2 2 9 9 9 9 9 . 4 4 . 1 3 . . . .
. 9 9 . 3 . . . 9 9 9 9 9 9 . 9 9 9 9 1 1 1 4 1 9 9 . 9 9 .
. 9 9 . . . . 9 9 9 9 9 9 9 9 9 9 9 9 6 6 6 3 2 7 7 7 . . .
Figure 10.12
Statistique d'oscillation pour un réseau booléen aléatoire dans le régime chaotique (p = 0,28). On observe la percolation de l'ensemble des nœuds oscillants.10-3-6 L'"aimantation"
L'aimantation d'un nœud, ainsi nommée par référence à la physique des milieux magnétiques, est la moyenne temporelle de l'état du nœud. Elle est évaluée après la période transitoire. Si l'état du nœud est fixe, l'aimantation vaut 0 ou 1. Pour les courtes périodes locales, l'aimantation prend des valeurs fractionnaires: 1/4, 1/3, l/2, 2/3... Par conséquent, dans le régime organisé, l'histogramme des aimantations observées sur l'ensemble du réseau est une succession de pics discrets (Fig. 10.13). Par contre, dans le régime chaotique, cet histogramme est continu (Fig. 10.14). Cette différence de comportement est à rapprocher des spectres de fréquence des systèmes différentiels non linéaires: les régimes périodiques sont caractérisés par des spectres discrets, tandis que les régimes turbulents font apparaître des spectres continus.

Figure 10.13 Histogramme des aimantations dans le régime organisé (p = 0,2). (D'après B. Derrida, "Phase Transitions in Random Networks of Automata", in Chance and Matter, eds. J. Souletie, J. Vannimenus et R. Stora, Les Houches 1986, North Holland 1987).

Figure 10.14 Histogramme des aimantations dans le régime chaotique (p = 0,3). "Phase Transitions in Random Networks of Automata", in Chance and Matter, ibid.).
10-4 LA METHODE DES DISTANCES
Cette méthode s'est avérée récemment comme l'une des plus fécondes pour déterminer la dynamique d'un réseau. Rappelons que la distance de Hamming entre deux configurations est le nombre des automates dans un état différent. Cette distance est nulle si les deux configurations sont identiques, et égale au nombre des automates si les deux configurations sont complémentaires. On obtient la distance relative en divisant la distance de Hamming par le nombre des automates.
Le principe de la méthode des distances est le suivant: on choisit deux conditions initiales séparées par une certaine distance, et l'on suit l'évolution de cette distance au cours du temps. La quantité étudiée est le plus souvent la moyenne de la distance asymptotique, mesurée dans la limite des grands temps. On prend cette moyenne sur un grand nombre de réseaux et de conditions initiales, pour une distance de départ fixée. Suivant la distance initiale, on peut envisager que les deux configurations évoluent vers le même point fixe (auquel cas la distance tend vers 0), vers deux attracteurs différents, ou même restent à distance finie (dans le cas d'un seul attracteur périodique), que la période soit grande ou relativement petite. On observe encore une fois une différence de comportement entre les deux régimes. Sur la figure 10.15, l'abscisse est la moyenne des distances relatives entre les configurations initiales, et l'ordonnée, la moyenne des distances relatives aux grands temps. Dans le régime chaotique, on observe que si la distance initiale est différente de 0, la distance finale est supérieure à 10%. La distance finale semble pratiquement indépendante de la distance initiale. Par contre dans le régime organisé, la distance finale est proportionnelle à la distance initiale.
On peut en fait considérer deux configurations voisines comme l'ensemble formé d'une configuration de référence et d'une configuration perturbée en quelques sites. Le résultat obtenu pour le régime organisé s'interprète facilement en tenant compte des sous-réseaux indépendants: la distance finale est proportionnelle au nombre de sous-réseaux perturbés, et ce nombre est lui-même proportionnel au nombre des automates initialement modifiés. Dans le cas du régime chaotique, non structuré, la perturbation se transmet à travers tout le réseau. On observe donc l'équivalent de la sensibilité aux conditions initiales, caractéristique des régimes chaotiques dans les systèmes continus.

Figure 10.15 Distances relatives aux grands temps en fonction des distances relatives initiales, dans le régime organisé (p = 0,2), et dans le régime chaotique (p = 0,3). (D'après B. Derrida et D. Stauffer, Europhys. Lett. 2, p. 739, 1986.)
Les réseaux dilués
Il est possible de prédire l'évolution des distances dans le cas des réseaux dilués, c'est-à-dire à connectivité aléatoire et tels que le rapport k/N soit proche de 0.
Considérons tout d'abord deux configurations prises au hasard dans le cas d'un réseau quelconque de connectivité k. Evaluons l'évolution en une étape de l'itération du recouvrement x(t). Le recouvrement est le rapport entre le nombre des automates dans le même état, et N. Autrement dit:
x = 1 - d (10.6)
où d est la distance relative. C'est aussi la probabilité que deux automates soient dans le même état. A l'instant initial, N x(t) automates sont dans le même état. Par conséquent, tous les automates dont les k automates d'entrée sont dans ce sous-ensemble resteront dans le même état à l'instant t+1, après l'itération. Leur nombre est N x(t)k. En l'absence de corrélations entre les états et les automates, tous les autres automates ont une chance sur deux de se retrouver dans le même état. Par conséquent:
![]()
![]()
Cette expression n'est valable que pour deux configurations aléatoires. Elle ne peut donc pas en principe être itérée pour déterminer x aux grands temps, car les configurations atteintes au cours de l'itération ne sont plus aléatoires. En particulier, les états des entrées d'un nœud donné peuvent être corrélés par l'existence d'ancêtres communs. L'itération de l'expression (10.7) est néanmoins possible:
• Pour les réseaux dilués, pour un nombre limité d'étapes de telle sorte que les ancêtres communs des entrées d'un même nœud soient rares. Cela est vrai tant que le nombre d'itérations est plus petit que logN/logk.
• Pour les réseaux recuits. Un réseau recuit est un réseau dont les fonctions des automates sont tirées au sort à chaque itération, ce qui détruit les corrélations entre les configurations et les automates. Ces réseaux ont été proposés par B. Derrida et Y. Pomeau.
Si l'on effectue l'itération de l'expression (10.7), on observe deux comportements possibles, suivant que la courbe x(t+1) fonction de x(t) croise ou non la première bissectrice pour x compris entre 0 et 1. Pour les petites connectivités, jusqu'à 2, il n'y a pas d'intersection entre 0 et 1 et le recouvrement tend vers 1 aux grands temps. C'est ce qu'on observe sur la figure 10.16. Par contre si k > 2, la première bissectrice coupe la diagonale avant que x = 1, et le recouvrement aux grands temps reste inférieur à 1.
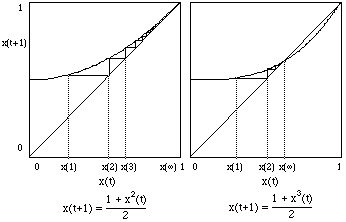
![]()
Figure 10.16
Itération du recouvrement relatif pour des connectivités de 2 (à gauche) et de 3 (à droite).Dans le premier cas de figure, la distance entre les deux configurations initiales tend vers 0, ce qui veut dire que le nombre des configurations accessibles au système tend vers 0 aux grands temps. Il s'agit bien là d'un comportement organisé.
Dans le deuxième cas de figure, la distance reste finie: l'espace accessible au système est de l'ordre de 21-x. La distance aux grands temps semble indépendante de la distance initiale: il s'agit bien là d'un comportement chaotique.

Figure 10.17. Evolution des recouvrements x(t). Comparaisons entre réseaux "gelés" à gauche et réseaux "recuits" à droite. Les figures du haut sont obtenues pour des connectivités k = 2, et celles du bas pour des connectivités k = 3. Les courbes en traits pleins sont obtenues en itérant la formule 10.7, et les points sont des résultats de simulations numériques (les + correspondent à des réseaux de 32 automates, les • à 256, les x à 2 048 et les o à 16 384). (D'après B. Derrida et G. Weisbuch, J. Physique, 47, p. 1297, 1986.)
Nous avons comparé les prédictions théoriques de la formule 10.7 avec des simulations numériques faites sur des réseaux recuits et des réseaux "gelés", c'est-à-dire dont les fonctions des automates sont fixes. On peut observer que les deux types de réseaux ont un comportement identique au début des itérations. La transition de phase prédite par l'équation 10.7 pour les réseaux recuits correspond donc à celle observée pour les réseaux gelés. Les différences notables de comportement s'observent essentiellement aux grands temps pour les réseaux organisés (k = 2): le recouvrement tend vers des valeurs finies inférieures à 1 pour les réseaux gelés. Mais la différence entre cette valeur limite et 1 tend vers 0 lorsque la taille du réseau augmente (Fig. 10.17).
10-5 Conclusions
Toute cette étude fait clairement apparaître les deux types de comportement, organisé et chaotique. Le tableau 10.1 résume les différences de propriétés génériques suivant les deux régimes.

Tableau 10.1
Propriétés génériques des réseaux aléatoires.La méthode des distances a été utilisée dans un grand nombre de cas pour étudier les comportements dynamiques de différents réseaux, à connectivité cellulaire ou aléatoire, pour des automates à seuil ou des automates booléens, pour des automates probabilistes ou déterministes. Dans le cas des systèmes dilués aléatoires, elle permet des prédictions théoriques, comme celle de la transition de régime des réseaux booléens ou la capacité des réseaux dilués d'automates à seuil (voir le paragraphe 6.3). Dans le cas de la connectivité cellulaire, les prédictions théoriques sont impossibles, mais les comportements sont qualitativement semblables à ceux des réseaux dilués; de plus, la technique est simple à mettre en œuvre dans les simulations numériques, et elle permet une détermination relativement efficace des paramètres de la transition. Les figures qui suivent en montrent l'application aux verres de spins à interactions entre plus proches voisins (modèle d'Ising, voir le paragraphe 8.5).
10-6 APPLICATION DE LA METHODE DES DISTANCES AUX VERRES DE SPINS
Le réseau est défini par les constantes d'interactions entre spins voisins: les Tij valent +1 ou -1 et sont tirés au sort. Les deux configurations dont on étudie la distance sont soumises à une itération parallèle. De plus, pour tenir compte de la température, la dynamique est probabiliste, mais les deux configurations sont soumises au même bruit thermique. Plus précisement, pour choisir l'état +1 pour le spin i avec une certaine probabilité p donnée par la formule (8.8), on compare p à un nombre z tiré au sort entre 0 et 1. Si p est inférieur à z, ce qui se produit avec une probabilité p, le spin prend la valeur +1; sinon il prend la valeur -1. On réalise le même bruit thermique en utilisant le même nombre z pour les deux configurations.
Il est tout d'abord intéressant de rechercher l'organisation spatiale d'un verre de spins comme nous l'avons fait pour les réseaux d'automates booléens. On a donc suivi l'évolution d'un réseau à deux dimensions de taille 1005100 spins, à une température de 0,9. La partie gauche de la figure 10.18 représente la valeur absolue de l'aimantation moyenne après 1 250 itérations pour une des configurations A. Les régions blanches correspondent à des aimantations nulles en moyenne: les spins y oscillent donc perpétuellement. Dans les régions noires, les spins ont une aimantation d'amplitude 1: ils sont donc fixes.
La figure de droite met en évidence des structures plus grandes. Elle représente la distance entre deux configurations A et B qui ont évolué parallèlement sous l'influence du même bruit thermique. Dans les régions noires les spins sont identiques, dans les régions blanches ils sont opposés. Les configurations attractrices sont donc divisées en domaines relativement indépendants susceptibles d'inverser leur polarisation. Bien entendu, si l'on observe directement chacune des configurations aucune structure à grande échelle n'est visible; aucune corrélation entre les états de deux spins voisins n'apparaît à cause du désordre.

Figure 10.18
On peut aussi moyenner la distance entre les deux configurations sur tout l'échantillon. La figure 10.19 montre l'évolution de la distance aux grands temps (t = 500) en fonction de la température pour des échantillons cubiques de 12512512 spins. Trois comportements différents peuvent être observés:
• A haute température, T > 4, dans la phase paramagnétique, il n'y a qu'un seul attracteur et la distance entre les deux configurations est nulle.
• A basse température, T < 1,8 , dans la phase verre de spins, la multiplicité des attracteurs est telle que chaque configuration est piégée dans un attracteur voisin de la configuration initiale: la distance finale entre les configurations dépend donc de la distance initiale.
• Entre les deux la distance finale est toujours finie et indépendante de la distance initiale. Les attracteurs sont structurés en grands domaines qui ne fluctuent guère tant que la température n'est pas trop élevée. Chaque configuration évolue vers l'un de ces attracteurs, et la distance observée correspond à la distance moyenne entre ces attracteurs.
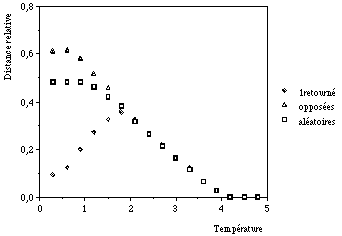
Figure 10.19
Distances relatives entre deux configurations du même verre de spins, après 500 itérations, en fonction de la température. Le réseau à trois dimensions contient 12512512 spins. (Les résultats on été moyennés sur 200 échantillons.) Les triangles correspondent à deux configurations initialement opposées, les carrés à deux configurations aléatoires et les losanges à deux configurations ne différant initialement que par un seul spin. Aux températures supérieures à 2, les points représentatifs des trois distances initiales sont pratiquement confondus. (D'après B. Derrida et G. Weisbuch, Europhysics Let., 4, p. 657, 1987).Références
On pourra lire au sujet de la transition: "Dynamical Phase Transitions in Random Networks of Automata", par B.Derrida, in Chance and Matter édité par J. Souletie, J. Vannimenus et R. Stora, North Holland (1987).
Pour la notion de percolation voir: Introduction to Percolation Theory, de D. Stauffer, publié par Taylor and Francis (1985), et pour le chaos, L'ordre dans le chaos de P. Bergé, Y Pomeau et C. Vidal, Hermann (1984).