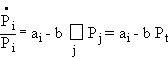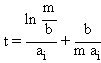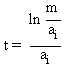CHAPITRE 11
Génotypes et phénotypes
Quels sont les principes
de l'organisation fonctionnelle des systèmes vivants à partir du message
génétique porté par le génome?
Ce problème est souvent
minimisé par la biologie moléculaire classique: dans ce cadre, à partir du
moment où toute l'information est codée dans le génome, le développement de
l'organisme est "programmé" d'une manière univoque. Il en va de même
pour l'évolution des espèces, soumises à une pression de sélection: seules les
plus "adaptées" survivent. Toujours dans cette optique, l'objet de la
biologie en tant que science est de décrire les mécanismes spécifiques de
chacune des interactions permettant d'établir à chaque niveau le comportement
du système considéré: il pourra s'agir aussi bien de conformation de
macromolécules, que de métabolisme cellulaire, de développement ontogénétique
ou phylogénétique.
Dans ce chapitre, nous
entreprendrons à l'inverse de décrire l'émergence des propriétés collectives
d'organisation indépendamment du détail des interactions entre les composants.
Autrement dit, nous sommes à la recherche de comportements génériques, au sens
défini au chapitre précédent.
Le génome, ou génotype,
est le message génétique contenu dans l'ADN des chromosomes. C'est le génome
qui détermine, en partie en fonction des conditions extérieures, le phénotype
de l'organisme, c'est-à-dire l'ensemble de ses propriétés physico-chimiques et
ses fonctions biologiques: arrangement et fonctionnement des organes, taille,
poids, sexe... Mais ce déterminisme admis par tous les scientifiques est loin
d'être compris à tous les niveaux. Ce qui est clair aujourd'hui, c'est le code
génétique, c'est-à-dire la correspondance entre les bases des acides nucléiques
(leurs composants élémentaires) et les acides aminés qui composent les
protéines. Mais, dès que l'on dépasse ce premier niveau, surgissent les
mystères: comment la séquence des acides aminés détermine-t-elle la
configuration spatiale des protéines, responsable de leur réactivité chimique?
comment les protéines interagissent-elles pour déterminer la structure
cellulaire? etc. La série des questions continue jusqu'au niveau de la
constitution des organes, de l'organisme et des interactions entre populations.
Dans ce chapitre nous allons aborder la
question de la relation génotype/phénotype par une approche réseau d'automates,
en nous préoccupant de propriétés très générales des êtres vivants. Nous
traiterons trois exemples: la différenciation cellulaire, l'origine de la vie
et l'évolution des espèces.
11-1 LA DIFFERENCIATION CELLULAIRE
Le paradoxe apparent de la différenciation
cellulaire est le suivant:
"Puisque
l'information génétique contenue dans chaque cellule est la même, comment se
fait-il qu'il existe au sein d'un même organisme pluricellulaire des cellules
de type différent?"
En effet, notre corps
contient des cellules de morphologies et de fonctions biologiques différentes:
neurones, cellules du foie, globules rouges... en tout plus de 200 types
cellulaires différents. Or les chromosomes porteurs de l'information génétique
ne diffèrent pas d'une cellule à l'autre. Une partie de la réponse est que
toutes les protéines codées par le génome ne sont pas exprimées (c'est-à-dire
effectivement synthétisées avec une concentration non nulle) dans une cellule
d'un type déterminé. L'hémoglobine n'est présente que dans les globules rouges,
les neurotransmetteurs et leurs récepteurs n'apparaissent que dans les neurones,
etc.
Plusieurs mécanismes
peuvent interférer avec les différentes étapes de l'expression d'un gène et la
faciliter ou au contraire l'empêcher. On parle alors d'activation ou de
répression. Les mécanismes les mieux connus concernent les premières étapes de
la transcription. Pour que l'ADN puisse être transcrit, une protéine
spécifique, la DNA polymérase, doit pouvoir se fixer sur un site précédant sur
la chaîne la partie codée de la macromolécule, le promoteur. Or ce promoteur
peut être partiellement recouvert par une protéine de contrôle, dite
répresseur; la lecture de la suite de la chaîne est alors impossible. Suivant
que le répresseur est présent en quantité ou non, le gène est donc non exprimé
ou exprimé. La protéine jouant le rôle de répresseur est elle aussi codée par
un autre gène, lui-même soumis à un contrôle par une ou plusieurs autres
protéines. Il est donc tentant de modéliser le réseau de ces interactions
enchevêtrées par un réseau d'automates.
• Un gène est alors représenté par un automate dont l'état binaire
indique s'il est effectivement exprimé. Si le gène est dans l'état 1, il est
exprimé et la protéine est présente en concentration importante dans la
cellule. Celle-ci est donc susceptible de contrôler l'expression d'autres
gènes.
• L' action des protéines de contrôle sur ce gène est représentée
par une fonction booléenne, dont les entrées sont les gènes codant les
protéines contrôlant son expression.
• Le génome lui-même est représenté par un réseau d'automates
booléens représentant les gènes en interaction.
Dans un tel réseau, les
seules configurations subsistant au bout de quelques cycles d'itération sont
les attracteurs de la dynamique, points fixes ou cycles limites, tout au moins
lorsque la dynamique n'est pas chaotique. Ces configurations s'interprètent en
termes de types cellulaires: en effet, une configuration correspond à la
présence de certaines protéines, et donc à la fonction biologique de la cellule
et à sa morphologie. Par conséquent, Si nous connaissions l'ensemble des
mécanismes de contrôle de chacun des gènes d'un organisme, nous pourrions en
prédire les types cellulaires. En fait, cela n'est jamais le cas, même pour les
organismes les plus simples. Nous ne connaissons en fait les mécanismes de
contrôle que dans le cas de quelques gènes. L'ensemble des mécanismes
conduisant à la consommation du lactose chez Escherichia coli, dit
opéron lactose, a été décrit par Monod et al. Dans l'ignorance d'un
schéma complet des interactions, S. Kauffman (1969) s'est proposé de mettre en
évidence les propriétés génériques de l'ensemble des génomes en les
représentant par des réseaux booléens
aléatoires. En effet, les lois booléennes possibles pour un automate de
connectivité d'entrée donnée k étant en nombre fini, il est possible de construire
par tirage au sort un réseau aléatoire de connectivité donnée.
Comme nous l'avons déjà dit au chapitre
précédent, Kauffman a donc déterminé par simulation numérique les lois
d'échelle reliant la période moyenne des cycles limites et le nombre de cycles
limites différents, à N, le nombre des automates du réseau. Pour la
connectivité 2, ces deux grandeurs semblent varier comme la racine carrée de N
(en fait les fluctuations sont très importantes). Or ces lois d'échelle sont
aussi celles observées pour le temps entre divisions cellulaires et pour le
nombre de types cellulaires en fonction du nombre de gènes par cellule (Fig.
11.1). Le nombre de types cellulaires différents correspond bien dans le modèle
de Kauffman au nombre des attracteurs. Quant au temps de division cellulaire,
il est normal de le comparer à la grandeur temporelle liée aux attracteurs de
la dynamique, c'est-à-dire la période.
Il est clair que les approximations
de Kauffman sont extrêmement grossières comparées à la réalité biologique:
variables binaires représentant les
concentrations des protéines, fonctions booléennes (donc discrètes),
simultanéité des transitions des automates, structures aléatoires..... La
robustesse des résultats obtenus par rapport aux modifications possibles du
modèle (il s'agit de réseaux aléatoires) justifie cette approche. L'existence
d'un grand nombre d'attracteurs, quant à elle, n'est certainement pas liée aux
spécifications particulières des réseaux choisis: c'est une propriété générique
des systèmes complexes, qui apparaît dès qu'il existe des frustrations dans le
réseau des interactions entre les éléments.
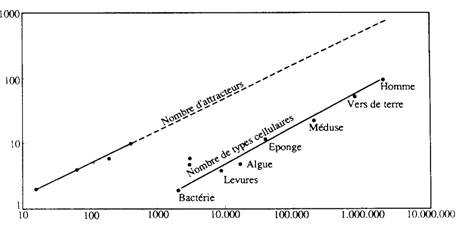
Figure 11.1
Variation du nombre de types cellulaires en fonction du nombre de gènes par
cellule. On a représenté ici les deux lois d'échelle, celle du modèle de
Kauffman, nombre de cycles limites différents en fonction du nombre des
automates, et celle des organismes biologiques. Les deux échelles sont
logarithmiques. Les deux courbes sont à peu près parallèles et correspondent à
une pente de 0,5. (D'après S. Kauffmann, "Binary Elements Nets" in
Towards a Theoretical Biology 3. Drafts, ed. C. Waddington,
Edinburgh University Press, 1970).
11-2 L'ORIGINE DE LA VIE
Les problèmes de
l'origine de la vie sur Terre se posent de manière différente suivant le niveau
d'organisation auquel on s'intéresse. Historiquement, le problème s'est d'abord
posé en termes de chimie: comment expliquer l'apparition de molécules
organiques, dans un milieu oxydant dans lequel ces composés auraient plutôt
tendance à brûler en libérant de l'énergie? Puis on s'est intéressé aux groupes
fonctionnels plus spécifiquement liés au vivant comme les acides aminés et les nucléotides.
Toute une série d'expériences ont démarré dans les années cinquante, rappelant
un peu les motivations et la méthode de l'oeuf de Berthelot. On mélange en
général dans une ampoule des constituants inorganiques élémentaires, eau, air,
gaz carbonique.. et l'on observe la présence de composés
"intéressants" de type acides aminés et nucléotides, après une
décharge électrique dans le milieu (Orgel).
En fait le problème
conceptuel le plus délicat se situe au niveau biochimique et concerne la
réplication des acides nucléiques et la synthèse des protéines. En effet, ces
deux opérations requièrent la présence de protéines jouant le rôle de
catalyseurs spécifiques. Avant l' "apparition" des protéines, la
synthèse des protéines, comme celle des acides nucléiques, est donc impossible, alors que ces derniers sont
nécessaires à cette même synthèse. C'est en somme la version biochimique du
problème de l'œuf et de la poule. La réponse en termes de physique consiste
évidemment à évoquer un mécanisme d'instabilité.
Suivant une terminologie
à la Prigogine, il est tout d'abord nécessaire d'imaginer des mécanismes
autocatalytiques au cours desquels le produit d'une réaction est utilisé dans
une partie des réactions qui interviennent dans sa synthèse. Dans ce cadre, le
premier modèle de l'apparition des "hypercycles" autocatalytiques
entre protéines et acides nucléiques a été proposé par M. Eigen (1971). Il est
basé sur un sytème non linéaire d'équations différentielles du premier ordre
dont les variables sont les concentrations chimiques (Ci) des espèces (i, j, k..) en solution.
Une de ces équations cinétiques s'écrit par exemple:
dCi/dt = (ai +
bij Cj )
Ci + cik Ck (11.1)
où le terme en bij Cj Ci représente la synthèse de l'espèce chimique i
catalysée par l'espèce j. Les bij
étant positifs, ces systèmes différentiels non linéaires ont des modes
instables, et celui dont la croissance est la plus rapide l'emporte sur les
autres. Il y a alors "émergence" d'un ensemble de composés et d'un
métabolisme de reproduction entre ces espèces sélectionnées.
La dynamique proposée par Eigen est assez
simpliste dans la mesure où elle est entièrement déterministe (pas d'erreur
dans la duplication de l'ADN) et où elle suppose tous les composés susceptibles
d'interagir présents dans la solution en concentration finie. Elle ne peut
conduire qu'à un seul hypercycle, le plus instable, ce qui contredit quelque
peu la diversité d'organismes que l'on
observe. En revanche elle assure la stabilité de cet hypercycle.
C'est pour tenter de reproduire à la fois les
propriétés de stabilité et de diversité observées dans le monde vivant que P.
Anderson a proposé un modèle basé sur une analogie avec les propriétés des
verres de spins. Le modèle est construit au niveau des molécules individuelles,
et non pas au niveau de leurs concentrations, ce qui rend les simulations
numériques plus longues et plus difficiles.
On considère au départ
une "soupe" composée de monomères, de quelques oligomères, petites
chaînes de quelques monomères, et des molécules porteuses d'énergie
susceptibles de permettre les réactions biochimiques. On simplifie le problème
de biochimie en supposant que les protéines n'étaient pas au début indispensables au maintien de cycles
autocatalytiques entre les polynucléotides. On peut sans dommage continuer à
simplifier en supposant que les bases azotées ne sont qu'au nombre de 2, par
exemple A et T, représentées par des spins +1 et -1. La séquence des bases d'un
polynucléotide est donc représentée par une chaîne linéaire de spins +1 et -1.
Les polynucléotides
existent en solution sous forme de chaînes linéaires en simple brin, ou sous
forme de double hélice à deux brins, associés par les paires de base
complémentaires + - ou - + reliées entre elles par des liaisons hydrogènes très
labiles. La transition entre les deux formes est réversible. Les basses
températures et les fortes concentrations favorisent la forme en double hélice,
alors que les hautes températures et les faibles concentrations favorisent la
rupture de celle-ci et les formes en simple brin.
On est amené à considérer
deux types de réactions chimiques.
• La première séquence de réactions concerne la
synthèse des polynucléotides. Cette synthèse fait intervenir une chaîne
de trois réactions dont les deux extrêmes sont inverses l'une de l'autre et
supposent des variations cycliques de l'environnement. Elle aboutit à la
concaténation sur "gabarit", de bouts de chaîne partiellement
complémentaires du gabarit, en trois étapes :
Première étape: formation
d'une double hélice par suite du changement des conditions physiques
(refroidissement par exemple). Cette double hélice est constituée à partir d'un
brin qui sert de gabarit et de deux autres, partiellement complémentaires du
gabarit, qui viennent se fixer sur lui par des liaisons hydrogène entre bases
complémentaires:
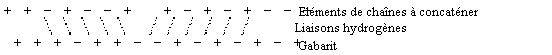
Deuxième étape: formation
d'une liaison covalente entre les deux extrémités des bouts condensés sur le
gabarit.
Troisième étape: sous
l'effet d'un réchauffement par exemple, les deux brins se séparent à nouveau,
et sont alors disponibles pour intervenir dans un nouveau cycle, soit comme
gabarits soit comme réactifs. Ce type de réaction inclut la reproduction avec
possibilité de mutation dans la mesure où il n'est pas nécessaire que la
complémentarité des chaînes soit parfaite pour qu'il y ait formation d'une
double hélice. Bien entendu, la fixation d'un monomère en bout de chaîne n'est
qu'un cas particulier de ce mécanisme. L'hypothèse de base sur l'alternance de
périodes chaudes et froides peut très bien s'expliquer par des cycles d'ombre
et de lumière ou des cycles journaliers. Cette série de réactions a déjà été
proposée et étudiée par les biochimistes (Blum 1962, Kuhn 1978...), et l'apport
des physiciens théoriciens concerne les réactions de dissociation.
• Les réactions de dissociation d'une
chaîne.
Dans un environnement
chimique déterminé, il existe toujours des réactions d'hydrolyse d'une chaîne
conduisant à sa dissociation. Dans un modèle de cinétique chimique comme celui
de M. Eigen par exemple, ceci se traduit par un terme en ai Ci
avec ai négatif. Dans une
simulation numérique comme celle de P. Anderson, D. Stein et D. Rokhsar, on
fait intervenir un tirage au sort avec une probabilité de dissociation.
Celle-ci dépend de nombreux facteurs, comme la solidité des liaisons
covalentes. Si les liaisons entre bases voisines étaient indépendantes les unes
des autres, la probabilité de dissociation de la chaîne ferait intervenir un
produit de probabilités de dissociation de chaque liaison; le problème pourrait
alors se réduire à un problème de mécanique statistique entre particules
indépendantes. Mais l'accessibilité des liaisons dépend de la structure
secondaire (les liaisons hydrogène entre
les bases de la même chaîne), de même que de la structure tridimensionnelle de
celle-ci. Il s'agit donc d'une propriété collective de l'ensemble des
bases de la chaîne. D'où l'idée de calculer cette probabilité à partir d'une
expression semblable à celle de l'énergie dans un verre de spins. La fonction
de dissociation d'une chaîne est donnée par:
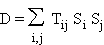
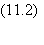
où les indices i et j se
réfèrent cette fois aux monomères.
La probabilité de
dissociation intervenant dans les simulations numériques est une fonction de
Fermi-Dirac de la fonction de décès:
P = \F(1;1 + exp [-D-m(N)]) (11.3)
où m(N), le potentiel
chimique, maintient la longueur des polymères autour d'une certaine moyenne.
Dans l'ignorance où nous
sommes des Tij intervenant
dans la physico-chimie des polynucléotides, on choisit pour ceux-ci une
distribution aléatoire, par exemple suivant le modèle de
Sherrington-Kirkpatrick.
Bien entendu, les espèces
chimiques dont la fonction de dissociation est minimum sont privilégiées. Le
mécanisme de reproduction par complémentarité décrit plus haut, plus la
sélection naturelle assurée par la fonction dissociation, assurent la stabilité
d'un certain nombre d'espèces chimiques. La diversité de ces espèces est
assurée par l'existence d'un grand nombre de minima secondaires des fonctions
de dissociation.
Les simulations
numériques démarrent à partir d'une soupe originelle où ne sont présents que
des monomères, et l'ensemble de tous les trimères en concentration équivalente,
de manière à ne pas favoriser a priori la croissance de telle ou telle
séquence. Elles font alterner les phases de concaténation sur gabarit par
recherche des morceaux de chaînes susceptibles de s'associer par
complémentarité sur celui-ci, et les phases de destruction des chaînes par
tirage au sort et comparaison à la probabilité de destruction de la chaîne.
La figure 11.2, par
exemple, montre la disparition de certaines espèces et la prédominance d'autres
au cours du temps.
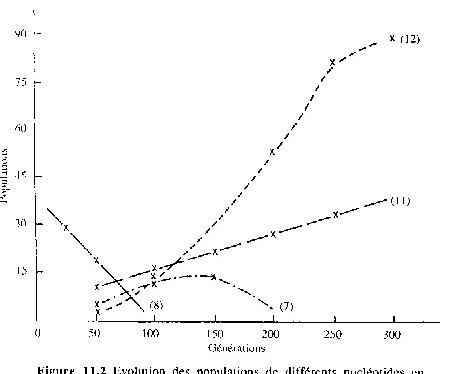
Figure 11.2 Evolution des populations de différents nucléotides
en interaction dans une soupe originelle. On voit que deux des quatre espèces
suivies sont sélectionnées alors que les deux autres disparaissent. (D'après D.
Rokhsar, D. Stein et P. Anderson, J. Mol. Evol., 23, p. 119 1986.)
La figure 11.3 montre l'effet d'un changement
de l'environnement modélisé par une modification des Tij. L'espèce A disparaît, l'espèce B
envahit l'espace, l'espèce C après quelques difficultés initiales s'adapte
après mutation.
Les nombreuses
simulations du groupe de Princeton font ressortir le caractère générique des
résulats obtenus. Pour une très large gamme de paramètres d'interaction et de
potentiels chimiques, on retrouve qualitativement les mêmes résultats:
sélection d'un petit nombre d'espèces correspondant aux vallées de la fonction
D, et stabilité ultérieure des espèces sélectionnées. D'où l'idée que les
comportements observés sont indépendants des détails du modèle. En particulier,
si au lieu d'une fonction de type verre de spins on était en mesure d'utiliser
les données expérimentales de la biochimie, on observerait qualitativement les mêmes
comportements.
Figure 11.3
Evolution de trois populations de polynucléotides lors d'un changement de
l'environnement. L'espèce A n'est plus adaptée et disparaît. L'espèce B
bénéficie du changement. L'espèce C s'adapte après une mutation.( D'après D.
Rokhsar, D. Stein et P. Anderson, J. Mol. Evol., ibid.)
11-3 L'EVOLUTION DES ESPECES
L'évolution des espèces
est un processus dynamique à trois niveaux: génotype, phénotype et populations.
Comme pour l'origine de la vie, cette dynamique est encore compliquée par la
boucle de rétroaction entre le niveau supérieur, celui des populations, et le
niveau inférieur, celui du génome (Fig. 11.4).

Figure 11.4 La boucle des interactions entre les trois niveaux
intervenant dans l'évolution des espèces.
Est-il possible de
caractériser les propriétés génériques de la dynamique malgré notre ignorance
des mécanismes du développement (le passage du génotype au phénotype) et de la
sélection "naturelle" (le passage des phénotypes aux populations) ?
L'actualité de cette question est en partie liée à un débat sur les
"équilibres ponctués" lancé par deux paléontologistes S. Gould et N.
Eldredge.
Il existe quelques
résultats semi-quantitatifs permettant de suivre la dynamique de l'évolution.
Ces résultats semblent malheureusement contradictoires suivant que l'on étudie
les génomes ou les propriétés phénotypiques. Les études sur les génomes sont
faites en comparant les protéines homologues (c'est-à-dire ayant la même
fonction biologique), entre les différentes espèces vivantes (Zuckerkandl). On
en déduit que le taux des mutations, mesuré par les différences entre séquences
d'acides aminés, est resté constant tout au long de l'histoire de la Terre. Par
contre, si l'on mesure certaines grandeurs phénotypiques comme la taille des
espèces, on observe parfois des équilibres ponctués: de longues stases,
durant lesquelles l'évolution semble arrêtée, sont séparées par de brèves
périodes d'évolution très rapide, pratiquement des discontinuités apparentes
(il faut penser à la difficulté de trouver des fossiles).
Or, les modèles
mathématiques standard de l'évolution, de type génétique des populations, sont
basés sur une hypothèse "mendéléenne" extrême, la correspondance un
gène/un caractère. Autrement dit, chaque caractère phénotypique est déterminé
par un seul gène. Dans ce cadre, un taux de mutation constant au niveau des
gènes ne peut entraîner, au niveau phénotypique, de sauts brusques comparables
à ceux des équilibres ponctués. Pour résoudre ce paradoxe, les paléontologistes
ont recours à deux types d'explications:
• des événements isolés, de type "catastrophes"
climatiques, géologiques ou météorites, qui peuvent avoir soudain changé les
conditions de la vie sur Terre;
• la possibilité que les mutations responsables des changements
d'espèces soient de type différent de celles qui sont observées à l'intérieur
d'une même espèce, et qui sont correctement décrites par la génétique des
populations standard.
Nous allons voir, en
fait, que si l'on prend en compte le fait que le phénotype est une propriété
d'ensemble du génome, et non pas une collection de caractères indépendants
déterminé chacun par un seul gène, aucune hypothèse supplémentaire du type de
celles proposées par les paléontologistes n'est nécessaire pour expliquer les
équilibres ponctués.
11-3-1 Dynamique des populations
Le rôle de la robustesse
Supposons que tous les organismes possibles
aient un génome comprenant N gènes et que chaque gène puisse apparaître sous
quatre formes différentes, les allèles. Il existe alors 4N organismes possibles. Soit Pi la population de l'organisme i. Pour
caractériser l'évolution, il faut décrire au cours du temps les variations des
populations dans l'espace à 4Ndimensions
de tous les génomes. En chaque site de cet espace, une population évolue sous
l'influence des naissances, des décès, de la compétition entre les organismes;
sous l'effet des mutations, des organismes sautent parfois d'un site à l'autre.
On peut imaginer un système d'équations
différentielles auquel obéissent les populations, comprenant des termes de
reproduction, de décès, etc. Une fois
connus tous ces termes, il suffirait de résoudre les équations, ou au moins de
caractériser la dynamique à partir de simplifications raisonnables.
La difficulté essentielle de ce programme est
la prise en compte du lien entre le génome des organismes i et les termes
intervenant dans les équations. Pour ce faire, il faudrait avoir compris les
mécanismes du développement et nous en sommes toujours très loin. Nous allons
passer outre cette difficulté en traduisant le fait que le phénotype fait
intervenir les propriétés collectives du
génotype. Supposons que le génome soit modélisé par un réseau de Kauffman de
faible connectivité. Les caractères phénotypiques dépendent alors des
attracteurs de la dynamique du réseau. Or les propriétés dynamiques globales de
ces réseaux se caractérisent par une très grande robustesse. La
robustesse traduit le fait que le changement d'une faible fraction des
automates d'un réseau n'a que peu d'effet sur ses attracteurs. Nous n'avons
jusqu'ici discuté de la stabilité des attracteurs que par rapport à de petites
perturbations des configurations initiales. Mais il est clair que la stabilité
par rapport aux conditions initiales entraîne la robustesse par rapport aux
petites perturbations du réseau. Les motifs en sont les mêmes: structures
forçantes et structuration en sous-réseaux indépendants. Les simulations numériques
permettent d'ailleurs de vérifier la robustesse des réseaux booléens
aléatoires. La même robustesse s'observe aussi pour les réseaux de Hopfield ou
assimilés: la défaillance éventuelle d'un seul des automates ne modifie pas
l'état des autres automates sur une configuration attractrice lorsque le terme
de signal est important. La robustesse traduit le fait que deux génomes ne
différant que par quelques automates, donc voisins dans l'espace des génomes,
ont des propriétés dynamiques voisines.
Les équations de départ
Nous partons du système
d'équations différentielles 11.4 décrivant l'évolution des populations Pi en chaque point de l'espace des
génomes:
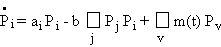
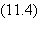
Les indices i, j et v se
rapportent aux organismes. i est spécifique de l'organisme considéré, j peut
être n'importe quel organisme, v représente les organismes qui ne différent de
i que par un seul gène.
La dérivée par rapport au
temps de la population des organismes est donc la somme de trois termes.
• Le premier terme est un terme de croissance qui prend en compte le
bilan entre la reproduction, les décès des individus et les mutations vers les
génomes voisins. Le coefficient de proportionnalité ai est appelé adaptabilité de
l'organisme i.
• Le second terme représente sous forme différentielle le partage
des ressources, nourriture par exemple, entre tous les organismes; c'est la
raison de la somme sur j.
• Le troisième terme représente l'accroissement de population dû aux
mutations en provenance des organismes
de génome voisin. L'amplitude de ce terme est proportionnelle à m(t) qui
fluctue au cours du temps autour d'un taux moyen m, petit par rapport aux coefficients
d'adaptabilité.
Il s'agit bien sûr
d'un modèle très simplifié qui ne tient
pas compte de la reproduction sexuée, qui n'admet que des mutations
ponctuelles, et pour lequel la compétition entre organismes se limite au
partage d'une seule ressource.
En fait, la base du
modèle est que les adaptabilités ai
peuvent être choisies comme proportionnelles à l'une quelconque des propriétés
dynamiques du réseau i, comme par exemple la plus grande période des
attracteurs, la période moyenne, le nombre des attracteurs, etc. Autrement dit,
le paysage des adaptabilités dans l'espace des
génomes a l'aspect de la figure 11.5 (paysage doux), plutôt que celui de
la figure 11.6 (paysage aléatoire).
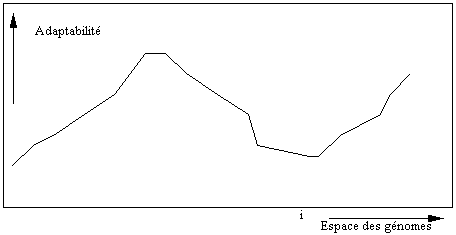
Figure 11.5 Un paysage d'adaptabilité doux.
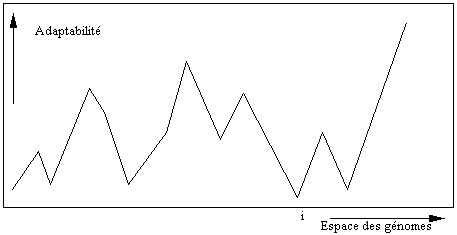
Figure 11.6 Un paysage d'adaptabilité
aléatoire.
Notre conjecture,
vérifiée par les simulations, est que n'importe quel choix d'une propriété
globale du réseau pour fixer l'adaptabilité conduit pour l'évolution des
espèces décrite par le système 11.4 à un comportement dynamique d'équilibres ponctués pour les petites
valeurs de m.
Sélection et évolution
Si nous partions d'une
situation initiale où toutes les espèces étaient présentes, la dynamique serait
très simple. Négligeons pour l'instant les mutations.
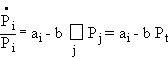
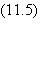
où Pt est la population totale. On voit que
la population des organismes adaptés, c'est-à-dire ceux dont l'adaptabilité est
plus grande que bPt, croît.
Mais la croissance de la population totale rend progressivement inadaptés tous
les organismes dont l'adaptabilité n'est pas maximum. Par conséquent, seuls
survivent les organismes d'adaptabilité maximum, dont la population finit par
se saturer. Les autres organismes disparaissent, à l'exception de ceux dont le
génome est voisin de celui des organismes adaptés, à cause des mutations.
En fait l'évolution des
espèces correspond au cas où, à l'origine des temps, seules quelques
populations existent sur Terre, dont aucune n'est la mieux adaptée. A cause des
mutations apparaissent d'autres organismes, dont le succès, c'est-à-dire la
population, dépend de leur adaptabilité comparée à celle des autres, des
ressources disponibles, et de l'histoire qui a pu privilégier l'apparition de
génomes voisins. En termes de dynamique, nous nous intéressons essentiellement
à des phénomènes transitoires, à des états métastables, bien plus qu'à la
recherche de l'équilibre.
11-3-2 Solution du système différentiel par la
méthode des perturbations
La phase de croissance
Supposons qu'au temps t =
0 un seul organisme soit présent. Sa population croît ainsi que celle des
génomes voisins peuplés par les mutations. Ceux des voisins dont l'adaptabilité
est plus grande croissent plus vite et leur population dépasse bientôt celle de
l'ancêtre originel. Pour les petites valeurs de m, un étroit nuage formé des
génomes les mieux adaptés se déplace dans l'espace des génomes vers un maximum
local d'adaptabilité. Cette dynamique est rapide. Si m est plus petit que b, la
mutation d'un prédécesseur vers un mutant mieux adapté se produit après la
saturation de la population du prédécesseur et le temps entre mutations obéit
à:
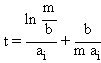
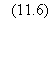
Pour
les valeurs intermédiaires de m pour lesquelles les mutations utiles se
produisent avant la saturation, l'intervalle entre mutations est de:
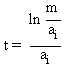
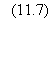
On observe dans les deux
cas une évolution accélérée: l'intervalle entre mutations décroît lorque
l'adaptabilité augmente.
La stase
Lorsque le maximum local
est atteint, un quasi-équilibre s'établit. La population des organismes de plus
grande adaptabilité se sature, et celle des organismes voisins s'alimente des
mutations en provenance du pic d'adaptabilité. La méthode des perturbations
permet de calculer chacune des populations au fur et à mesure que l'on
s'éloigne du pic. Le principe de la méthode s'apparente à celui des
développements limités. Le terme petit est m. On écrit qu'à l'équilibre tous les
premiers membres sont nuls et on ne garde dans les deuxième membres que les
termes de plus petit degré en m. On obtient alors une suite de relations:
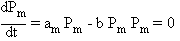
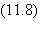
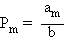
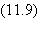
où l'indice m se rapporte au
maximum local.
Pour les premiers voisins
indicés v :
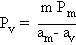
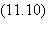
qui se généralise à la
distance d, le nombre de mutations ponctuelles entre le maximum et le génome i:
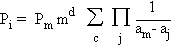
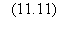
La somme s'étend à tous les
chemins de m à i en passant par les différents j.
Le paysage des
adaptabilités étant doux, ce qui est une conséquence de la robustesse, la
largeur de la distribution de population est plus faible que la distance entre
les maxima locaux. Les vallées sont donc
désertes, la probabilité d'apparition des mutants y est faible, et ils y
disparaissent rapidement à cause de leur faible adaptabilité. Le nuage de
population centré sur le pic, isolé des autres organismes, constitue une espèce,
c'est-à-dire un ensemble d'organismes dont les génomes peuvent différer
légèrement. Cette notion d'espèce apparaît donc comme une conséquence des
paysages d'adaptabilité doux, indépendamment d'une discontinuité de
reproduction entre deux partenaires sexuels trop différents.
L'absence de population
au fond des vallées est donc la raison de l'existence des stases.
L'apparition des nouvelles espèces
Pour qu'apparaisse un
mutant favorable, c'est-à-dire mieux adapté que les organismes qui occupent le
pic, il faut attendre un temps t de l'ordre de:
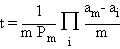
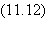
où le produit est pris
suivant le col, c'est-à-dire la ligne de plus grande pente qui joint le pic au
mutant favorable. Après l'apparition du mutant, le nuage de population quitte
l'ancien pic et dérive très vite vers le nouveau pic en remontant la pente à
partir du mutant favorable.
Simulations numériques
On peut simuler
l'évolution des populations d'organismes dont le génome est représenté par un
réseau booléen de six gènes-automates. Le graphe des interactions est
représenté sur la figure 11.7:
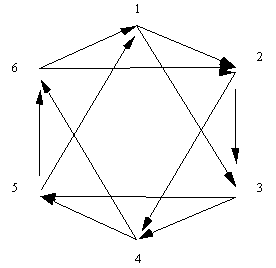
Figure 11.7 Structure de
connexions des réseaux booléens étudiés.
On se limite à quatre
fonctions booléennes NON-ET, OU, ET et NON-OU que nous codons respectivement
0,1, 2 et 3. Le nombre total des génomes possibles est 46 = 4 096. On mesure une propriété
dynamique comme la plus grande période
pour chacun de ces 4 096 réseaux. On n'autorise que les mutations
qui ne changent qu'une seule fonction à la fois, et l'on se restreint aux seuls
changements représentés par des flèches
ET <---> NON-OU <---> NON-ET <---> OU
<---> ET
Autrement dit, les
mutations autorisées ne changent que deux bits de la fonction de sortie. On
peut tester la robustesse de la période quand on décrit l'espace des génomes
par une suite de telles mutations. Le tableau 11.1 montre une section de cet
espace à six dimensions. Chaque case représente un génome i, et on a noté à
l'intérieur la période correspondante Ti.
Les génomes ont pour coordonnées 0023yx, où x est l'abscisse de la colonne,
indiquant la fonction de l'automate numéro 1, et y l'ordonnée de la ligne,
indiquant la fonction de l'automate numéro 2. 0023 signifie que les automates
6, 5, 4 et 3 ont respectivement comme fonction NON-ET, NON-ET, ET et NON-OU.
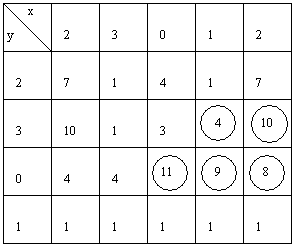
Tableau
11.1. Les plus grandes périodes Ti dans
l'hyperplan 0023yx de l'espace des génomes. Ce tableau fait déjà apparaître la
robustesse de la période, bien que le réseau soit relativement petit. Les deux
pics de coordonnées 002332 et 002300, et
de périodes 10 et 11, sont distants de trois mutations (les fonctions 0 et 3 ne
sont séparées que par une seule mutation). Le chemin de mutations le plus
favorable passe par 002302, le col, et 002301.
Les simulations dont les
résultats sont représentés sur la figure 11.8 ont été effectuées avec les
paramètres suivants:
m
= 2 10-5
, b = 10-7 , ai = 0,05 x Ti
Au temps t = 0, un seul
organisme de génome i = 002332 et de période maximum 10 est présent, sur un pic
local dont l'adaptabilité ai est
0,5 . On suit l'évolution de la population du génome initial ainsi que
celles des génomes "ensemencés" par les mutations (une dizaine
environ). On observe l'évolution vers le pic 002300 en quatre étapes
caractérisées par des régimes dynamiques différents:
• La première étape est la croissance exponentielle rapide (une
centaine de pas de temps) de la population centrée sur le premier pic. Une
première espèce est donc constituée de la population du pic de période 10 et de
ses deux voisins de périodes 4 et 8.
• La population saturée reste centrée sur le pic pendant 85 998 pas
de temps. C'est la stase. On voit apparaître et disparaître le mutant de
période 9.
• Au temps t = 85 998 apparaît pour la première fois le mutant
favorable de période 11 et de code 002300. Sa population croît donc
exponentiellement, dépasse celle de l'espèce précédente qui s'éteint à cause de
la compétition et devient un fossile.
• Une fois le nouvel équilibre atteint et la nouvelle espèce
constituée, on entre à nouveau dans un régime quasi statique.
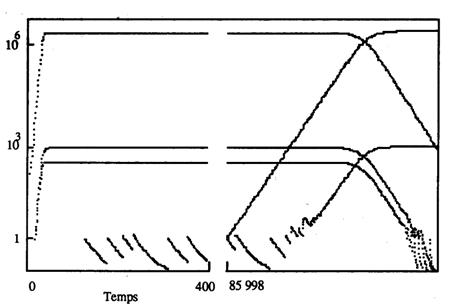
Figure 11.8 Simulation numérique de l'évolution des populations
d'organismes de génomes à six gènes. Le temps figure en abscisse et les
logarithmes décimaux des populations en ordonnée. L'intervalle compris entre
les temps 400 et 85 988 n'est pas représenté: les populations y restent
stationnaires au niveau atteint à t = 399. Aux temps inférieurs à 400, les
différentes courbes correspondent par ordre de population décroissante aux
génomes de période 10, 8, 4 et 9. Au temps t = 85 998 apparaît un organisme
mieux adapté de période 11 dont la population dépasse rapidement celle de tous
les autres.
On obtient des résultats
similaires pour une large gamme du paramètre m, et pour un choix différent de
la grandeur dynamique servant à déterminer les adaptabilités. Les pics peuvent
alors apparaître pour des réseaux différents, mais les propriétés
semi-qualitatives de la dynamique des populations, alternance des changements
rapides et des stases, restent les mêmes. Il en serait de même si l'on basait
les calculs des adaptabilités sur un modèle verre de spins comme celui
d'Anderson. Le modèle est donc très général; il repose sur des hypothèses
robustes et rend bien compte des équilibres ponctués observés par les
paléontologistes. C'est un modèle minimal en ce sens qu'il n'exige pas, pour
expliquer les faits, d'hypothèses nouvelles par rapport à la théorie
néo-darwinienne admise classiquement.
Nous discuterons au
chapitre 12 la portée générale des modèles basés sur des réseaux d'automates.
Il peut paraître très ambitieux de s'attaquer à des problèmes aussi profonds que l'origine de la vie ou
l'évolution des espèces avec des modèles aussi simplistes. En fait, aucun des
auteurs des modèles discutés dans ce chapitre ne prétend mettre un point final
aux controverses sur ces questions. Le but de ces modèles est de montrer qu'à
partir du moment où l'on prend en compte les interactions entre les gènes, même
par le modèle le plus primitif, on aboutit à des comportement dynamiques
semblables à ceux des systèmes vivants, et qui étonnent tant les biologistes
qui les observent.
Références
Le lecteur novice en
biologie moléculaire pourra se reporter à l'un des manuels classiques comme Biologie
moléculaire de la cellule, B. Alberts, D. Bray et al., Flammarion
(1987). Biologie moléculaire du gène, J. Watson, N. Hopkins et al.,
InterEditions (1989).
Le livre de J. Ninio, Approche
moléculaire de l'évolution, Masson (1978), décrit bien les questions posées
par l'origine de la vie et l'évolution. Celui de S. Kauffman, The Origins of
Order: Self-organization and Selection in Evolution, Oxford University
Press (1989), apporte des éléments de réponse originaux.
Le modèle de Kauffman est
décrit dans S. Kauffman, J. Theor. Biol., 22, pp. 437-467 (1969).
L'approche des
hypercycles a été proposée dans M. Eigen, Naturwissenschaften, 64,
p. 541 (1971).
Le modèle d'Anderson est
décrit dans P. Anderson, Proc. Nat. Acad. Sc., 80, p. 3386
(1983), et dans D. Rokhsar, D. Stein et P. Anderson, J. Mol. Evol., 23,
p. 119 (1986).
Comme ouvrage de référence
sur la génétique des populations standard, on pourra consulter Ewens W.J., Mathematical
Population Genetics, Springer Verlag (1979).
Le paradoxe des
équilibres ponctués apparaît dans S. Gould et N. Eldredge, Paleobiology,
3, p. 177 (1977), et l'idée de paysage d'adaptabilité dans S. Wright , Evolution,
36, pp. 427-443 (1982).

![]()
![]()