CHAPITRE 2

Définitions

Intuitivement, un réseau d'automates est un ensemble d'éléments en interaction. Pour simplifier au maximum les éléments de cet ensemble, notre première démarche est un retour aux mathématiques discrètes. Nous abandonnons donc, au moins pour l'instant, le continu. Commençons par le temps: au lieu d'être, comme en physique, une variable réelle, le temps, dans ce formalisme, est décomposé en intervalles égaux numérotés de 1 à n. Les variables, représentées par des automates, sont mises à jour au cours de chaque intervalle. Il est donc logique de représenter le temps par un entier naturel:

t = {0,1,2,3,.........,n,.........}

Remarquons incidemment que dans un ordinateur, le temps est également décomposé en intervalles par l'horloge qui cadence les changements d'état des unités logiques.

2-1 AUTOMATES

2-1-1 Définition classique

La deuxième opération de discrétisation concerne les variables continues et les équations différentielles qui sont remplacées par des automates d'états finis.

Figure 2.1 Un automate au sens de l'informatique.

En informatique, un automate est défini par la donnée de trois ensembles discrets:

I, l'ensemble des entrées i,

S, l'ensemble des états internes s,

et O, l'ensemble des sorties o,

ainsi que par deux applications:

S (i,s), la fonction de changement d'état qui donne le nouvel état au temps t+1 en fonction de l'entrée et de l'état au temps t,

et O (i,s), la fonction de sortie qui donne la sortie au temps t+1 en fonction de l'entrée et de l'état au temps t (Fig. 2.1).

Bien entendu, dans le cas général, les entrées, les états internes et les sorties peuvent être multiples et, dans les expressions des fonctions S et O , i, s et o figurent alors des vecteurs. L'important est que ces trois variables soient discrètes et donc représentées par des entiers ou des ensembles d'entiers. Le nombre des entrées d'un automate k s'appelle la connectivité d'entrée de l'automate.

Voici un exemple: un compteur d'impulsions peut être considéré comme un automate. Ses deux entrées sont l'entrée signal et l'entrée reset (remise à zéro). Lorsque l'entrée reset est à l'état 0 au temps t, l'état interne prend au temps t+1 la valeur qu'il avait au temps t, incrémentée par le signal au temps t. Le signal, quant à lui, peut prendre l'une des deux valeurs 0 ou 1. Si l'entrée reset est à 1, l'état interne prend au temps suivant la valeur 0.

Les sorties permettent de coder en binaire le nombre d'impulsions reçues depuis la dernière mise à zéro de l'état interne (voir dans l'appendice la correspondance codage binaire/codage décimal.) La sortie correspondant au bit le moins significatif (LSB: least significant bit) prend l'état 0 (respectivement 1) au temps t+1, si l'état interne au temps t est pair (respectivement impair). (En notation binaire, un bit est d'autant plus significatif qu'il correspond à une puissance de deux plus élevée. Par exemple, 5 est représenté par 0101: le bit le plus significatif est un 0 qui correspond à 8, la troisième puissance de 2, et le moins significatif est un 1, correspondant à 1, la puissance 0 de 2.) La sortie correspondant au bit le plus significatif (MSB: most significant bit) prend l'état 0 (respectivement 1) au temps t+1, si l'état interne au temps t est supérieur ou égal à 8 (respectivement inférieur à 8).

Le diagramme temporel indique l'évolution temporelle des états des entrées, de l'état interne et de l'état des sorties MSB et LSB. On notera les retards successifs entre les entrées, l'état interne et les sorties (Fig. 2.2).

Les circuits logiques de l'électronique digitale s'interprètent simplement en termes d'automates.

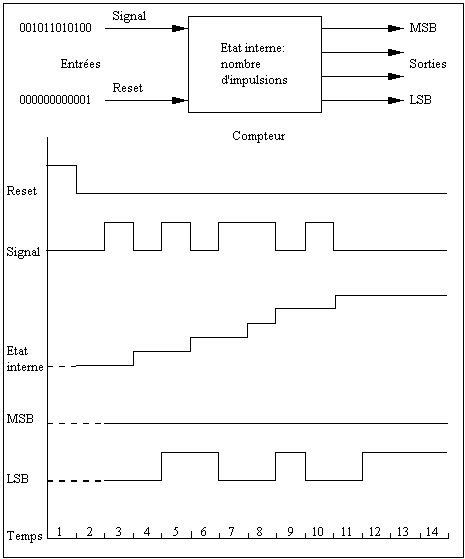
Figure 2.2 Ce compteur d'impulsions de 0 à 15 est un exemple d'automate à deux entrées binaires (sur le côté gauche), un état interne et quatre sorties binaires (sur le côté droit). Le diagramme temporel montre un exemple d'évolution de l'état interne et des sorties pour une séquence donnée de signaux d'entrée. Après avoir été mis à 0 par le reset, le signal interne compte les intervalles de temps pendant lesquels le signal est à 1. Les quatre sorties codent en numération binaire l'état interne au temps précédent. La sortie MSB ne passe à 1 que si l'état interne était supérieur à 8 au temps précédent, ce qui ne se produit pas au cours de cette séquence temporelle. La sortie LSB indique la parité de l'état interne: elle est à 1 si l'état interne était impair au temps précédent.

2-1-2 Définition simplifiée

En fait, dans les exemples traités dans ce livre, nous simplifierons la définition ci-dessus en ne considérant que des automates dont l'état interne et la sortie sont identiques.

Un automate simplifié sera donc défini par ses ensembles d'entrées et de sorties, et par la fonction de transition donnant la sortie au temps t+1 en fonction des entrées et éventuellement de l'état interne (c'est-à-dire la sortie) au temps t.

De plus, nous nous limiterons aux automates binaires, c'est-à-dire à deux états, par exemple 0 et 1.

2-1-3 Exemples

Nous travaillerons essentiellement avec deux types d'automates, les automates booléens et les automates à seuil que nous définissons ci-dessous. Le chapitre 4 sur les automates cellulaires contient d'autres exemples d'automates.

Les automates booléens

Les automates booléens opèrent sur des variables binaires, c'est-à-dire dont les valeurs sont 0 ou 1. En termes de logique, 0 et 1 correspondent respectivement à FAUX et à VRAI. Les fonctions logiques habituelles ET, OU, OU exclusif, sont des exemples de fonctions de transition d'automates booléens à 2 entrées. Un automate booléen à k entrées, dit de connectivité k, est défini par une table de vérité donnant l'état de la sortie pour chacune des 2^k configurations d'entrée. Suivant la manière dont on remplit la table de vérité on obtient l'un de ces automates qui sont au nombre de 2 à la puissance 2^k .

Prenons k = 2. Voici les tables de vérité de quatre fonctions logiques booléennes à 2 entrées:

ET OU OU exclusif NON-ET

Entrées 00 01 10 11 00 01 10 11 00 01 10 11 00 01 10 11

Sortie 0 0 0 1 0 1 1 1 0 1 1 0 1 1 1 0

Sur la ligne des entrées, nous avons représenté les quatre configurations d'entrée possibles, 00, 01, 10 et 11. Les quatre tables de vérité correspondent aux définitions habituelles des fonctions logiques: ET ne donne 1 que si ses deux entrées sont à 1 ; OU ne donne 1 que si au moins une entrée est à 1; OU exclusif ne donne 1 que si une seule entrée est à 1; NON-ET donne le complémentaire de ET. En termes de logique, A et B étant deux propositions, la proposition (A ET B) n'est vraie que si A et B sont vraies.

Le tableau 2.1 donne les tables de vérité, les codes décimaux (voir leur définition en appendice), et les noms des seize fonctions booléennes à deux entrées.

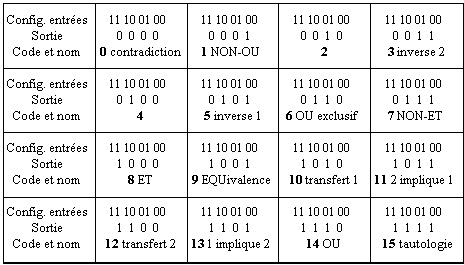
Tableau 2.1 Les seize fonctions booléennes à deux entrées, définies par leurs tables de vérité. Les noms sont ceux de la logique mathématique. Deux fonctions, codées 0 et 15, ont des sorties indépendantes des entrées. Quatre fonctions: 3, 5,10 et 12, ne dépendent que de l'une ou l'autre entrée qu'elles transmettent ou qu'elles inversent. Les fonctions 1, 4, 7, 8, 11 et 13 sont dites forçantes: pour une valeur de l'état d'une au moins des entrées, elles sont insensibles à l'état de l'autre entrée. Il suffit par exemple qu'une entrée de la fonction ET soit à l'état 0 pour que la sortie soit 0. Enfin, seules deux des seize fonctions, 6 et 9, nécessitent toujours la connaissance des deux entrées pour déterminer la sortie.

Les automates à seuil

La fonction de changement d'état x_i d'un automate à seuil i est définie par :

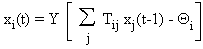
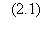
où Y est la fonction de Heaviside, égale à 1 si l'argument est positif ou nul, et à 0 sinon. La somme s'étend à tous les automates d'entrée j. Les T_ij représentent l'intensité des interactions entre l'automate j et l'automate i. Q_i est le seuil de l'automate i. Autrement dit, l'automate i prend l'état 1 si la somme pondérée ST_ij S_j des états des automates d'entrée est supérieure ou égale au seuil, et 0 sinon (Fig. 2.3).

Le choix des intensités des connexions T_ij et du seuil Q_i détermine la fonction de changement d'état, qui est obligatoirement une fonction booléenne. Une fonction à seuil peut donc se définir soit par ses connexions et son seuil, soit par sa table de vérité. Si le nombre des entrées est important, la définition en termes de connexions et de seuil est plus compacte que la table de vérité. En revanche, la table de vérité est plus rapide pour l'évaluation de la fonction.

A l'inverse, toute fonction booléenne ne peut pas se mettre sous la forme d'une fonction à seuil, comme nous le discuterons au chapitre 7.1 .

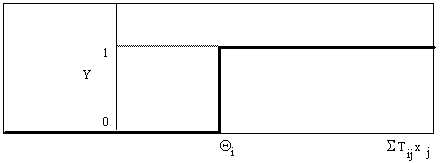
Figure 2.3 Une fonction à seuil. Si la somme pondérée des entrées ST_ij x_j est supérieure au seuil Q_i, la fonction vaut 1. Sinon elle vaut 0.

2-1-4 Automates et équations différentielles

Le lecteur connaît sans doute mieux les propriétés dynamiques des systèmes différentiels, qui servent par exemple à décrire les systèmes physiques en mécanique ou en électricité. Les réseaux d'automates peuvent être considérés comme une simplification des systèmes différentiels, obtenue par une discrétisation extrême. La première discrétisation, celle du temps, correspond au passage de l'équation différentielle à l'équation aux différences finies. C'est ainsi que:

dx/dt = f(x,y)

devient:

x(t+1) = x(t) + f(x(t),y(t))

La deuxième étape consiste à remplacer les variables réelles x et y par des variables binaires, c'est-à-dire des automates. L'opérateur 1+f de l'équation aux différences finies devient alors la fonction booléenne, à deux entrées x et y, de changement d'état de l'automate x.

La description en termes d'automates s'impose d'elle-même lorsque les composantes du système sont de nature discrète: atomes et molécules en physique, cellules en biologie. Il peut aussi arriver que l'on simplifie un système différentiel lorsque les variables continues subissent, du fait de la dynamique, des alternances de périodes quasi stationnaires séparées par de courtes transitions. C'est le cas par exemple des oscillations de relaxation observées dans les systèmes différentiels fortement non linéaires. Un exemple que nous rencontrerons dans cet ouvrage a trait à la biologie cellulaire: la concentration de certaines espèces chimiques à l'intérieur de la cellule est tantôt quasi négligeable, lorsque l'espèce n'est pas synthétisée, ou lorsque son transport à travers la membrane est bloqué, tantôt fixée à la saturation lorsque s'établit le régime pendant lequel cette espèce est utilisée. La concentration de cette espèce chimique peut donc être représentée par un automate, l'état 0 correspondant à la concentration minimum du produit, l'état 1 à sa valeur à saturation.

2-2 RESEAUX D'AUTOMATES

2-2-1 Propriétés structurelles

Un réseau d'automates est constitué d'un ensemble d'automates reliés entre eux de telle sorte que les sorties des uns soient les entrées des autres. C'est donc un graphe orienté dont les nœuds sont les automates et les arêtes les connexions dirigées de la sortie d'un automate vers l'entrée d'un autre.

On peut, bien entendu, considérer des réseaux ouverts ou fermés, suivant que certaines entrées des automates du réseau reçoivent des signaux d'éléments extérieurs au réseau. Le cas des sorties vers l'extérieur ne complique pas les propriétés dynamiques, mais il n'en est pas de même pour les entrées. Nous nous contentons pour l'instant de décrire des réseaux fermés, c'est-à-dire sans connexion avec l'extérieur.

La figure 2.4 représente le graphe des connexions d'un réseau de cinq automates booléens à deux entrées. Ce graphe correspond en fait à un ensemble de cinq relations logiques:

e(1) = OUex ( e(2) , e(3) )

e(2) = EQU ( e(3) , e(4) )

e(3) = ET ( e(4) , e(5) )

e(4) = EQU( e(5) , e(1) )

e(5) = OUex ( e(1) , e(2) )

où e(i) est l'état de l'automate i.

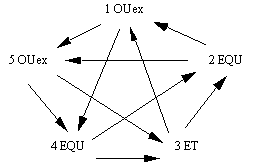
Figure 2.4 Un réseau d'automates de cinq automates booléens à deux entrées. Chaque automate possède deux entrées et transmet son signal de sortie à deux autres automates. Les fonctions OUex et ET ont été définies plus haut. La fonction EQU(ivalence) est la complémentaire de la fonction OU exclusif: elle ne donne 0 que si une seule entrée est à 1.

Structures de connexions

On est amené à considérer des structures de connexions variées. Les règles de connexion peuvent avoir un caractère aléatoire; dans ce cas la définition des entrées ne peut se faire que par la liste exhaustive des entrées de chaque automate: on parle alors de connectivité aléatoire. Nous serons aussi conduit à étudier le cas où chaque automate est connecté à tous les autres: la connectivité est alors complète. Enfin, la connectivité cellulaire présente un grand intérêt théorique et pratique: les automates sont répartis sur un réseau de petite dimensionnalité (1, 2 ou 3) et les connexions se font entre proches voisins (voir les deux chapitres suivants sur les automates cellulaires).

2-2-2 Propriétés dynamiques

Mode d'itération

La dynamique d'un réseau d'automates est entièrement définie par la donnée du graphe des connexions, celle des fonctions de transition des automates et enfin par la définition du mode d'itération. Il s'agit d'indiquer si tous les automates changent d'état en même temps, ou s'ils en changent l'un après l'autre, et dans quel ordre. Sans entrer tout de suite dans la description de toutes les variétés d'itération, donnons maintenant celle de l'itération parallèle: dans ce mode, tous les automates changent d'état en même temps en fonction de l'état des automates d'entrée au temps précédent:

x₁(t+1) = f₁( x₁(t), x₂(t),.................... x_N(t))

x₂(t+1) = f₂( x₁(t), x₂(t),.................... x_N(t))

...................................................................

x_N(t+1) = f_N( x₁(t), x₂(t),................... x_N(t))

où les fonctions f₁,f₂,...f_N sont les fonctions de transition des automates 1,2,...N. Cela par opposition à l'itération séquentielle, ou série, dans laquelle un seul automate à la fois change d'état. Une itération séquentielle est donc définie par la suite ordonnée des automates à modifier. Voici un exemple d'itération séquentielle:

x₁(t+1) = f₁( x₁(t), x₂(t),.................... x_N(t))

x₂(t+2) = f₂( x₁(t+1), x₂(t),................ x_N(t))

...................................................................

x_N(t+N) = f_N( x₁(t+1), x₂(t+2),.......... x_N(t))

Dans le cas de l'itération parallèle, la configuration 00000 a pour successeur, dans le réseau représenté sur la figure 2.4, la configuration 01010 (la convention consiste à représenter à gauche l'état de l'automate de numéro le plus élevé, de même qu'en notation décimale on fait figurer à gauche le chiffre de la puissance de dix la plus élevée). En revanche, dans le cas de l'itération série définie plus haut, le successeur de 00000 est 11010 au temps 5, après que tous les automates ont été mis à jour une fois et une seule (la différence entre les deux configurations tient à ce que, dans l'itération série, la mise à jour de l'automate n°5 se fait à partir des états déjà modifiés des automates n°1 et n°2).

Dans toute la discussion qui suit, ainsi que dans les chapitres 3 et 4, nous ne parlerons que d'itération parallèle.

Graphe d'itération

L'ensemble des états d'un réseau de N automates booléens comprend donc 2^N configurations possibles. On passe d'une configuration à une autre en appliquant la règle de changement d'état à chaque automate. La dynamique est donc entièrement décrite par le tableau des successeurs (le tableau 2.2 en est un exemple). Ce tableau a pour entrées l'ensemble des 2^N configurations du réseau, prises comme conditions initiales, et pour termes les configurations correspondantes au temps suivant.

A partir de ce tableau on peut tracer un graphe orienté, le graphe d'itération, dont les noeuds sont les configurations du réseau, et dont les arêtes orientées indiquent le sens des transitions d'une configuration du réseau au temps t à la configuration au temps suivant t+1.

La figure 2.5 représente le graphe d'itération du réseau précédent pour une itération parallèle. Ce graphe contient les 2⁵ = 32 états accessibles. Il illustre les traits dynamiques fondamentaux que nous définirons ci-dessous. C'est l'analogue des trajectoires dans la dynamique des systèmes continus (Fig. 2.6). On remarquera les analogies entre les différents attracteurs, points fixes et cycles limites.

Tableau 2.2. Tableau des successeurs. Dans la partie droite de chaque demi-tableau, figurent les configurations binaires et les codes décimaux des successeurs des 32 configurations initiales figurant à gauche, obtenus après une itération parallèle par le réseau de la figure 2.4 .

Attracteurs

Un réseau d'automates étant un système déterministe, si le réseau passe une deuxième fois par une configuration précédemment atteinte, la suite des états parcourus après le second passage est la même qu'après le premier. Le système décrit donc indéfiniment une boucle dans l'espace des états. Ces boucles s'appellent les attracteurs du système dynamique, et le temps de parcours de la boucle, la période de l'attracteur. Si cette période est 1, comme pour la configuration 8 dans le cas particulier ci-dessous, l'attracteur est un point fixe. On parle de cycle limite si la période est supérieure à 1. L'ensemble des configurations évoluant vers un attracteur donné constitue un bassin d'attraction. Le réseau pris ici comme exemple possède quatre bassins d'attraction.

La construction du graphe d'itération complet n'est évidemment possible que pour des réseaux de petite taille. Pour les réseaux de grande taille que nous utiliserons pour les applications décrites dans ce livre, on doit se contenter de décrire la dynamique du système en en caractérisant les attracteurs.

On peut essayer ainsi de déterminer:

• le nombre des différents attracteurs,

• leurs périodes,

• la taille des bassins d'attraction (le nombre des configurations qui évoluent vers l'attracteur),

• la durée des transitoires (c'est-à-dire le temps d'évolution depuis les jardins d'Eden, configurations sans prédécesseurs, jusqu'à l'attracteur).

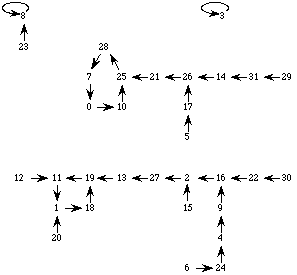
Figure 2.5 Graphe d'itération du réseau de la figure 2.4 (voir le tableau 2.2). Les numéros de 0 à 31 renvoient aux représentations décimales des 32 configurations binaires du réseau: le bit le plus significatif correspond à l'état de l'automate numéro 5; le moins significatif à celui de l'automate numéro 1. Les flèches indiquent la succession temporelle des configurations. On distingue quatre bassins d'attraction. L'état codé 3 est un point fixe isolé. Un autre point fixe est codé 8. Les deux autres bassins, plus importants, sont composés des configurations qui convergent ver le cycle limite de période 5 et celui de période 4.

La notion de distance est également très importante. La distance de Hamming entre deux configurations quelconques est le nombre des automates dans des états différents.

La simulation sur ordinateur est bien entendu un outil de choix pour ces études. C'est en fait la facilité de ces simulations par rapport à celles des systèmes différentiels qui motive le choix des réseaux d'automates comme modèles mathématiques. Nous verrons aussi que la théorie permet quelquefois de prévoir les propriétés dynamiques d'un réseau de structure donnée, comme dans l'exemple simple que nous allons discuter maintenant.

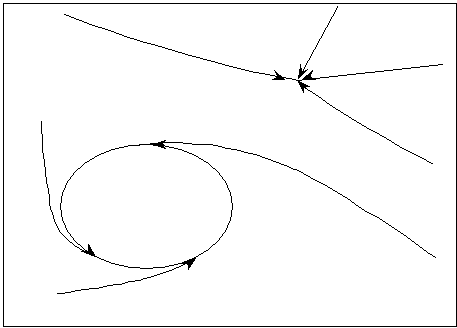
Figure 2.6 Trajectoires d'un système dynamique continu. On y voit deux bassins d'attraction, l'un vers un cycle limite et l'autre vers un point fixe.

2-2-3 Un cas simple: les "crabes"

Considérons un réseau d'automates à une seule entrée, dont les sorties identiques peuvent être multiples, comme celui représenté sur la figure 2.7.

Les différents automates booléens à une seule entrée sont au nombre de quatre.

Deux d'entre eux restent invariants à l'état 0 ou à l'état 1 quelle que soit l'entrée. Nous n'en parlerons plus par la suite. (Parmi les 2 puissance 2^k automates booléens à k entrées figurent toujours les deux automates invariants.)

L'un des deux autres transmet simplement le signal, c'est-à-dire l'état présenté à l'entrée; nous le noterons +. L'autre inverse le signal; nous le noterons -.

En connectant en réseau des automates à une entrée, on obtient comme sur la figure 2.7 des sous-réseaux indépendants ressemblant à des crabes. Des sous-réseaux indépendants peuvent apparaître dans des réseaux de plus grande connectivité; la probabilité de leur apparition est cependant plus importante, à taille fixée, pour les automates à une entrée.

La structure des sous-réseaux est tout à fait particulière: chaque sous-réseau comprend une boucle d'où sont issues des branches par lesquelles s'écoule le signal issu des boucles. Le signal ne peut entrer dans une boucle, car le nœud par lequel il rentrerait aurait alors deux entrées, une interne à la boucle, l'autre externe. C'est aussi la raison pour laquelle un sous-réseau ne comprend qu'une boucle: le sens de propagation le long d'une branche est défini par la boucle dont elle est issue; deux boucles ne peuvent donc pas être reliées par une branche. D'une manière imagée nous appellerons "crabes" les sous-réseaux, "têtes" les boucles et "pattes" les branches issues des têtes.

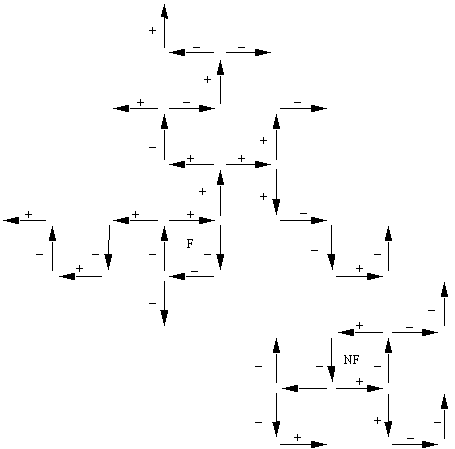
Figure 2.7 Réseau d'automates booléens à une entrée structuré en deux crabes. F indique une boucle frustrée, NF, une boucle non frustrée. Les flèches indiquent les connexions d'entrée et les signes + ou - la nature de l'automate situé à la pointe de la flèche.

La dynamique des états d'une patte correspond à la propagation d'un signal de l'entrée du premier automate vers le dernier automate de la patte. A chaque étape, ce signal est, soit transmis sans modification, soit inversé suivant la fonction de l'automate. A l'instant t, l'état du i-ième automate de la patte ne dépend que de l'état du premier automate de la patte au temps t-i. Si l'on part d'une configuration initiale quelconque, le transitoire ne subsiste que tant que le signal provenant de la configuration initiale se propage le long des pattes. En effet, dans le régime permanent qui est celui des attracteurs, le signal se propageant le long des pattes est celui issu de la tête du crabe. La longueur maximum du transitoire est celle de la plus longue patte du crabe.

Par la suite, tout est déterminé par la boucle de la tête. La période du crabe est donc celle de sa tête. Deux cas se présentent, suivant que le crabe est frustré ou non. Cette notion de frustration, plus sérieuse que pourrait le laisser entendre notre conte zoologique, a été introduite par F. Harari dans les modèles de relations entre individus en psychologie et par G.Toulouse dans la théorie des verres de spins dont nous parlerons plus loin. La frustration d'une boucle est définie par la parité du nombre de liaisons négatives de la boucle. Si ce nombre est impair, la boucle est dite frustrée; elle est non frustrée dans le cas inverse. Dans le cas d'une boucle non frustrée le signal qui a parcouru toute la boucle revient identique à lui-même après un tour. La période de la boucle est donc égale à m, le nombre des automates de cette boucle, ou bien à un diviseur de m dans le cas où la configuration de départ possède certaines symétries. En particulier, la période est égale à 1 si la configuration de départ est telle que l'état de chaque automate est la sortie correspondant à l'état de son automate d'entrée. Un crabe non frustré admet donc deux points fixes.

En revanche, dans le cas d'une boucle frustrée, le signal ne revient identique à lui-même qu'après avoir parcouru deux tours. La période de la boucle est donc de 2m pour les configurations sans aucune symétrie, et elle est un diviseur de 2m par un nombre impair dans certains cas particuliers. Un point important est qu'une boucle frustrée n'admet pas de point fixe.

L'étude théorique permet donc de déterminer la dynamique des réseaux booléens à une entrée : la longueur du transitoire, la période des attracteurs (c'est le plus petit commun multiple des périodes des crabes indépendants, ces périodes étant déterminées par la longueur et la frustration des boucles) et le nombre des attracteurs (c'est le produit du nombre des attracteurs de chacun des crabes — pour un crabe non frustré ce nombre est de l'ordre de 2^m/m, et de 2^m/2m pour un crabe frustré en négligeant les symétries). La taille des bassins d'attraction est du même ordre pour tous les attracteurs: elle est le produit de la période par 2^p, où p est le nombre total des automates des bras. Il n'y a donc pas de point fixe isolé.

Dans le cas particulier du réseau de la figure 2.7, le lecteur pourra vérifier qu'il y a deux crabes, l'un frustré et l'autre non. Le crabe non frustré a deux points fixes (configurations stables), un cycle limite de période 2 et trois cycles de période 4. Le crabe frustré a deux cycles de période 8. Le plus long transitoire dure sept intervalles de temps. Chaque bassin d'attraction contient un nombre de configurations égal à la période multipliée par 2³². L'ensemble de ces considérations nous permet donc de décrire la dynamique d'un réseau de 40 automates dont l'espace des configurations comprend 2⁴⁰ éléments, c'est-à-dire de l'ordre de 1 000 000 000 000 configurations.

Nous verrons par la suite que les cas que la théorie peut résoudre sont malheureusement exceptionnels. Qui plus est, les méthodes utilisables ne sont guère générales. Néanmoins, deux des notions que nous avons développées pour les crabes sont quelquefois applicables: celle des sous-réseaux indépendants et celle de la frustration. Notons à propos de cet exemple que la boucle est la structure la plus simple qui exige de prendre en compte l'ensemble des configurations du réseau pour en comprendre la dynamique. Dans le cas d'une chaîne ouverte, l'état des automates de la chaîne est déterminé après le transitoire par l'état du premier automate.