On choisit pratiquement toujours le mode d'itération parallèle.
Les premières études sur les réseaux d'automates, en particulier celle sur les automates autoreproducteurs de von Neumann, ont porté sur les automates cellulaires. Ce chapitre est consacré aux automates cellulaires les plus simples, ceux à une dimension.
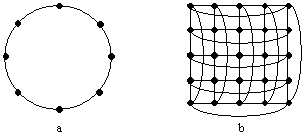
Figure 3.1
Structure périodique de connexion des bords. Les automates sont représentés par
des boules noires et leurs connexions par des traits. Les automates des bords
du réseau sont reliés entre eux. a) Une structure linéaire où les automates des
deux extrémités sont connectés. b) Un réseau carré, où les connexions bord à
bord sont représentées par les lignes courbes. Les automates du bord droit ont
comme voisins de droite ceux du bord gauche, et les automates du bord gauche
ont pour voisins de gauche ceux du bord droit. On peut remplacer, dans la
phrase précédente, "gauche" par "haut" et "droit"
par "bas".
3-2 Automates cellulaires a une dimension et a trois entrees
A une dimension le réseau est tout simplement une chaîne infinie d'automates. La structure de voisinage la plus simple comprend l'automate lui-même et ses deux plus proches voisins. Chaque automate a donc trois entrées et calcule son nouvel état à partir du sien propre et de celui de ses deux voisins. Une configuration d'entrée est donc représentée par un triplet de bits, le premier figurant l'état du voisin de gauche, le second celui de l'automate, le troisième l'état du voisin de droite. Il existe donc 23 = 8 configurations d'entrée différentes, et 28 = 256 règles différentes de changement d'état. Ces 256 règles sont numérotées de 0 à 255, nombres codant en notation décimale les huit bits de sortie correspondant aux huit configurations d'entrée (de 000 pour le bit le moins significatif à 111 pour le plus significatif).
Exemple: la règle 90 (01011010 en notation binaire) a pour table de vérité:
Configurations d'entrée 111 110 101 100 011 010 001 000
Sorties 0 1 0 1 1 0 1 0
Elle donne 1 pour les configurations d'entrée 001,011,100,110, et 0 pour toutes les autres.
Une manière très simple de visualiser la dynamique de ces réseaux consiste à utiliser une représentation où chaque ligne figure l'état du réseau à un temps t, le temps croissant d'une ligne à la suivante. Les figures (3.2) qui suivent montrent l'évolution temporelle de plusieurs réseaux cellulaires dans cette représentation proposée par S. Wolfram. La configuration initiale représentée sur la première ligne est choisie par un tirage au sort donnant pour chaque automate un état 0 ou 1 avec une égale probabilité. Dans chacun des cas la règle de changement d'état est référencée par son code décimal.
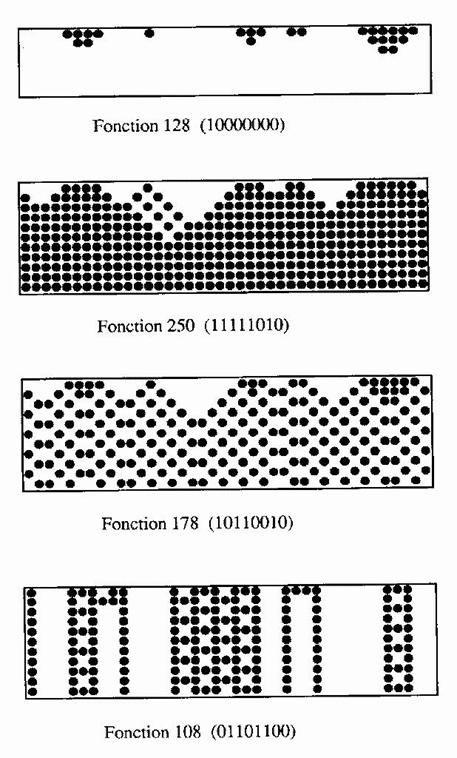

Figure 3.2 Itérations de réseaux linéaires d'automates
cellulaires à trois entrées. Les automates à l'état 1 sont figurés par des
boules noires, ceux à l'état 0 sont invisibles. Chaque ligne représente l'état
du réseau au temps t, et la ligne suivante son état au temps t+1. Le temps
croît de haut en bas. Dans tous les cas sauf un, la même configuration initiale
est itérée suivant une règle différente définie par son code décimal
(l'expression binaire de la table de vérité figure entre parenthèses). Seule la
règle 108 utilise une configuration initiale différente.
Ces figures font apparaître trois types de comportement, définissant trois classes de fonctions:
1. Certaines fonctions booléennes ont des attracteurs si "forts" que toute configuration évolue rapidement vers un état invariant homogène, composé de 0 (cas de la règle 128) ou de 1 (cas de la règle 250). Plus précisement, dans le cas de la règle 128 par exemple, à l'exception de la configuration ne comprenant que des 1, invariante dans l'itération, et qui constitue un point fixe isolé, toute configuration comprenant au moins un 0 évolue vers la configuration attractrice ne contenant que des 0.
2. Nous retrouvons le cas classique des attracteurs de périodes courtes, 1 ou 2 suivant les configurations initiales (règles 108 et 178). Le nombre des attracteurs différents est très élevé: il croît exponentiellement avec le nombre des automates.
3. Enfin, une situation relativement nouvelle est celle des périodes longues, trop longues pour être facilement observables (règles 90 et 126). Ces périodes croissent comme l'exponentielle du nombre des automates du réseau. La notion d'attracteur perd un peu de son sens dans ce cas.
Cette notion de période longue peut en fait être définie avec une certaine précision. Si, lorsque le nombre des automates d'un réseau varie comme N, la période moyenne varie comme une puissance de N, la période est considérée comme courte. Si cette variation est exponentielle, la période est considérée comme longue.
La structure spatiale révélée par la figure 3.2 dans le cas des périodes longues correspondant aux règles 90 et 126 mérite elle aussi d'être notée: nous observons une certaine régularité de "texture". Les triangles avec la pointe en bas se retrouvent en effet en plusieurs endroits. En fait, une étude statistique de cette figure ferait apparaître des structures fractales que l'on peut mettre directement en évidence à partir de conditions initiales particulières: par exemple une configuration dans laquelle un seul automate est dans l'état 1 (Fig. 3.3).
Les fonctions booléennes symétriques à trois entrées, c'est-à-dire celles qui font jouer un rôle symétrique aux entrées de droite et de gauche, appartiennent à l'une quelconque de ces trois classes. Les autres donnent le même type de comportement à une translation vers la droite ou vers la gauche près (voir l'exemple de la règle 20 sur la figure 3.4).
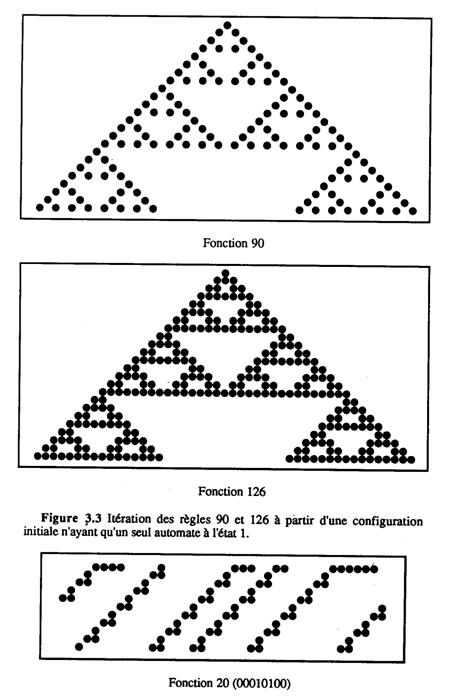
Figure
3.4 La règle 20 ne respecte pas la symétrie droite-gauche. L'attracteur, atteint après une seule
itération, a une période 2 à une translation vers la gauche près.
On peut bien entendu considérer des voisinages d'entrée plus importants, comportant par exemple cinq voisins, ou bien travailler avec des automates plus complexes à plusieurs états. Les comportements dynamiques observés appartiennent toujours à l'une des trois classes définies plus haut. Le livre de S. Wolfram, Theory and Applications of Cellular Automata, World Scientific(1986), donne de multiples exemples de ces automates cellulaires à voisinage et nombre d'états plus importants. L'une des questions encore ouvertes est l'éventuelle existence de comportements encore plus riches, nommés "calculateurs universels", sur lesquels nous reviendrons à propos des automates cellulaires à deux dimensions.
3-3 Automates cellulaires a une dimension et a deux entrees
Un cas particulier d'automates à trois entrées est celui pour lequel l'état de l'automate au temps t n'intervient pas dans la détermination de l'état au temps suivant. D'un point de vue fonctionnel, l'automate n'a donc que deux entrées. (Plus généralement, un automate à n entrées peut toujours être considéré comme un cas particulier d'un automate avec un plus grand nombre d'entrées.) On retrouve pour ces automates le même type de comportement que pour les automates à trois entrées: les trois classes précédentes sont en effet observées.
Notons que si le nombre des automates est pair, le réseau est en fait constitué de deux sous-réseaux fonctionnellement disjoints. Numérotons les automates. Au temps t, l'état des automates pairs (resp. impairs) ne dépend que de l'état des automates impairs (resp. pairs) au temps précédent. Ce sont ces mêmes automates pairs qui influeront sur l'état des automates impairs à l'instant suivant (Fig. 3.5).

Figure 3.5 Un réseau linéaire d'automates cellulaires à deux
entrées se décompose en deux sous-réseaux
indépendants dont les nœuds sont représentés ici par des ronds ou des croix.
En conséquence, seuls les automates de même parité interagissent à un instant donné, et le réseau se décompose en deux sous-réseaux indépendants. Il est commode alors de partir d'une configuration initiale composée de 0 pour l'un des sous-réseaux et de limiter l'analyse à l'autre. C'est ce qui est fait sur les figures 3.6 et 3.7.
Le nombre des fonctions booléennes à deux entrées étant limité à 16, il n'est pas très long d'en faire l'étude exhaustive. De plus, à chaque fonction on peut faire correspondre sa complémentaire, obtenue en inversant les sorties 0 et 1 pour chacune des configurations d'entrée. Les deux fonctions ont des graphes d'itération isomorphes, chaque configuration d'un graphe correspondant à la configuration complémentaire de l'autre. Nous pouvons donc, grâce à la symétrie 0/1, limiter notre étude aux huit fonctions du tableau 3.1 dont les codes décimaux varient de 0 à 7.
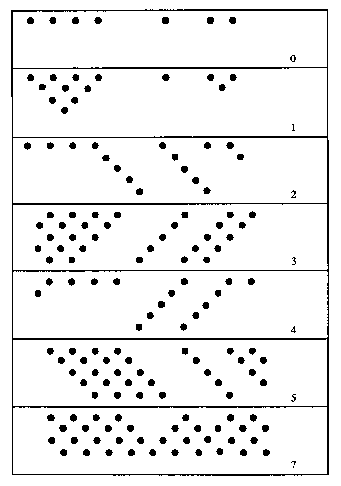
La même configuration initiale est itérée sur la figure 3.6 suivant 7 règles booléennes différentes donnant des attracteurs de période 1.
Deux de ces huit fonctions, de codes 3 et 5, ne sont en fait que des fonctions à une entrée qui ne font que transmettre l'une de leurs entrées, la gauche ou la droite. Toute configuration initiale est donc conservée à une translation près.
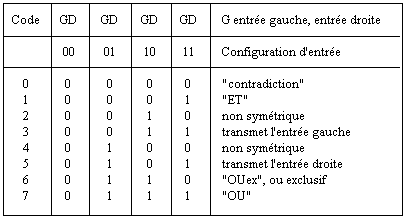
Tableau 3.1 Huit fonctions booléennes à deux entrées. Les huit
autres fonctions leur sont complémentaires.
La fonction de code 0 conduit, en une seule itération, quel que soit l'état initial, à la configuration dont tous les automates sont à l'état 0.
Les deux fonctions de codes 2 et 4 ont un rôle analogue: ce sont des détecteurs de différence entre les états des cellules voisines. La fonction 2 détecte la décroissance 10 de gauche à droite, tandis que l'autre détecte la croissance 01. A partir d'une configuration initiale quelconque, on obtient en une seule itération une configuration conservée par la suite à une translation près.
Les fonctions ET et OU, de codes 1 et 7, ont elles aussi un attracteur très simple: 0 partout pour ET, 1 partout pour OU. Les régions homogènes croissent régulièrement à partir des régions initiales de même type.
Seules la fonction OU exclusif, de code 6, et sa complémentaire EQUivalence, de code 9, donnent un comportement riche avec de très longues périodes (Fig. 3.7).
Figure
3.6 Itérations de réseaux linéaires
d'automates cellulaires à deux entrées.
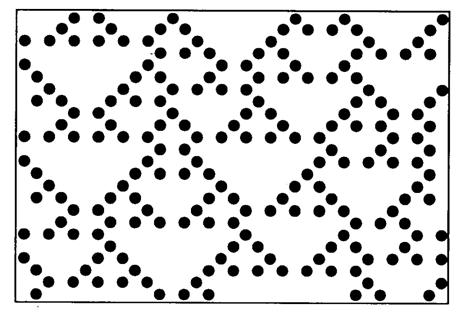
Figure
3.7 Itération de la règle OU exclusif.
Les réseaux d'automates cellulaires à une dimension constituent en fait des modèles d'école qui exhibent déjà une certaine variété de comportements malgré une grande simplicité de structure. Il est très facile de programmer leur dynamique et d'en observer l'évolution, sur un micro-ordinateur par exemple.
Références
Le livre de S.Wolfram, Theory and Applications of Cellular Automata, World Scientific (1986), contient une grande quantité d'études et de figures sur la dynamique des automates cellulaires à une dimension. Quelques méthodes algébriques, permettant de prévoir exactement l'évolution dynamique d'un réseau pour certaines fonctions de transition, y sont décrites.