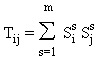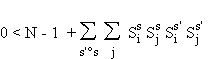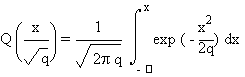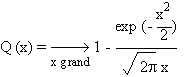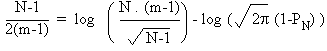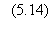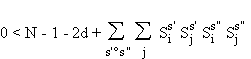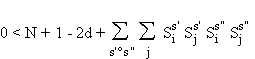Chapitre 5
Le modèle de Hopfield
Ce sujet a récemment
suscité un engouement explosif dans la communauté des physiciens des systèmes désordonnés.
Les raisons en sont simples:
• Le modèle que nous allons décrire est proche d'un autre modèle,
celui des verres de spins, utilisé par les physiciens pour décrire les propriétés
magnétiques des alliages dilués. Les alliages magnétiques dilués sont eux-mêmes
considérés par ces mêmes physiciens comme un modèle physique simple des milieux
désordonnés, comme les verres.
• L'existence d'une quantité analogue à une énergie permet
d'utiliser toute la puissance des méthodes de la physique statistique pour déterminer
les attracteurs.
• Il est possible de générer un réseau dont les attracteurs sont déterminés
à l'avance.
• C'est cette propriété qui permet au réseau "d'apprendre"
des configurations qu'il sera par la suite capable de "retrouver" à partir
d'une condition initiale pas trop éloignée de l'attracteur précédemment créé.
Nous disposons donc d'un
modèle sommaire de l'apprentissage et de la reconnaissance dans le cerveau, et
en plus d'un plan de câblage pour un système artificiel possédant les mêmes
propriétés.
La simplicité du modèle
permet d'en déduire théoriquement les propriétés les plus intéressantes. Nous développerons
donc dans ce chapitre quelques calculs basés sur une méthode très simple. Nous
reporterons au chapitre 8 l'exposé des résultats nécessitant l'usage de méthodes
plus sophistiquées empruntées à la mécanique statistique.
5-1 DEFINITION DU RESEAU
La version la plus simple
de ces réseaux, aujourd'hui appelés, peut-être un peu abusivement, "réseaux
neuronaux", est celle proposée par J. Hopfield en 1982.
L'unité de base est
l'automate à seuil, défini au chapitre 2. Ces automates ont été proposés par
McCulloch et Pitts dès 1943 comme modèles des cellules nerveuses (ou neurones).
Sous l'influence des autres neurones qui leur sont connectés, ces cellules
peuvent émettre des trains d'impulsions électriques.

Figure 5.1 Schéma d'un neurone (en haut) et de sa représentation
formelle (en bas). Le neurone est excité, ou inhibé, par les signaux reçus sur
ses synapses (à gauche de la figure). Ces signaux sont intégrés au niveau du
corps cellulaire, et si le niveau d'excitation est suffisant, un train
d'impulsions est émis le long de l'axone. A l'autre extrémité, à droite de la
figure, les ramifications de l'axone partent exciter d'autres neurones (non
représentés). Le neurone formel i somme les signaux reçus Sj pondérés par les poids synaptiques Tij et émet un signal Sj = +1, si cette somme est supérieure au seuil qi.
Une description simplifiée
du neurone consiste à le considérer comme un automate, à l'état 1 lorsqu'il émet
des trains d'impulsions, et à l'état 0 lorsqu'il reste au repos sans émettre. Les
entrées de l'automate figurent les synapses du neurone, c'est-à-dire les
connexions inter-cellulaires avec les neurones qui influent sur le taux d'émission
du neurone considéré (Fig. 5.1). Ces synapses peuvent être activatrices, c'est-à-dire
que si l'entrée est à 1, l'activité du neurone est renforcée, ou inhibitrices
dans le cas contraire. Un neurone i est donc représenté par un automate à seuil
dont l'état xi(t) est mis à jour
suivant:
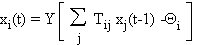
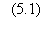
Y est la fonction de
Heaviside. La somme s'étend à tous les automates d'entrée j (voir le paragraphe
2.1.3 ). Les Tij, appelés poids synaptiques par référence
à la biologie, représentent l'intensité des interactions entre l'automate
d'entrée j et l'automate i. Les poids synaptiques positifs s'interprètent comme
des connexions excitatrices et les poids négatifs comme des connexions
inhibitrices. Qi est le seuil
de l'automate i. Autrement dit, l'automate i prend l'état 1 si la somme pondérée
STij xj
de l'état de ses entrées est supérieure ou égale au seuil, et 0 sinon.
Dans le modèle de
Hopfield la connectivité est complète à l'exception des termes diagonaux Tii qui sont nuls. Bien entendu, d'autres
termes non diagonaux peuvent éventuellement être nuls. De plus, les Tij sont symétriques ( Tij = Tji).
Chaque automate est donc défini par la donnée de ses poids synaptiques d'entrée Tij
et de son seuil Qi.
Le mode d'itération est le mode séquentiel aléatoire:
à chaque intervalle de temps un seul automate, pris au hasard, est mis à jour. Ce
choix correspond à l'idée qu'il n'existe pas dans le cerveau d'horloge interne
qui synchroniserait les transitions d'état des neurones. Ce mode d'itération,
dit de Monte-Carlo, est aussi fréquemment utilisé dans les simulations numériques
de certains systèmes physiques (voir le paragraphe 8.2).
Nous utiliserons dans ce
chapitre un changement de variable qui facilite les démonstrations. Nous
poserons:
S = 2x - 1 (5.2)
ce qui a pour effet de symétriser
la variable d'état. Si x = 0 , S = -1, et si x = 1 , S = 1. Ce changement de
variable conduit à changer le seuil en le remplaçant par 2 Qi - ∑Tij, et à diviser par 2 l'argument de la fonction de
Heaviside, ce qui est sans effet sur son résultat (N est le nombre des automates).
La fonction de changement d'état reste donc bien une fonction à seuil. Par conséquent,
si la somme pondérée des Sj (avec
les mêmes poids synaptiques) est supérieure au nouveau seuil, Si prend la valeur 1. Sinon Si prend la valeur -1.
5-2 ENERGIE ET POINTS
FIXES
Le caractère symétrique
des connexions et le choix de l'itération séquentielle permettent de démontrer
l'existence d'une fonction monotone au cours de l'itération. Nous pourrons donc
appliquer un théorème, dit de Lyapounov, qui démontre que les attracteurs sont
de période 1. L'"énergie" d'une configuration est définie, par
analogie avec l'énergie des systèmes magnétiques, par:
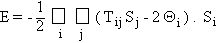
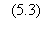
Lorsqu'un automate i
change d'état au cours d'un pas d'itération, la variation de la fonction énergie
s'écrit:
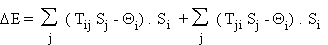
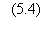
Dans cette expression, l'état
des automates est pris au temps t, c'est-à-dire avant l'itération. Le
renversement de l'automate i ne se produit que si le premier terme est négatif. En raison de la symétrie des poids
synaptiques, le deuxième terme de la somme est égal au premier; il est donc négatif
lui aussi. Par conséquent, à chaque itération, ou bien l'énergie reste fixe
lorsqu'il n'y a pas de changement d'état, ou bien elle décroît. Or l'énergie
est bornée en valeur inférieure, car la somme est finie. Par conséquent, au
bout d'un certain temps, une énergie minimum est atteinte, telle que la mise à jour
de chaque automate i conserve l'état de l'automate: la configuration atteinte
est donc un point fixe de l'itération.
Bien entendu, les points
fixes atteints n'ont pas de raison d'être identiques: ils dépendent de la
configuration initiale. De même, les énergies obtenues ne sont pas identiques. La
plupart ne sont que des minima relatifs.
Nous pouvons donc énoncer
le théorème suivant, dû à E. Goles-Chacc:
• Pour une itération série, les attracteurs
d'un réseau symétrique d'automates à seuil, à diagonale non négative, sont des
points fixes.
Cet auteur a également
montré, par des considérations analogues sur une quantité semblable à l'énergie,
que l'itération parallèle de ce type de réseau conduit à des attracteurs qui
sont soit des points fixes, soit des cycles limites de longeur 2.
Toutes les hypothèses sur
le réseau (poids synaptiques symétriques, itération séquentielle) sont nécessaires
pour que les attracteurs soient des points fixes, à l'exception de la nullité des
coefficients diagonaux Tii. En
fait, si ces coefficients sont positifs, le sens de variation de l'énergie
n'est pas modifié: en effet, DE ne faisant intervenir que les termes
rectangles de la matrice des connexions, il faut lui rajouter 2 Tii Si2 pour obtenir les deux termes négatifs
lors des changements d'état. DE reste donc négatif. En revanche, si les
Tii sont négatifs le caractère monotone de la
fonction énergie n'est plus assuré. Il suffit en effet que le coefficient Tii d'un seul automate soit négatif et supérieur
en valeur absolue à la somme de toutes les valeurs absolues des termes
correspondant aux autres automates qui lui sont connectés, et que son seuil
soit nul, pour que cet automate change d'état à chaque itération.
5-3 LA REGLE DE HEBB
On peut se poser, à propos de n'importe quel
type de réseau, le problème dit de la dynamique inverse:
• Est-il possible de construire un réseau d'automates
qui admette un ensemble de configurations quelconques comme attracteurs?
Autrement dit, nous nous
proposons de fixer à l'avance m configurations Ss, appelées références, que nous
souhaitons être les attracteurs d'un réseau dont les poids synaptiques et les
seuils sont à fixer en conséquence (l'indice supérieur s se rapporte aux références).
La règle de Hebb apporte une réponse partielle à ce type d'interrogation. Dans
son livre The Organization of Behavior (Wiley 1949), D. Hebb a suggéré que
l'apprentissage d'un comportement cognitif faisait intervenir au niveau
cellulaire le renforcement des synapses des neurones dont l'activité est corrélée.
Traduit en termes de réseau d'automates, cela revient à "construire" le
réseau par présentations successives des configurations de référence. Une présentation
consiste à fixer chaque automate dans son état dans la référence; on augmente
alors les Tij dont les
automates sont dans le même état, et on diminue les autres. Les Tij sont donc donnés par:
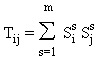
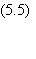
C'est la règle de Hebb.
Le choix des seuils est
particulièrement simple si:
• les références sont aléatoires: c'est-à-dire si l'état de
chaque automate Si est tiré au
sort avec une égale probabilité d'être -1 ou 1, indépendamment de l'état des
autres;
• les références ne sont pas corrélées: le produit Sis Sis' est
nul en moyenne si la référence s est différente de la référence s'.
Dans ce cas, si l'on utilise
les variables S, on prend les seuils nuls, ce que nous ferons dans la suite de
ce chapitre. Il n'est pas très difficile de généraliser les résultats que nous
allons décrire lorsqu'une ou deux des hypothèses ne sont pas vérifiées.
5-4 RESULTATS DE SIMULATION
Ces
choix permettent effectivement de construire un réseau dont les configurations
choisies comme références sont attractrices, à condition que celles-ci ne
soient pas trop nombreuses (de l'ordre de 0,1 N), qu'elles soient aléatoires (et
en conséquence, qu'elles comportent à peu
près autant de -1 que de 1) et qu'elles ne soient pas corrélées entre elles. Les
premiers résultats de simulation de Hopfield indiquent en effet que pour des réseaux
de 100 automates, avec 15 références choisies au hasard, on observe avec une très
forte probabilité les faits suivants:
• Si l'on prend une référence comme condition initiale, le réseau évolue
vers un attracteur qui soit est cette référence,
soit en est très proche: il ne diffère de la référence que par l'état de
quelques automates.
• Si l'on part d'une configuration initiale proche de la référence,
on converge vers l'attracteur de la référence, c'est-à-dire vers la référence
elle-même ou une configuration proche.
On peut illustrer ces
comportements à partir d'un système très simplifié de traitement d'images,
permettant une "mini-reconnaissance de caractères". Chacun des 858
= 64 éléments de l'image, appelé pixel (pour picture element),
est un automate à seuil relié à tous les autres. L'état du pixel est représenté
par sa couleur: noir pour l'état 1, blanc pour l'état -1. Les configurations
des automates sont aussi appelées "patterns" dans ce cadre. Les trois
patterns de référence figurent les lettres X, b et K. Le pattern X, par
exemple, correspond à la configuration représentée sur la figure 5.2:

Figure 5.2 Configuration représentant le pattern X.
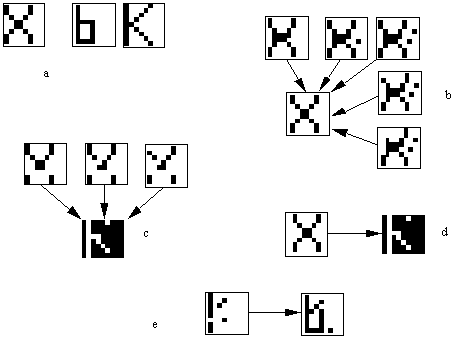
Figure 5.3 Exemples de convergence de configurations vers les
attracteurs d'un système de Hopfield. Chaque carré comprend 858 cases (ou pixels)
représentant chacune l'état d'un automate (les cases noires figurent les
automates à l'état 1, les cases blanches ceux à l'état -1). Les flèches partent
des patterns pris comme configurations initiales et pointent vers les
attracteurs correspondants. Les trois cases constituant la figure 5.3.a représentant
les lettres X, b, K ont été choisies comme références. Elles ont donc déterminé
le choix des connexions Tij du réseau, et sont invariantes dans la dynamique. On
voit que de petites altérations du pattern X sont corrigées par la dynamique 5.3.b.
D'autres, plus importantes, ne le sont pas
(5.3.c). La translation d'un pattern conduit vers un autre attracteur (5.3.d).
On note l'existence d'un attracteur mélange des deux patterns b et K (5.3.e).
La figure 5.3 représente
quelques-uns des résultats obtenus en faisant évoluer le réseau dont les poids
synaptiques ont été construits suivant la règle de Hebb à partir des trois références
X, b et K. On y observe que:
• Les trois références définies sur la figure 5.3.a sont invariantes.
• On a représenté sur la figure 5.3.b quelques configurations
appartenant au bassin d'attraction de la référence "X". On voit que
de petites altérations de la référence, obtenues en inversant quelques pixels
de la référence, sont "rattrapées" par la dynamique de convergence du
système.
• Remarquons sur la figure 5.3.c un autre pattern invariant, qui est
pratiquement l'opposé du pattern "K". En effet, la règle de Hebb avec
seuil nul est symétrique par rapport à l'inversion des patterns (l'inverse, ou
l'opposée, d'une configuration est obtenue en inversant les signes de tous les états
des automates; dans une représentation 0,1 on échange les 0 et les 1). Chaque
fois qu'un pattern est mémorisé, le pattern opposé l'est aussi. La légère différence
entre l'attracteur observé et l'opposé du pattern "K" est due à la
petite dissymétrie introduite par la manière dont on prend en compte le cas où l'argument
de la fonction de transition est égal à 0. C'est aussi une illustration du fait
que l'attracteur peut ne pas coïncider exactement avec la référence.
• Notons, figure 5.3.d, que la translation d'une référence n'est pas
une petite modification: elle conduit à inverser un grand nombre de pixels de
la référence, et la référence translatée n'est pas reconnue par le réseau,
comme le montre la figure.
• Enfin, sur la figure 5.3.e, apparaît un attracteur mélange de "b"
et de "K". L'existence de cet attracteur parasite sera expliquée au
chapitre 8 (paragraphe 8.4).
5-5 LA METHODE DU RAPPORT SIGNAL SUR
BRUIT
Trois méthodes permettent
de prévoir le comportement des réseaux de neurones à seuil construits suivant
la règle de Hebb, et d'expliquer les résultats des simulations. La plus simple
et la plus générale, bien que seulement approchée, est l'étude du rapport
signal sur bruit que nous allons développer maintenant. Les deux autres méthodes,
celle des répliques et celle des distances, plus rigoureuses mais plus
complexes, seront évoquées aux chapitres 8 et 11.
5-5-1 La règle fondamentale
La condition nécessaire
et suffisante pour qu'une configuration S(t) ait pour successeur la configuration
S(t+1), identique ou différente de S(t), s'écrit sous la forme de N inégalités
pour chacun des automates i:
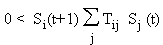
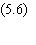
Ces inégalités sont la conséquence
directe de la relation (5.1) définissant la fonction de transition: si la somme
pondérée, argument de la fonction de Heaviside, est positive, Si(t+1) = 1 et le produit des deux est
positif; sinon les deux termes sont négatifs et leur produit est encore positif.
5-5-2 Invariance des références
Une configuration Ss est donc invariante, c'est-à-dire
est son propre successeur, si les N inégalités suivantes (une par automate i) sont
vérifiées:
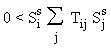
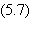
Les deux inégalités 5.6 et 5.7 sont valables quel que
soit le choix des Tij.
Si les Tij sont donnés par la règle de Hebb, l'inéquation
(5.7) devient:
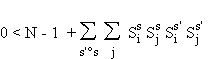
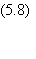
Nous avons remplacé Tij par son expression en fonction des références Ss. Le premier terme, N-1, dit terme de signal,
correspond au terme de la somme sur s' tel que s' = s. Chacun des N-1 termes de
la somme sur j est un produit de carrés de termes égaux à 1 ou -1 et vaut donc 1.
C'est ce terme de signal, grand, de l'ordre de N, qui assure l'invariance de la
référence.
La double somme comprend
q = (N-1).(m-1) termes égaux à 1 ou -1. S'il n'existe pas de corrélations entre
les différentes séquences, cette somme
vaut en moyenne 0. Son écart quadratique moyen est la racine du nombre de ses
termes, et tant que cette quantité est inférieure à N-1 l'inégalité a toutes
les chances d'être vérifiée. Ce terme est donc un terme de bruit.
Plus précisément, la
probabilité qu'une somme de q termes égaux à +1 ou -1 soit inférieure à x est
donnée par la fonction Q(x/\R(q)), définie par:
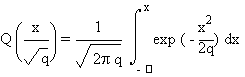

La figure 5.4 donne le
tracé de la fonction Q. La probabilité qu'une des inégalités (5.8) soit vérifiée
est donc:
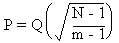
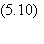
Par conséquent, en
choisissant un argument de la fonction d'erreur grand, il est possible de
rendre P aussi proche de 1 qu'on le souhaite. Soit y l'argument de la fonction
Q(y) correspondant à la probabilité P°. y varie en sens inverse de m. Le nombre
maximum de références donnant une probabilité d'invariance supérieure à P° est
donc:
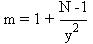
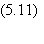
En première
approximation, m varie linéairement avec N.
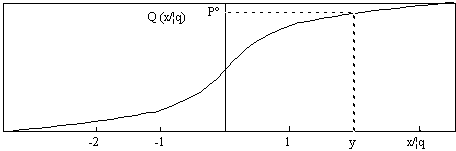
Figure 5.4 Probabilité Q(x/\R(q)) que le terme de bruit q soit
inférieur à x, terme de signal.
Invariance "approchée"
En fait il y a autant
d'inégalités que d'automates et la condition (5.11) ci-dessus n'assure que
l'invariance de P°N automates sur les N, c'est-à-dire le fait que l'attracteur
du réseau ne diffère de la référence qu'en (1‑P°)N automates. Autrement
dit, si on accepte que l'attracteur diffère quelque peu de la référence, on
s'attend à trouver une capacité maximum
m proportionnelle au nombre des automates. C'est la première loi d'échelle concernant
la relation entre le nombre de références et celui des automates. Le
coefficient de proportionnalité dépend de l'erreur sur la référence, c'est-à-dire
du nombre d'automates dont l'état n'est pas le même dans la référence et dans
l'attracteur. En réalité, lorsque la nombre de références atteint 0,14 N, bien
que l'erreur ne soit encore que de l'ordre du centième du nombre des automates,
on observe la "catastrophe des 14%": au-delà de cette proportion
aucune référence n'est plus retenue et les attracteurs sont sans rapport avec
les références. Cette discontinuité de comportement apparaît dans les
simulations numériques pour des réseaux comprenant un grand nombre d'automates (au
moins plusieurs centaines). Ce résultat important est prévu par la méthode du
champ moyen dont nous parlerons au chapitre 8 (voir les paragraphes 8.3.1 et 8.4).
Invariance "stricte"
Pour assurer que les N automates de la
configuration de référence sont invariants, il faut satisfaire N inégalités. Si
l'on admet que les doubles sommes sont indépendantes les unes des autres, ce
qui n'est qu'une simplification raisonnable, on obtient PN, la
probabilité que les N inégalités soient vérifiées:
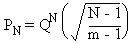
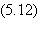
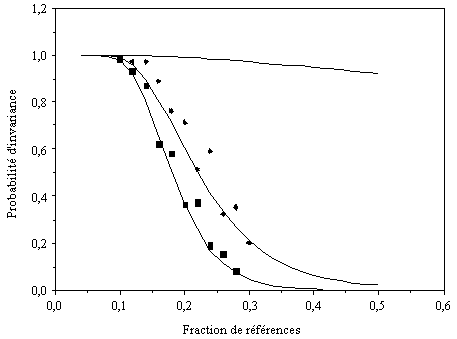
Figure 5.5 La probabilité d'invariance d'une configuration de
référence décroît avec le rapport du nombre de références au nombre d'automates.
Les losanges et les carrés sont des résultats de simulation numérique pour 50
et 100 automates respectivement. Les courbes correspondent à la formule théorique
(5.12). La courbe du haut correspond à la probabilité d'invariance d'un seul
automate suivant la formule (5.10).
P étant plus petit que 1, PN est plus petit que P, et une même
probabilité P° est obtenue avec un argument de la fonction erreur plus grand,
donc avec m plus petit (Fig 5.5).
5-5-3 Lois d'échelle
En utilisant le développement
asymptotique de la fonction Q(x) aux grands arguments
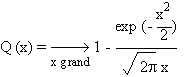
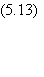
on obtient la relation suivante entre m, N et
PN:
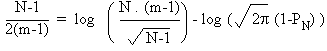
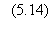
que l'on peut simplifier en
choisissant pour PN la valeur
qui annule le dernier terme (PN = 0,6). Aux grandes valeurs de N, en
première approximation m varie comme:
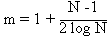
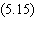
La relation est vérifiée
par les simulations numériques. Cette loi d'échelle en N/logN est la condition
d'invariance stricte des références.
5-5-4 Attractivité des références
L'une des propriétés les
plus intéressantes de ces réseaux est que les configurations voisines d'une référence
convergent vers cette dernière. Par configurations voisines on entend les
configurations dont seuls quelques sites diffèrent de la référence. Soit Ss"une
configuration voisine de la référence Ss ,
qui n'en diffère qu'en d sites. d est la distance de Hamming entre les deux
configurations. Pour un automate i non modifié, la condition (5.6) de retour en
un seul coup vers la référence s'écrit :
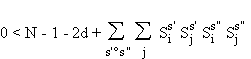
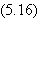
en utilisant la règle de Hebb.
Le terme de signal est donc diminué de 2d. La somme aléatoire est certes modifiée,
mais elle garde le même nombre de termes. Elle est donc inférieure au terme de
signal avec une probabilité:
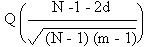
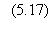
Pour un automate i modifié, le retour à la référence
en un coup se fait si:
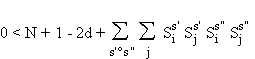
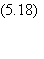
Un calcul précis de la
probabilité de retour à la référence exigerait que l'on tienne compte de ces
deux inégalités 5.16 et 5.18, et du fait qu'à chaque mise à jour d'un automate
modifié, la distance à la référence décroît. Contentons-nous simplement de
donner une borne inférieure de la probabilité:
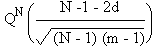
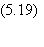
Une manière simple
d'obtenir la relation entre le nombre de références et la distance
correspondant à une probabilité d'attraction donnée, consiste à égaler
l'argument de la fonction Q dans l'expression ci-dessus avec celui donné précédemment
pour l'invariance stricte avec un nombre maximum m* de séquences (équation 5.12).
On obtient ainsi la relation suivante:
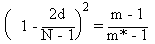
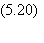
d, la distance d'attraction,
varie donc entre (N-1)/2 pour une seule référence, et 0 lorsque le nombre de références
est maximum (Fig. 5.6).
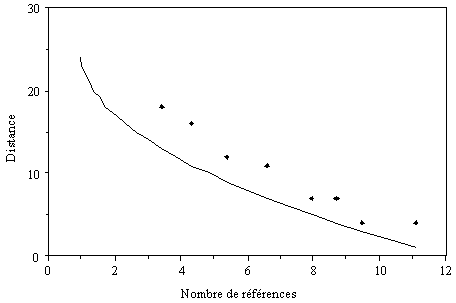
Figure 5.6 Distance à la
référence correspondant à une probabilité de 50% de retour à la référence, en
fonction du nombre de références, pour un réseau de 50 automates. Les points
sont des résultats de simulations numériques, et la courbe correspond à la
formule (5.20).
5-6 LE RESEAU DE HOPFIELD COMME MODELE DE SYSTEME
COGNITIF
Le réseau de Hopfield
n'est qu'un modèle très approximatif du fonctionnement cognitif du cerveau. Son
mérite essentiel est de permettre le passage du niveau cellulaire, modélisé par
les automates, au niveau cognitif modélisé par les propriétés dynamiques
collectives du réseau. Notons quelques-unes de ses propriétés.
L'information est répartie
dans le réseau. Cette notion n'a pas toujours été perçue comme allant de soi. Nombre
de modèles cognitifs du cerveau se fondent sur des variantes du modèle du
neurone "grand-mère". Dans ces modèles, une information particulière
est supposée être encodée dans une ou plusieurs cellules du cerveau: si un
sujet reconnaît, parmi différents visages, celui de sa propre grand-mère, c'est
parce qu'un petit groupe de neurones spécifiques
de la grand-mère ont été excités. Dans le modèle de Hopfield, au contraire, une
information est représentée par une configuration d'activité des neurones, et
la reconnaissance est interprétée comme le fait que le réseau admet cette
configuration comme attracteur.
Le processus de stockage de l'information est celui
d'une mémoire associative. Dans un ordinateur classique, les mémoires
sont dites à accès aléatoire, ce qui signifie que l'adresse à laquelle est
stockée une information est sans rapport avec celle-ci. Pour avoir accès à l'information
complète il faut connaître son adresse exacte, et toute information incomplète
est sans intérêt. Dans le cas d'une mémoire associative, une information
partielle permet de restituer l'information complète. C'est bien ce qui se
passe lorsque l'on présente au réseau d'automates une configuration initiale
proche de la référence: la dynamique du réseau restitue la référence.
Une autre propriété rapproche le réseau du cerveau
plus que d'un ordinateur classique, c'est sa robustesse. Si l'on
supprime une fraction des automates du réseau, les attracteurs ne sont guère
modifiés: les raisons de ce fait sont les mêmes que celles qui assurent la
convergence des configurations initiales vers les références les plus proches. Cette
propriété de détérioration graduelle des performances rappelle celle des
hologrammes en optique. Elle évoque aussi le fait que, malgré la perte de
plusieurs milliers de cellules nerveuses chaque jour, les performances du
cerveau ne déclinent que très lentement avec l'âge. Des destructions
comparables dans un ordinateur classique à la von Neumann auraient très vite
des conséquences catastrophiques.
Enfin, le processus d'apprentissage est purement local
et, pas plus que la reconnaissance, ne fait intervenir de processeur central.
En revanche, parmi les différences entre le cerveau et
le modèle de Hopfield, nous noterons l'hypothèse d'homogénéité du réseau. Personne
ne prétend aujourd'hui que la connectivité totale utilisée dans le modèle soit
celle du cerveau, que l'on sait fortement structuré. Cette hypothèse pourrait
cependant s'appliquer aux micro-colonnes, sous-ensembles de quelques milliers
de cellules complètement connectées du cortex cérébral.
Références
Le modèle de J. Hopfield
est décrit dans "Neural Networks and Physical Systems with
Emergent Collective Computational Abilities", P.N.A.S. USA,
vol. 79 (1982), 2554-2558. C'est un article remarquable par sa clarté et par
les questions qui y sont posées. Les problèmes du passage du neurone biologique
à son analogue formel sont en partie discutés dans P. Peretto: "Collective
Properties of Neural Networks: a Statistical Physics Approach", Biol. Cybern.,
50 (1984), 51-62 (un peu difficile).

![]()
![]()