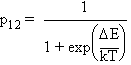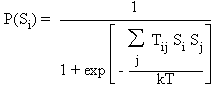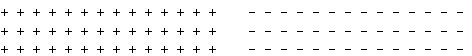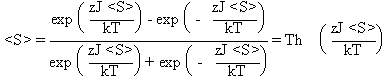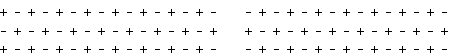Chapitre
8
Physique statistique
Les réseaux
à seuil décrits au chapitre 5 peuvent être généralisés
de plusieurs manières. L'une d'entre elles consiste à introduire
une probabilité de transition vers les différents états
possibles au lieu d'une fonction de transition. On parle alors d'automates
probabilistes, êtres mathématiques dont le comportement est
proche de celui des particules en physique statistique. Le rapide exposé
qui suit, et qui constitue la première partie de ce chapitre, n'est
pas une introduction à la thermodynamique statistique, mais une
reformulation de quelques notions utiles dans le cadre du formalisme des
réseaux d'automates. Cette reformulation nous permettra de comprendre
le lien existant entre les systèmes physiques et les réseaux
d'automates, en particulier en termes de simulation numérique. L'un
et l'autre domaines sont éclairés aux niveaux conceptuel
et méthodologique. C'est ainsi que l'approche de la physique statistique
permet de prévoir "exactement" les capacités de mémorisation
du modèle de Hopfield.
La
thermodynamique statistique résulte de travaux commencés
à la fin du XIXe siècle
par L. Boltzmann et W. Gibbs, puis poursuivis par M. Planck, A. Einstein,
P. Debye et bien d'autres depuis. Son objectif est de décrire les
propriétés des systèmes macroscopiques (c'est-à-dire
à notre échelle), à partir des propriétés
microscopiques de leur constituants élémentaires. On part
des hypothèses les plus simples concernant la répartition
des constituants entre les différents états microscopiques
qui leur sont accessibles. On peut alors obtenir par des moyennes les grandeurs
physiques mesurables caractérisant l'état macroscopique du
système. C'est le très grand nombre des constituants qui
permet de se contenter de moyennes, au lieu de rechercher toutes les configurations
en principe accessibles au système.
Nous ne discuterons
ici que de statistiques quantiques, dans le sens où les états
accessibles aux particules sont discrets. En fait, dans les exemples décrits,
il s'agira de spins d'Ising, notés Si,
variables binaires pouvant prendre les états-1
ou +1.
8-1 LES GRANDEURS FONDAMENTALES:
ENERGIE ET TEMPERATURE
Deux particularités,
l'existence
d'une fonction énergie et le rôle joué par la température,
caractérisent les systèmes physiques.
8-1-1 Energie et symétrie des interactions
A chaque configuration
peut être associée une fonction énergie.L'existence
de la fonction énergie provient des symétries internes du
système: les équations de la dynamique sont invariantes par
translation du temps et les interactions entre particules obéissent
à un principe d'égalité de l'action et de la réaction.
Ces symétries n'existent que parce que les interactions sont prises
en compte au niveau microscopique. Elle peuvent être absentes de
certains autres modèles utilisant des réseaux d'automates
dont les éléments à modéliser sont des objets
macroscopiques. C'est le cas en particulier lorsque ces éléments
sont des cellules vivantes, objets macroscopiques au regard de la thermodynamique.
A cause de l'analogie avec la physique, on s'habitue facilement, dans des
domaines très divers, à l'idée que toute dynamique
évolue vers un attracteur et que cet attracteur optimise une fonction
de la configuration du système. Ces analogies vont de l'économie
(maximisation des satisfactions), à l'évolution des espèces
(maximisation de l'adaptabilité). En fait, comme nous l'avons vu
dans le deuxième chapitre de ce livre, l'existence d'attracteurs
n'implique absolument pas celle d'une fonction de type énergie,
optimisée par la dynamique. Les chapitres 5, 8 et 9 ont la particularité
de porter sur les systèmes tels qu'existe une fonction à
optimiser, comme l'énergie.
Dans
le cas des spins, l'énergie s'écrit sous la forme d'une somme
de termes
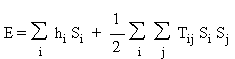
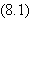
où hi est
le champ local appliqué au spin i etTij
la constante d'interaction entre les spins Siet
Sj.Si
la somme est restreinte aux termes linéaires en S, les particules
sont indépendantes. Les propriétés du système
et les méthodes de calcul sont beaucoup plus simples que celles
que nous allons évoquer à propos des systèmes en interaction,
pour lesquels les termes bilinéaires sont présents.
8-1-2 Température et probabilités
En général
un système physique n'est pas isolé du reste du monde. Même
s'il n'échange pas de matière avec l'extérieur, il
peut y avoir des échanges d'énergie. Ce type d'interaction
est pris en compte par la notion de température. Avec celle-ci
s'introduit la notion de probabilité. Bien que les propriétés
d'un système physique soient parfaitement déterminées
à l'échelle macroscopique, elles sont susceptibles de fluctuations
à l'échelle microscopique. La probabilité d'observer
une configuration a
d'énergie Ea
est donnée par le facteur de Boltzmann:
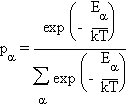

où T est la
température et k une constante appelée constante de Boltzmann.
La somme au dénominateur est effectuée pour l'ensemble de
toutes les configurations accessibles au système.
Aux
basses températures, les coefficients des exponentielles sont grands
en valeur absolue et les probabilités des configurations de basses
énergies sont donc très importantes par rapport à
celles des configurations de haute énergie. Plus la température
s'élève plus les configurations d'énergie élevée
interviennent.
A température
nulle le système évolue vers les minima d'énergie.
Sa dynamique rappelle celle du réseau d'automates décrit
au paragraphe 5.2: à un instant donné une particule "choisit"
l'état qui diminue ou garde constante l'énergie.
On retrouve aussi,
à température non nulle, un principe de minimisation. Le
système évolue de manière à minimiser une fonction,
dite énergie libre, donnée par:
F
= E - T . S(8.3)
où T est la
température et où S, l'entropie, estdéfinie
par
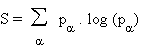
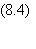
où pa
est la probabilité de la configuration a
d'énergie Ea.
L'entropie est d'autant plus forte qu'un grand nombre de configurations
sont accessibles au système. Son importance croît avec la
température. Aux basses températures, l'entropie n'intervient
guère, et les minima de l'énergie libre coïncident avec
ceux de l'énergie. Aux températures élevées,
la minimisation del'énergie
libre s'obtient par le fait que le système occupe avec des probabilités
non négligeables un grand nombre de configurations, même si
leur énergie est relativement élevée. C'est en ce
sens que la température favorise le désordre.
8-2 AUTOMATES PROBABILISTES
ET DYNAMIQUE DE MONTE-CARLO
Nous n'avons
évoqué jusqu'à présent que les aspects statiques,
c'est-à-dire les configurations stables de la dynamique. La question
peut se poser de décrire l'évolution d'un système
à partir d'une configuration initiale quelconque. Les informations
sur les énergies des différentes configurations ne suffisent
pas pour répondre à la question posée. Il faudrait
pour cela disposer d'informations sur les probabilités de transition
entre les différentes configurations du système. Bien entendu,
ces probabilités de transition, lorsque l'on est capable de les
évaluer à partir des connaissances physiques, sont fonction
de la température. En fait, si l'on ne s'intéresse qu'à
des propriétés qui ne dépendent que de la distribution
des probabilités d'occupation des différentes configurations,
on peut se contenter de simuler les probabilités de transition.
Le choix des probabilités de transition est alors dicté par
la nécessité qu'elles engendrent des probabilités
stationnaires de configurations obéissant à la loi de Boltzmann
(Eq. 8.2).
L'un des choix
possibles, la méthode du bain thermique, dérive d'une méthode
proposée par Glauber. On considère un système composé
d'éléments i en interaction les uns avec les autres. Soitune
configuration 1 d'énergie E1.
On se propose de calculer sa probabilité de transition vers une
configuration 2 voisine d'énergie E2,
qui ne diffère de la précédente que par la modification
de l'état d'un seul élément i. On choisit alors une
probabilité de transition donnée par
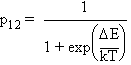
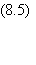
oùDE
est la différence d'énergie entre les deux configurations: DE
= E2-E1
(Fig. 8.1).
La probabilité
de transition est d'autant plus forte que l'énergie de l'état
final est inférieure à celle de l'état initial. Cette
préférence pour les basses énergies est d'autant plus
marquée que la température est plus basse. A température
nulle, la pente de la courbe est infinie, et l'on retrouve une dynamique
déterministe: le système évolue toujours vers les
états de plus basse énergie.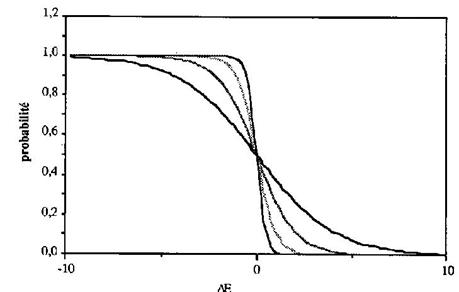
Figure
8.1la
probabilité de transition entre deux configurations voisines en
fonction de leur différence d'énergieDE
pour différentes valeurs de la température T. kT, défini
dans le texte,varie de 0,25 (la transition la plus abrupte) à 0,5
, 1 et 2 (la transition la plus douce).
Autrement dit,
la prise en compte de la température dans un système dynamique
se traduit par le caractère probabiliste des changements d'état
de ses composants. Ceux-ci ne sont donc plus décrits par des automates
déterministes mais par des automates probabilistes.
Un
automate probabiliste est défini par ses ensembles d'entrées
et de sorties, et par une probabilité de transition vers chacun
des états possibles de sortie en fonction des configurations d'entrée.
On
passe de la fonction de transition de l'automate déterministe à
la probabilité de transition de l'automate probabiliste en appliquant
la règle suivante:
*Suivant
un tirage au sort, l'automate prend l'état calculé par la
fonction de transition avec la probabilité p, et l'état complémentaire
avec la probabilité 1-p.
D'où l'idée
d'une méthode de simulation numérique permettant de trouver
les configurations de basse énergie d'un système physique
et de mesurer par la même occasion un certain nombre de grandeurs
physiques. On part d'une configuration initiale du système,choisie
de manière aléatoire, par un tirage au sort par exemple.
On tire au sort un élément i du système que l'on se
propose de faire éventuellement changer d'état. On évalue
la différence d'énergie entre les deux configurations 1,
celle où l'élément i est dans son état initial,
et 2, celle où i est dans l'état modifié. On en déduit
p12 par la formule 8.5
et l'on effectue la transition vers la configuration 2 avec la probabilité
p12. On réitère
cette procédure en tirant à chaque fois au sort l'élément
susceptible de changer d'état, jusqu'à ce que les propriétés
que l'on a choisi de mesurer se stabilisent, en moyenne. La méthode
s'appelle méthode de Monte-Carlo à cause des nombreux
tirages au sort qu'elle implique.
Avant de passer
à la description des systèmes magnétiques modèles,
précisons ici leurs liens avec les réseaux d'automates. Nous
nous intéressons aux systèmes physiques dont le paysage dynamique,
c'est-à-dire la carte des énergies, ne se réduit pas
à une vallée unique avec un seul attracteur d'énergie
minimum, mais aux systèmes comprenant de nombreuses vallées
séparées par des barrières, semblables en cela aux
réseaux de Hopfield dont les nombreux minima d'énergie correspondent
aux références. La température devient maintenant
un paramètre important qui contrôle les aléas de la
dynamique. Aux basses températures le système reste bloqué
au fond d'une vallée, en fonction des conditions initiales; lorsque
la température s'élève les excursions du système
en dehors du fond des vallées deviennent possibles, jusqu'à
ce que toutes les configurations du système deviennent accessibles.
8-3 LE MODELE D'ISING DU MAGNETISME
Nous
allons appliquer ces considérations aux propriétés
magnétiques de systèmes composés de moments magnétiques
élémentaires, les spins. Dans le modèle d'Ising, les
spins sont placés aux n?uds d'un réseau cristallin le plus
souvent à mailles carrées ou cubiques. Chaque élément
est donc caractérisé par son spin qui peut prendre la valeur
+1 ou -1, en fonction de ses interactions avec ses voisins. A chaque paire
de spins est associée une énergie d'interaction:
Eij
=- TijSiSj(8.6)
où Tij
est caractéristique de la paire considérée.
L'énergie
totale d'une configuration est donc donnée par:
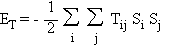
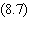
La somme est effectuée
sur tous les i et tous les j (d'où le facteur 1/2). LesTij
sont bien entendu symétriques et les termes diagonaux Tii
sont nuls.
Si la température
est nulle, la dynamique des spins est exactement celle que nous avons décrite
au chapitre 5 pour les automates à seuil. Les spins sont mis à
jour par une itération séquentielle aléatoire, et
chacun prend l'état qui minimise son énergie d'interaction
avec ses voisins. Il est donc amené à comparer la somme des
énergies des paires dont il fait partie à un seuil (nul en
l'occurrence) et à prendre l'état +1 si cette somme est négative
lorsque Si est positif
et-1 dans le cas inverse. Les attracteurs
sont bien des points fixes qui minimisent la fonction énergie.
Si la température
est non nulle, le comportement du spin n'est plus déterministe.
Il a tendance à "préférer" les états d'énergie
minimum, mais "l'agitation thermique" peut l'envoyer vers des états
d'énergie supérieure. D'une manière plus formelle,
le spin se comporte comme un automate probabiliste. Il transite vers l'état
Si avec une probabilité
donnée par:
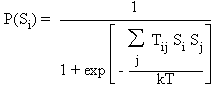

Autrement dit,lorsque
la somme des Tij Sj
est fortement positive (c'est-à-dire en valeur absolue grande par
rapport à kT), le spin Si prend
la valeur 1 avec une probabilité proche de 1. Lorsque la somme est
fortementnégative, cette
probabilité est quasi nulle et le spin prend donc la valeur -1.
Dans la zone indécise,
de largeur 4kT,le spin prend l'une
ou l'autre valeur.
Les propriétés
dynamiques du milieu magnétique dépendent du choix des Tij,
tout comme dans le cas des réseaux d'automates à seuil. On
peut choisir diverses connectivités: cellulaire, complète
ou aléatoire. Le modèle d'Ising est celui de la connectivité
cellulaire. LesTijpeuvent
être tous identiques, ou différents. Nous étudierons
trois cas, celui du ferromagnétisme (paragraphe 8.3.1), avec des
interactions identiques, celui des verres de spins (paragraphe 8.5), avec
des interactions complètement aléatoires, et la version probabiliste
des réseaux de Hopfield (paragraphe 8.4) qui constitue un cas intermédiaire.
8-3-1 Le ferromagnétisme
Description qualitative
Si toutes les
constantes d'interaction sont positives et identiques (Tij=
J), on parle de ferromagnétisme. Dans les deux configurations
qui minimisent l'énergie, tous les spins sont dans le même
état, +1 pour l'une d'entre elles, -1 pour l'autre (Fig. 8.2).
Figure
8.2 Les deux configurations d'énergie
minimum d'un ferromagnétique.
A température
nulle, en fonction de la configuration initiale, le système évolue
vers l'un ou l'autre attracteur. Lorsque la température s'élève,
la probabilité qu'un spin sorte de son trou d'énergie devient
non nulle, et de temps en temps certains spins prennent un état
qui n'est pas celui de la majorité de leurs voisins. Néanmoins,
on peut dire que les configurations accessibles au système restent
localisées dans une vallée autour de la configuration d'énergie
minimum. Au fur et à mesure qu'augmente la température, de
plus en plus de spins font des incursions vers des niveaux d'énergie
élevés, jusqu'à ce que le système soit capable
de passer d'une vallée à l'autre. Pour un système
de taille infinie, cette transition de phase se produit àtempérature
parfaitement définie. La phase de basse température, pour
laquelle le système reste toujours dans la même vallée,
s'appelle la phase ferromagnétique. Dans la phase de haute température,
le système passe allégrement d'une vallée à
l'autre au cours du temps et l'aimantation est nulle en moyenne. Cette
phase est appelée paramagnétique.
La méthode du champ moyen
Nous allons,
à titre d'exemple, expliciter une méthode de calcul analytique permettant
de suivre le changement de comportement du système en fonction de
la température. Cette approche, dite du champ moyen, n'est qu'une
approximation pour le modèle d'Ising, mais elle est d'un emploi
très général dans des cas beaucoup plus difficiles
que celui que nous allons traiter maintenant.
La probabilité
que le spin i soit dans l'état Ei
est donnée par la formule (8.8). On se propose de remplaçer
systématiquement Sj par
sa valeur moyenne (moyenne effectuée sur tous les spins), dans l'évaluation
de la somme sur j de toutes les interactions. Cette somme, J S
Sj , est équivalente
à un champ magnétique local appliqué au spin i par
ses voisins j , d'où le nom d'approximation du champ moyen. La moyenne
de Sj, que nous noterons
<S>, s'appelle aussi l'aimantation du système. Ei,
l'énergie du spin i,s'écrit
donc:
Ei=
-J z <S> Si (8.9)
où z est le
nombre de voisins du spin i. Ce nombre est de 4 pour un réseau carré,
de 6 pour un réseau cubique, etc.
<S>
est aussi la moyenne de Si
que l'on calcule alors comme:
<S>
= p+ . (+1)+ p- .
(-1) = p+ - p-(8.10)
oùp+
et p- sont les probabilités respectives que Si
soit égal à +1 ou -1.<S>
est donc solution de l'équation implicite:
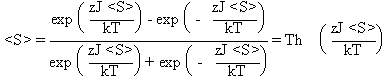
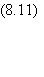
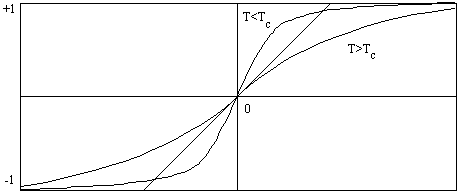
Figure
8.3Résolution
graphique de l'équation implicite de l'aimantation (8.11).
Le nombre de racines
de l'équation implicite en <S> dépend de la pente à
l'origine de la tangente hyperbolique comparée à 1 (Fig.
8.3). Cette pente varie en raison inverse de la température. Si
la pente est faible, la première bissectrice ne coupe la courbe
qu'en <S> = 0. L'aimantation est donc nulle à haute température.
Parcontre aux basses températures,
la pente est élevée et la première bissectrice coupe
la tangente en trois points. Le point d'aimantation nulle est en fait instable
car il correspond à un maximum de l'énergie libre ainsi que
le montrerait l'application directe des formules données plus haut
(Eq. 8.3 et 8.4). Les deux autres intersections correspondent à
des configurations stables. Les deux magnétisations opposées
sont d'autant plus proches de +1 ou de -1 que la température est
plus basse. La température de transition Tc
entre les deux comportements, paramagnétique à haute température
et ferromagnétique à basse température, est donnée
par :
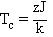
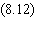
<S> joue le
rôle d'un paramètre d'ordre, nul dans la phase désordonnée
de haute température, et d'amplitude macroscopique dans la phase
ordonnée à basse température. Il prend l'amplitude
maximum de 1 à température nulle: l'ordre est maximum car
une seule configuration à la fois est accessible au système.
Les conclusions
de ce calcul approché restent valables lorsqu'on emploie des méthodes
plus sophistiquées. Elles sont aussi vérifiées expérimentalement.
En résumé:
*Aux
températures élevées, les configurations d'aimantation
nulle sont stables. Le système évolue entre elles car les
probabilités de transition entre des configurations d'énergie
voisine sont élevées. On dit que le système se trouve
dans une phase isotrope unique. Le paramètre d'ordre est
nul.
*Aux
basses températures, deux phases d'aimantation non nulle peuvent
exister et le système, du fait de la dynamique, "choisit" l'une
d'entre elles en fonction des conditions initiales (et du champ magnétique
extérieur qui peut priviligier l'une des deux phases dans un système
physique). Chaque phase est stable: un système de taille infinie
a une probabilité nulle de passer d'une phase à l'autre.
La symétrie du système entre les configurations d'aimantation
+1 et -1 est donc brisée à basse température. Le paramètre
d'ordre est non nul.
*La
transition entre les deux comportements se produit à une température
critique proportionnelle à l'interaction.
8-3-2 Généralisations
La physique des
milieux magnétiques est à l'origine de plusieurs généralisations
simples du ferromagnétisme.
Les interactions
entre spins voisins peuvent être uniformes et négatives. Le
milieu est alors appelé antiferromagnétique. Il y a deux
configurations opposées d'énergie minimum: dans chacune d'elles,
les spins sont alternativement positifs et négatifs lorsque l'on
passe d'un spin à son voisin immédiat (Fig. 8.4).
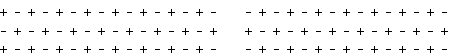
Figure
8.4 Les deux configurations d'énergie
minimum d'un antiferromagnétique. Elles sont équivalentes
à une translation près.
Bien que l'aimantation
totale soit nulle, le système est parfaitement ordonné. On
observe aussi deux régimes suivant la température, séparés
par une transition de phase. Dans le cas d'interactions avec les seconds
voisins, ou encore d'interactions anisotropes, on retrouve des comportements
avec transition de phase entre une phase désordonnée à
haute température, et des phases ordonnées à basse
température.
Nous n'avons parlé
jusqu'à présent que d'interactions uniformes dans tout le
réseau. L'introduction du désordre peut compliquer les choses.
Cependant, certains désordres ne produisent que des comportements
à deux attracteurs à basse température. Si toutes
les interactions restent positives, elles favorisent toujours le parallélisme
des spins et les deux configurations stables sont les configurations d'aimantation
proche de +1 et -1.
Il en est de même
pour le modèle de Mattis, pour lequel les interactions sont de la
forme:
Tij
= Ui Uj (8.13)
où les variables
Ui,distribuées
au hasard, valent +1 ou -1, ce qui rappelle un système de Hopfield
avec une seule référence. En effet, il suffit de faire le
changement de variable:
S'i = Ui
Si(8.14)
pour que la nouvelle
constante d'interaction entre les S'i devienne
égale à 1 et donc indépendante de la paire de spins
voisins considérée. Par conséquent, à basse
température, on retrouve deux attracteurs proches de S'i
= +1 et S'i = -1,
correspondant respectivement à Si =Ui
et Si= -Ui.
Bien entendu l'aimantation, liée aux variables Si,
n'a pas de raison d'être proche de +1 ou de -1. Le paramètre
d'ordre est à présent la projection de Si sur
Ui:
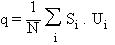
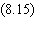
Suivant queS'i=
± 1, celui-ci sera proche de +1 ou de -1.
8-3-3 La frustration
En fait, un "simple"
désordre n'est ni nécessaire ni suffisant pour introduire
une multiplicité d'attracteurs. Il faut en outre que les boucles
d'interaction soient frustrées. Cette notion de frustration
est la même que celle que nous avons introduite au chapitre 3 à
propos des réseaux d'automates à une seule entrée.
Dans le cas présent, la frustration le long d'une boucle est évaluée
en faisant le produit des interactions des liens le long de la boucle.
Si ce produit est
positif, la boucle n'est pas frustrée. Il est possible de trouver
deux configurations opposées qui sont des minima absolus de l'énergie
de la boucle (Fig. 8.5).
Si le produit des
interactions est négatif, la boucle est frustrée et il n'est
pas possible de trouver une configuration qui satisfasse toutes les interactions.
Il existe en revanche plusieurs d'entre elles (huit au total pour des interactions
égales à +1 ou -1 comme sur les figures 8.5 et 8.6) qui satisfont
trois des interactions sur les quatre: leur énergie est donc de
?2 (Fig. 8.6).

Figure
8.5 Deux configurations d'énergie
minimum d'une boucle non frustrée. Les chiffres à coté
des liens figurent les constantes d'interaction, et ceux situés
aux quatre coins figurent l'état des spins. Pour les deux configurations,
l'énergie de chaque lien est bien négative et égale
à -1. L'énergie de la boucle est donc de -4
dans les deux cas.
Figure
8.6 Deux configurations d'une boucle
frustrée. L'énergie de la boucle est de -2 dans les deux
cas. Aucune configuration ne permet de minimiser simultanément les
énergies de chacune des quatre liaisons; il existe six autres configurations
d'énergie équivalente.
Dans le cas d'un
système dont aucune boucle n'est frustrée, comme pour les
deux exemples notés plus haut, l'ordre induit sur une boucle se
propage de boucle en boucle. Par contre dans le cas d'un système
frustré, c'est-à-dire comportant de nombreuses boucles frustrées,
les parties frustrées peuvent exister dans de nombreuses configurations
relativement indépendantes les unes des autres, d'où la possibilité
d'un très grand nombre d'attracteurs.
8-4 NEURONES FORMELS PROBABILISTES
Les réseaux
de neurones formels probabilistes ont un comportement intermédiaire
entre les systèmes ferromagnétiques décrits plus haut,
et les verres de spins pour lesquels les constantes d'interaction sont
choisies de manière complètement aléatoire. Les problèmes
posés par cette généralisation des systèmes
de neurones formels ont été étudiés par une
équipe composée principalement de D. Amit, H. Gutfreund et
H. Sompolinsky.
Il s'agit de spins
dont les interactions, comme dans le modèle de Hopfield, sont données
par:
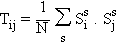
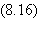
où le facteur
1/N a pour but de renormaliser l'intensité des interactions de manière
à ce que les résultats restent indépendants du nombre
des automates lorsque celui-ci tend vers l'infini. Les Ss
sont les configurations de référence. Il s'agit d'un système
à connectivité complète, contrairement au modèle
d'Ising pour lequel les interactions ne concernent que les proches voisins.
Rappelons que la
probabilité que l'automate i prenne l'état Si
est donnée par la formule (8.8), dans laquelle les poids synaptiques
sont ceux de la formule (8.16).
Cette probabilité
en fonction de Si correspond
à la fonction de l'énergie représentée sur
la figure 8.1. La température y joue donc le même rôle
en élargissant la zone d'incertitude. En particulier, à température
nulle P(Si) est dégénérée
en fonction de Heaviside, et le modèle probabiliste se ramène
à la dynamique déterministe du modèle de Hopfield
étudiée au chapitre 5.
Comme dans le cas
du modèle de Hopfield, on s'intéresse aux propriétés
de mémoire associative, et donc aux attracteurs de la dynamique
définis par le réseau des Tij
calculés suivant la règle de Hebb en fonction des références.
L'itération est de type séquentielle aléatoire. Les
attracteurs stricto sensu définis dans le cas des automates
déterministes doivent être généralisés.
On parle d'attracteur dans le cas d'une dynamique probabiliste, si le système
évolue autour d'une configuration attractrice sans s'en éloigner
de plus d'une distance de Hamming petite par rapport à N. Enfin,
dans la mesure où les interactions sont symétriques et les
référencesaléatoires
et non corrélées, les deux paramètres définissant
le comportement dynamique sont la température et a,
le rapport du nombre de références au nombre total des automates.
On peut bien entendu
utiliser les simulations numériques pour étudier les performances
d'un tel système. Leurs résultats sont en accord avec ceux
de l'étude formelle par les méthodes de la thermodynamique
que nous allons exposer maintenant.
Commençons
par introduire m grandeurs que nous assimilerons à des paramètres
d'ordre. Ce sont les projections des configurations attractrices Sa
sur lesréférences Ss:
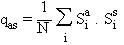
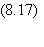
Autrement dit,
au lieu de calculer explicitement les configurations attractrices, on se
contente de calculer leurs projections sur les références.
Un attracteur proche d'une référence Smaura
alors toutes ses projections sur les autres références quasi
nulles (de l'ordre de 1/ );
la projection surSm
sera égale à 1.
);
la projection surSm
sera égale à 1.
qas
= d
(a,s)(8.18)
où d
est le symbole de Kronecker égal à 0 si a et s diffèrent,
et égal à 1 s'ils sont identiques.
L'étude
de D. Amit, H. Gutfreund et H. Sompolinskyest
basée sur l'existence de formules de champ moyen, analogues à
la formule donnant l'aimantation dans le cas du ferromagnétisme,
qui permettent de calculer les projections qas.
La connectivité étant infinie, ces formules sont exactes.
Différents types de solutions donnant des projections qas
non nulles apparaissent aux températures inférieures à
1.
Les solutions les
plus intéressantes sont très proches des patterns de référence.
Il correspond d'ailleurs à chacune d'entre elles une configuration
opposée. Elles ne sont cependant équivalentes aux patterns
de référence que si la température est nulle, et que
sia
tend vers 0, ce qui est en accord avec les résultats obtenus au
chapitre 5. Néanmoins, si l'on accepte un très léger
pourcentage d'erreur, de l'ordre de 1%, on observe des attracteurs dont
une seule des projections sur les références est proche de
1 et toutes les autres négligeables, pour des fractions du nombre
des attracteurs inférieures à environ 14% du nombre des automates.
Il existe cependant une fraction critique ac
au-dessus de laquelle les projections qas
sur les attracteurs s'annulent d'une manière discontinue. On peut
se faire une idée de la fidélité de la reconnaissance
des références en examinant la variation du pourcentage d'erreur
e, en fonction de a,
à température nulle. e est lié à la projectionqas
par:
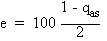
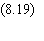
On voit que e n'augmente
que très lentement en approchant deac,
et qu'il reste toujours inférieur à 1%. Dès queac
est dépassé, e saute tout de suite à 50%, ce qui correspond
à des configurations non corrélées (Fig. 8.7).
On constate aussi
l'apparition de solutions "parasites" formées de la combinaison
de plusieurs références pour les températures et les
fractions a
les plus basses. La figure 5.3.e nous en a donné un exemple. Seules
les combinaisons d'un nombre impair de références sont stables,
mais toujours moins que les attracteurs proches des références.
Ces combinaisons sont obtenues en sommant sur chaque site les spins de
chacune des références: si la somme est positive le site
prend la valeur 1, sinon il prend la valeur -1. Le nombre des solutions
parasites est bien plus élevé que celui des références:
il est exponentiel en m.
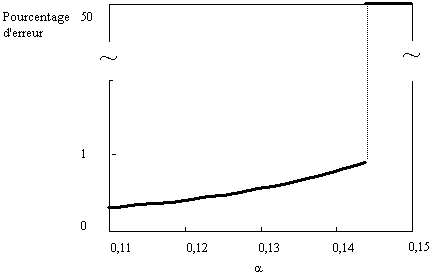
Figure
8.7 Fidélité de la reconnaissance
à température nulle. Le pourcentaged'erreurs
entre l'attracteur et la référence la plus proche reste faible
jusqu'à la "catastrophe". Après, c'est l'oubli total. (D'après
D. Amit, H. Gutfreund et H. Sompolinsky, Annals of Physics, 173,
30 (1987).)
En fait, augmenter
la température, ou augmenter a,
revient à bruiter la dynamique de convergence vers les attracteurs,
ce qui fait disparaître les plus instables. On peut donc tracer en
fonction des deux paramètres a
et T un véritable diagramme de phase dans lequel les lignes comme
TM et T3
séparent des phases de nature différente. Au-dessus de la
ligne TM on observe une
phase de type verre de spin, dans laquelle coexistent un très grand
nombre d'attracteurs dont la projection sur toutes les références
estpetite (de l'ordre de 1/\R(N)).
Sous la courbe TM apparaît
une phase où des configurations très proches des références
sont attractrices. Ce ne sont cependant pas les seuls attracteurs. Enfin,
si la température diminue en dessous de T3,
les mélanges de trois références deviennent stables.
On peut donc considérer qu'un certain niveau de bruit, représenté
ici par une température non nulle, peut améliorer les performances
du système comme mémoire associative en déstabilisant
les mélanges de références que l'on souhaite éviter.
Dans le cas des véritables neurones, ce bruit existe et a pour origine
les processus physico-chimiques à l'échelle membranaire.
Remarquons que le bruit thermique et le bruit lié à la présence
des autres références jouent le même rôle de
déstabilisation de la référence (Fig. 8.8).
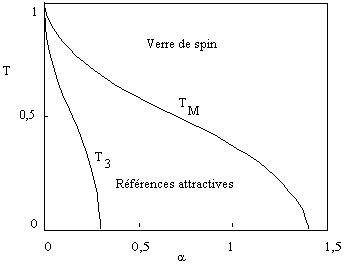
Figure
8.8 Diagramme de phase des réseaux
de neurones formels probabilistes. Trois phases apparaissent: à
température et nombre de références élevés,
une phase verre de spin. Dans la phase intermédiaire, les références
sont attractrices. A basse température et faible nombre de références,
les mélanges de références le sont aussi. (D'après
D. Amit, H. Gutfreund et H. Sompolinsky, Annals of Physics, ibid.)
8-5 VERRES DE SPINS
Les verres de
spins constituent un modèle des verres en général,
et des milieux magnétiques dilués en particulier. Les solides
peuvent exister sous deux formes extrêmes: la forme cristal, ordonnée,
correspond à un arrangement régulier des atomes, tandis que
la forme amorphe, désordonnée, est caractéristique
des verres. L'arrangement irrégulier des atomes se traduit au plan
macroscopique par des propriétés thermodynamiques différentes.
Par exemple, la transition de phase liquide-solide, appelée vitreuse
pour les amorphes, n'a pas le caractère abrupt que l'on observe
dans le cas des cristaux. La température de transition peut varier
dans le cas d'un refroidissement trop rapide, et les effets d'hystérésis
sont nombreux. Plutôt que de travailler sur des verres dans lesquels
le désordre de nature structurale est difficile à contrôler,
les physiciens travaillent souvent sur un système modèle
plus simple celui des milieux magnétiques dilués, dont on
peut contrôler la composition, et sur lequel un grand nombre de mesures
physiques sont possibles. Le désordre porte alors sur les interactions
magnétiques entre les spins.
Les verres de spins
ont été l'objet de nombreuses études tant théoriques
qu'expérimentales, et nous ne discuterons pas ici de ce qui relève
du magnétisme ou de la physique proprement dite. Par contre, nous
nous proposons de décrire les états métastables de
la dynamique, à titre de comparaison avec les autres systèmes
étudiés dans cet ouvrage.
Le
modèle de Sherrington Kirkpatrick est un système dans lequel
chaque spin interagit avec tous les autres d'une manière fixe mais
aléatoire, indépendamment d'une notion de distance. Cette
simplification justifie la méthode du champ moyen, et permet le
calcul des propriétés thermodynamiques par la méthode
dite des répliques, que nous n'exposerons pas ici. Les résultats
en sont les suivants.
La phase haute
température, ou phase paramagnétique, est tout à fait
comparable à la phase paramagnétique des systèmes
plus simples décrits précédemment: le système
a accès avec une probabilité finie aux diverses configurations.
Aux basses températures
apparaît une phase verre de spins dont les attracteurs sont caractérisés
par les propriétés suivantes:
*Le
nombre des attracteurs varie comme l'exponentielle du nombre des spins.
Il est de l'ordre de exp(0,2 N); ce résultat est démontré
à température nulle.
*Pour
caractériser le caractère ordonné de la phase verre
de spins, on souhaiterait déterminer un paramètre d'ordre
en projetant les attracteurs sur une ou plusieurs configurations de référence.
Du fait du désordre des interactions, cela n'est pas possible et
on est amené à considérer les projections croisées
des attracteurs entre eux. On définit qab,
la projection de deux attracteurs a et b, par:
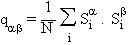
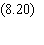
Au lieu d'un seul
paramètre d'ordre, comme dans le cas du ferromagnétisme,
ou d'un nombre fini comme dans le cas d'un réseau de neurones formels,
on est amené à définir une fonction d'ordre, l'histogramme
des qab :
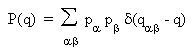
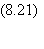
P(q) est la probabilité
que deux configurations a
et b
aient pour projection l'une sur l'autre q. pa
et pb
sont les probabilités respectives de a
et b,
et d
la fonction de Dirac. L'allure de P(q) est représentée sur
la figure 8.9.
On obtient deux
pics de Dirac à -qm et
qm et un continuum de
projections possibles entre les deux. (A haute température P(q)
n'aurait qu'un seul pic en q = 0.)
Figure
8.9 P(q), histogramme des projections
entre les attracteurs d'un verre de spins.
*La
distribution des attracteurs n'est cependant pas quelconque. Si
l'on considère
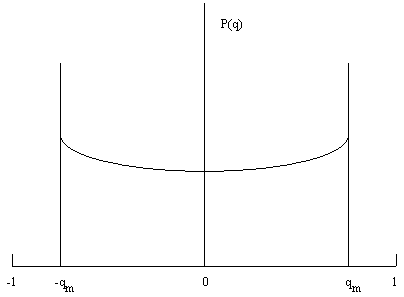
des triplets d'attracteurs abg,
leurs distances de Hamming respectives donnent des triangles qui sont soit
équilatéraux, soit des triangles isocèles dont les
deux côtés égaux sont toujours plus grands que le troisième
côté (Fig 8.10).
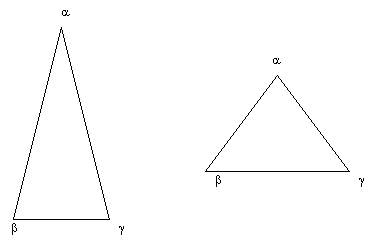
Figure 8.10 Les triangles caractéristiques
de l'ultramétricité.
Cette propriété,
qui définit l'ultramétricité, est caractéristique
des systèmes hiérarchiques.
La structure des
attracteurs est une structure hiérarchique en arbre, dans laquelle
les attracteurs sont représentés par les feuilles de l'arbre,
et leurs distances respectives par la hauteur de leur première racine
commune (Fig 8.11):

Figure 8.11 La structure hiérarchique
des attracteurs dans un verre de spins.
On voit ainsi l'origine
de la règle des triangles énoncée plus haut.
*Enfin,
malgré le très grand nombre des attracteurs, seul un petit
nombre d'entre eux ont un bassin d'attraction, et donc un poids statistique,
important. Les bassins de ces attracteurs occupent un pourcentage fini
de l'espace des états. Aux basses températures les propriétés
du système sont donc dues à l'un de ces grands bassins, à
condition tout au moins que le refroidissement du système ait été
effectué lentement.
Toutes les propriétés
énoncées plus haut ont été obtenues pour le
modèle de Sherrington Kirkpatrick. La question de savoir si ces
propriétés subsistent dans les systèmes physiques
réels, à trois dimensions, reste encore ouverte.
Références
Le livre de C.
Kittel etH. Kroemer Thermal Physics,
Freeman (1980), est une introduction simple à la thermodynamique.
Les articles les
plus importants concernant les sujets évoqués dans ce chapitre
sont réunis dans le livre de M. Mézard, G. Parisi et M. Virasoro Spin
Glass Theory and Beyond, World Scientific (1987).
![]()
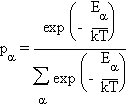
![]()
![]()
![]()