Chapitre 6
Au-delà du modèle de Hopfield
Le modèle de Hopfield est en fait un exercice d'école, instructif sur le plan théorique mais peu utilisable pour les applications pratiques. Comme modèle du cerveau, il serait basé sur des simplifications irréalistes en particulier:
• la connectivité totale et symétrique, fondée sur la règle de Hebb;
• le choix de références aléatoires et sans corrélations.
Comme dispositif technologique de reconnaissance et de mémorisation, il est limité par:
• une capacité en nombre de références faible: une fraction du nombre des automates (0,14 N si l'on accepte un faible taux d'erreur de l'ordre de 1%);
• la détérioration dramatique des performances dès que l'on tente de dépasser la capacité limite.
Nous nous proposons de décrire dans ce chapitre soit des variantes du modèle de Hopfield, soit des techniques analogues qui permettent de dépasser certaines de ces limitations. Nous commencerons par différents moyens d'augmenter la capacité d'un réseau, puis nous discuterons l'influence du relâchement de certaines hypothèses sur la connectivité peu compatibles avec les observations de la neurobiologie. Enfin, nous étudierons des variantes dont les attracteurs sont des séquences de références.
6-1 AUGMENTER LA CAPACITE
La quantité maximum d'information emmagasinée dans le réseau de Hopfield est, en nombre de bits:
m N = 0,14 N2 (6.1)
où m est le nombre des patterns et N celui des automates.
Par contre l'ensemble des connexions en contient de l'ordre de:
![]()
![]()
où l'expression entre crochets correspond à l'information, mesurée en bits, contenue dans une connexion d'amplitude maximale A codée en binaire (log2A), positive ou négative (+1).
La première évaluation est inférieure à la deuxième, ce qui revient à dire que le rendement du réseau peut être amélioré. Deux types d'approche permettant d'obtenir une quantité d'information plus proche du maximum théorique sont possibles:
• l'algorithme du perceptron et ses variantes,
• les méthodes algébriques.
Toutes deux sont en fait antérieures au modèle de Hopfield.
6-1-1 L'algorithme du perceptron
Le perceptron est une des premières "machines" à base d'automates, proposée pour la classification de patterns et capable d'apprentissage par la modification de poids synaptiques de neurones à seuil. Nous en discuterons au chapitre 7. L'algorithme que nous décrivons a d'abord été proposé pour cette machine, d'où son nom, mais son usage est assez général.
On part d'une matrice Tij quelconque, par exemple celle de Hopfield, mais ce n'est pas obligatoire. Pour chaque automate i et pour chaque séquence s , on teste la condition d'invariance en examinant le signe de la somme S
![]()
![]()
Si la somme S est positive, l'invariance est assurée (d'après l'équation (5.7)). On ne change donc pas Tij.
Sinon, on modifie l'ensemble des connexions des automates j vers l'automate i suivant la formule:
![]()
![]()
où la flèche indique le remplacement du membre de gauche par celui de droite.
L'algorithme se poursuit sur l'ensemble des automates, pour toutes les séquences, jusqu'à ce que la somme S soit toujours positive. On peut démontrer que la limite supérieure de la capacité, pour des patterns aléatoires non corrélés, est de 2 N . Remarquons que la matrice des connexions n'est plus nécessairement symétrique.
La même technique permet d'assurer l'attractivité des références. Pour qu'un pattern distant de la référence converge vers cette dernière en une seule étape, il faut que la somme S soit positive et la plus grande possible, d'après les arguments donnés au chapitre 5, équation (5.16). Cela permet d'assurer que le changement d'état de quelques automates ne suffit pas à modifier le signe de S. Une manière de réaliser cette condition consiste à vérifier les inégalités:
![]()
![]()
où K est un terme fixe qui garantit une convergence dans un rayon proportionnel à K. [Les propriétés du réseau sont invariantes si tous les Tij sont multipliés par un facteur constant; le rayon de convergence dépend donc de l'amplitude relative de K par rapport aux Tij; on choisit souvent de normer les Tij de telle sorte que la somme de leurs carrés par automate i soit égale à N, ce qui donne des Tij de l'ordre de 1; dans ce cas, le rayon de convergence est de l'ordre de K .] L'algorithme du perceptron s'utilise de la même manière que pour l'invariance, mais en testant l'inégalité (6.5).
Une variante, l'algorithme optimal, permet d'obtenir les plus grands rayons de convergence en limitant les modifications des Tij aux cas les plus défavorables: pour chaque automate i, on recherche la (ou les) référence(s) la plus instable, c'est-à-dire celle pour laquelle la somme S est minimale, et on applique la modification (6.4) jusqu'à ce que toutes les inégalités soient vérifiées, avec K le plus grand possible.
Interprétation géométrique
On raisonne indépendamment sur chacun des automates i, dans un espace de dimension N. A chaque référence s et à chaque automate i, correspond le vecteur his , de composantes hijs , tel que:
![]()
![]()
En abandonnant l'indice i, la condition de convergence (6.5) s'écrit:
![]()
![]()
Il faut donc que dans l'espace à N dimensions des {Tj }, la projection du vecteur T sur le vecteur hs soit positive et la plus grande possible. Pour que la condition soit vérifiée pour tous les hs , il faut que l'ensemble des hs soit situé à l'intérieur d'un cône d'angle au sommet aigu. Si les vecteurs hs sont aléatoires, on démontre que le cône ne peut contenir qu'un maximum de 2N vecteurs. Lorsque la condition 6.7 n'est pas vérifiée, l'algorithme du perceptron ramène le vecteur Tj vers l'intérieur du cône, jusqu'à ce que toutes les projections soient positives et les plus grandes possible (Fig. 6.1) .
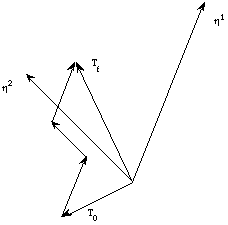
Figure 6.1
Dans cette interpétation géométrique, la règle de Hebb consiste à prendre comme vecteur T le barycentre des vecteurs h. Ce choix n'est pas le meilleur à cause des fluctuations d'orientation des vecteurs h. On peut montrer qu'en redressant le vecteur T pour tenir compte des vecteurs h les plus éloignés du barycentre suivant l'algorithme optimal, on aboutit pour T à l'axe du cône circonscrit aux vecteurs h (le plus pointu). Par contre, en utilisant la méthode algébrique décrite au paragraphe suivant (6.1.2), on aboutit à l'axe du cône passant par tous les vecteurs h.
6-1-2 Méthodes algébriques
Nous avons jusqu'à présent travaillé dans le cadre des automates, c'est-à-dire d'unités de calcul logiques, mais on peut se poser le problème de la reconnaissance par des réseaux d'unités analogiques, dont les variables sont continues. C'est cette approche, dont T. Kohonen est l'un des principaux auteurs que nous allons résumer ici, pour en comparer les résultats avec ceux de l'approche discrète.
Le problème de l'association
Soient deux ensembles de vecteurs {S} et {Y} que l'on se propose d'associer deux à deux. Ces vecteurs peuvent être par exemple des images, ou patterns, composées de pixels dont l'intensité varie continûment dans l'intervalle [0,1]. Les couples (S,Y) de patterns sont associés par une matrice T inconnue, à déterminer, telle que:
Y = T S (6.8)
(Les termes en caractères gras représentent des matrices. Si N est la dimension de Y, la relation (6.8) correspond à N équations scalaires.)
Si Y est différent de S, on parle d'hétéro-association. Si S et Y sont identiques, on parle d'auto-association. Réaliser l'auto-association revient à assurer l'invariance des patterns S par la multiplication par T. A ce stade le problème diffère donc de celui de Hopfield en ce que :
• les patterns sont des vecteurs dont les composantes sont réelles au lieu d'être binaires;
• la seule opération réalisée est la multiplication par la matrice T, analogue à une matrice de poids synaptiques; mais, pour l'instant du moins, il n'y a pas d'opération de seuillage, comme pour les automates à seuil, ni d'itérations multiples. L'opération n'est réalisée qu'une seule fois.
Pour calculer T, nous avons à notre disposition les m équations reliant les patterns d'entrée aux patterns de sortie. En regroupant ces équations on établit la relation matricielle:
Y = T S (6.9)
Dans les matrices S et Y, les lignes correspondent aux unités analogiques et les colonnes aux patterns. (La relation (6.9) correspond à N.m équations scalaires.) Si le nombre des patterns égale celui des unités analogiques on est ramené à un problème classique de l'algèbre linéaire que l'on résout en inversant la matrice S. Si le nombre des patterns indépendants est supérieur au nombre des automates, le problème n'a pas en général de solution. Nous exposerons ici, sans aucune démonstration, le cas où le nombre des patterns étant plus petit que celui des automates, l'inversion de la matrice S n'est pas possible.
La pseudo-inverse
La notion de matrice inverse, nécessaire à la résolution des équations (6.9) se généralise par celle de matrice pseudo-inverse dans le cas de matrices rectangulaires. La pseudo-inverse S+ d'une matrice S est définie par les trois conditions qu'elle vérifie:
• S S+S = S
• S+ S S+ = S+
• S S+ et S+ S sont symétriques.
On démontre l'existence et l'unicité de la pseudo-inverse. Si les colonnes de la matrice S sont indépendantes, la pseudo-inverse s'écrit:
S+ = (St S)-1 St (6.10)
où St est la transposée de S.
L'équation (6.9) en T a une solution exacte si:
Y S+S = Y (6.11)
ce qui est le cas pour des patterns linéairement indépendants, et aussi pour l'auto-association. La solution générale de l'équation (6.9) s'écrit alors:
T = YS+ + Z (I - S S+) (6.12)
où Z est une matrice quelconque. La solution de plus petite norme quadratique est:
T = YS+ (6.13)
(la norme quadratique d'une matrice est la somme des carrés de ses éléments.)
Si la condition (6.11) n'est pas vérifiée, les solutions (6.12) et (6.13) ne sont que des solutions approchées: elles minimisent la norme quadratique de la matrice d'erreur, Y - TS.
Dans le cas de l'auto-association, pour des patterns linéairement indépendants, on obtient donc:
T = S (St S)-1 St (6.14)
et le terme général de la matrice T s'écrit :
![]()
![]()
où Q est la matrice des projections croisées des patterns de terme général:
![]()
![]()
T s'interprète comme une matrice de projection sur le sous-espace vectoriel engendré par les patterns. La seule condition nécessaire pour effectuer ainsi le calcul est de pouvoir inverser la matrice Q: il faut donc que les patterns soient linéairement indépendants. C'est une condition beaucoup moins restrictive que la condition de décorrélation des patterns du modèle de Hopfield, qui est en fait une condition d'orthogonalité. Il s'ensuit que la limite supérieure du nombre des patterns est N, ce qui représente une amélioration notable. Remarquons que lorsque les patterns sont orthogonaux on retrouve pour T la règle de Hebb comme cas particulier.
Algorithmes de calcul de la matrice des connexions
Dans le cas général, celui des patterns quelconques, le calcul de T implique l'inversion d'une matrice qui peut être énorme lorsque l'on traite une application pratique. Il existe certes des méthodes itératives exactes permettant de calculer S+, comme par exemple la méthode de Gréville. On peut aussi se contenter de méthodes itératives approchées, comme la méthode de Widrow-Hoff.
La méthode de Widrow-Hoff
L'idée la plus simple est de rechercher une matrice W, a priori inconnue, telle qu'une fonction d'erreur quadratique E soit minimum. L'erreur élémentaire pour chaque unité de chaque pattern est le carré de la différence entre le pattern Y donné et le produit de S par W, l'approximation de la matrice T. La fonction d'erreur E, somme des carrés des erreurs élémentaires pour chacun des éléments i et pour chacun des patterns s, est donnée par:
![]()
![]()
On peut alors rechercher le minimum de E par une méthode de gradient (voir l'appendice) par rapport aux Wij:
gradwE = 2 ( W S - Y) St (6.18)
A partir d'une matrice W arbitraire, à chaque étape k de l'itération on change W, la matrice des poids synaptiques, suivant:
Wk = Wk-1 - lk ( Wk-1S - Y) St (6.19)
où lk, le paramètre de contrôle de l'algorithme, décroît à chaque itération. Remarquons la similitude avec l'algorithme du perceptron: les poids synaptiques ne sont modifiés que si la sortie calculée est différente de la sortie désirée.
La méthode de Widrow-Hoff, couramment utilisée, consiste à mettre à jour la matrice T après le passage de chaque pattern au lieu d'attendre la présentation de tout l'ensemble.
Les conditions pratiques de la reconnaissance
Du fait de la linéarité de la multiplication par T, une superposition linéaire de patterns de référence reste toujours en sortie une superposition linéaire. Il n'y a donc pas convergence vers l'un des patterns. On assure cette convergence en sortant du cadre linéaire. Dans la pratique, on revient à des procédures itératives sur un réseau. Le vecteur calculé TS peut par exemple être seuillé: chacune de ses composantes est appliquée à l'entrée d'un automate à seuil dont la sortie prend la valeur 1 si la somme est positive, et -1 sinon. L'application, multiplication par T suivie du seuillage, est alors itérée. Cette méthode ne diffère alors de la méthode de Hopfield que par le calcul des poids synaptiques.
Il semble en fait plus efficace d'utiliser, plutôt que des unités à seuil, des unités analogiques qui appliquent des fonctions continues comprimant la combinaison linéaire des entrées A=STijSj dans l'intervalle [-1,+1]. Deux fonctions possibles sont représentées sur la figure 6.2. La fonction représentée sur la partie gauche de la figure est linéaire par morceaux et vaut:
f(A) = -1 , si A < -1
f(A) = A , si -1 < A <1
f(A) = 1 , si A > 1
Le graphe de droite représente la fonction tangente hyperbolique:
![]()
![]()
Pour les réseaux d'unités analogiques, comme pour ceux composés d'unités logiques, le résultat obtenu par une application est itéré jusqu'à ce que l'attracteur soit atteint.
Les méthodes basées sur l'approche algébrique sont plus puissantes et mieux adaptées aux problèmes concrets de reconnaissance et de mémoires associatives que la méthode de Hopfield. Ces applications, ainsi que de nombreuses autres, sont décrites en particulier dans le livre de T. Kohonen. De très nombreuses variantes en ont été imaginées. Néanmoins, l'accroissement important du nombre des attracteurs possibles s'accompagne de quelques contraintes:
• Si le nombre des patterns approche celui des automates, les bassins d'attraction se réduisent pratiquement aux références.
• Les algorithmes exacts de cacul de T ne sont pas locaux. L'algorithme de Hebb ne nécessite, pour incrémenter une connexion, que la connaissance des activités des deux cellules connectées. La pseudo-inverse nécessite que l'on connaisse également la matrice des projections qui concerne l'activité de tout le réseau. Cette non-localité exige un transfert d'information à travers le réseau et représente donc un défaut en termes de réalisation pratique ou de modélisation du cerveau. Seul l'algorithme de Widrow-Hoff conserve une certaine localité.
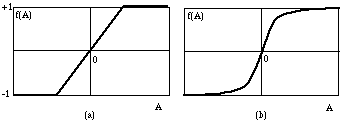
Figure 6.2
6-1-3 Changer la connectivité
Peut-on augmenter encore la capacité mémoire? La réponse est oui, mais à condition de changer certains principes de construction.
Connexions non linéaires
On peut augmenter la capacité du réseau en prenant comme signaux d'entrée des combinaisons multilinéaires des états des autres automates. Nous traiterons le cas des signaux bilinéaires suivant les notations et l'approche du rapport signal sur bruit déjà développées au chapitre 5.
xi(t) , l'état de l'automate i au temps t, est donné par :
![]()
![]()
Les connexions ternaires sont calculées à partir d'une généralisation de la règle de Hebb:
![]()
![]()
L'analyse du rapport signal sur bruit s'applique donc facilement. La condition d'invariance des références s'écrit:
![]()
![]()
que l'on décompose en :
![]()
![]()
Le premier terme de signal n'est supérieur au bruit d'écart quadratique moyen N que pour :
m < a N2
(On peut même démontrer par d'autres méthodes que a est de l'ordre de 0,08.) La capacité du réseau est donc proportionnelle au carré du nombre des automates, à condition d'admettre un pourcentage d'erreur petit mais fini. Bien entendu, ceci n'est pas miraculeux. Le nombre total des connexions a été considérablement augmenté: il est de l'ordre de N3. D'une manière générale, le nombre des attracteurs d'un réseau d'automates à seuil construit suivant une règle d'apprentissage "à la Hebb" varie comme la connectivité des automates. Nous en verrons plus loin d'autres exemples.
Architecture modulaire
Nous n'avons discuté jusqu'à présent que de réseaux homogènes. En structurant un réseau en sous-réseaux indépendants, il est possible d'obtenir un nombre exponentiel d'attracteurs.
Supposons N automates répartis en N/p sous-réseaux de p automates chacun. Chaque sous-réseau possède un nombre d'attracteurs indépendants de l'ordre de ap, et le nombre des attracteurs différents du réseau global est de
(ap)N/p
Bien entendu, le processus de division peut être poursuivi plus loin et les sous-réseaux eux-mêmes divisés en sous-sous-réseaux... A la limite, un ensemble de N automates déconnectés possède 2N configurations stables! Mais ces configurations ne sont pas attractrices. Le processus de hiérarchisation doit s'arrêter à un niveau tel que le nombre des automates du plus petit module assure l'attractivité des configurations de référence, et que la multiplicité des sous-réseaux permette d'emmagasiner le plus grand nombre de références.
Cette approche modulaire est celle que nous observons dans le cerveau divisé en aires corticales, elles-mêmes divisées en colonnes et en micro-colonnes. En ce sens, le modèle de Hopfield avec connectivité complète est plus proche d'une micro-colonne de quelques dizaines de milliers de neurones que du cerveau tout entier.
Les réseaux structurés n'ont guère été étudiés jusqu'à présent, que ce soit au niveau des applications ou à celui des principes. L'un des problèmes qui se posent est celui de la spécialisation des sous-réseaux. L'amélioration des performances du système suppose en effet que les attracteurs des différents sous-réseaux soient différents. Cette différence peut être fixée au départ. Dans le cas d'un système de traitement d'image, on peut faire en sorte que les cellules de chaque sous-réseau soient sensibles à des traits caractéristiques différents: positions des points, orientations des contours, mouvements, couleurs.... Par conséquent, la même image est traitée suivant des critères différents par chaque sous-réseau et après apprentissage, les attracteurs des sous-réseaux sont quasi indépendants. Encore une fois, cela semble être le cas de l'aire visuelle 17 du cortex, où l'on observe plusieurs cartes du champ visuel sensibles à des traits différents.
Une première approche consiste donc à fixer la structure et la spécificité des sous-réseaux avant tout apprentissage, à partir de connaissances a priori du problème à traiter. On peut aussi partir de sous-réseaux identiques au départ, ou ne différant que par un tirage au sort des conditions initiales. Pour éviter que les mêmes patterns d'entrée ne conduisent aux mêmes attracteurs, les unités des sous-réseaux différents sont reliées par des connexions inhibitrices (c'est-à-dire négatives), fixes, empêchant les cellules d'être dans le même état. En somme, en présence d'une structure biologique organisée comme le cerveau, on peut toujours se demander quelle en est la part de l'inné et de l'acquis: certaines expériences comme celle de D. Hubel et T. Wiesel sur la reconnaisance par les chatons des lignes orientées, ou quelques simulations comme celle de R. Linsker sur la structuration du cortex, tendent à montrer que la part de l'apprentissage est plus importante que celle qu'on aurait pu imaginer a priori.
6-2 EVITER LA CATASTROPHE: LES PALIMPSESTES
Considérons un réseau de Hopfield auquel on rajoute indéfiniment des patterns. Dès que leur nombre dépasse 0,14 N , le système "perd la mémoire". Aucun des patterns antérieurs n'est plus reconnu. De plus, les nouveaux patterns présentés après la catastrophe des 14% ne sont pas reconnus non plus. Un système aussi fragile ne peut être pris directement comme un modèle d'apprentissage de l'esprit humain. La première modification du modèle qui vient à l'esprit est de supposer que les intensités synaptiques ne sont pas uniformément malléables. Nous supposerons donc qu'à chaque nouvelle présentation p, une variable e (p) représente une intensité de l'apprentissage. On pourrait à ce propos parler d'attention. L'algorithme de Hebb est donc généralisé en:
![]()
![]()
La condition de stabilité du pième pattern:
![]()
![]()
se décompose suivant:
![]()
![]()
Le deuxième terme est un terme de signal, et le premier un terme de bruit, étant donné l'indépendance du pattern p par rapport aux précédents. On peut donc toujours assurer la stabilité du dernier pattern enregistré, à condition de prendre e(p) suffisamment grand pour que le signal soit plus important que le bruit. On calcule assez facilement l'amplitude de l'écart quadratique moyen du terme de bruit et on en déduit le choix de e(p). A chaque étape e(p) croît exponentiellement.
Ceci assure la stabilité des dernières séquences apprises, mais conduit à l'oubli des premières, dont la fonction de corrélation n'intervient que pour une faible part dans la matrice des connexions. Ce modèle est entièrement soluble et l'on peut réduire à chaque étape l'intensité des Tij de manière à normaliser leur amplitude.
Il est intéressant de noter qu'un modèle intuitivement plus simple et plus raisonnable en termes de biologie conduit au même comportement. Supposons simplement que les synapses sont limitées en amplitude et qu'elles sont soit positives, soit négatives. Autrement dit:
0 < Tij < A ,
ou bien -A < Tij < 0
L'apprentissage se fait à intensité constante, mais dans les limites précisées plus haut. A chaque présentation on calcule:
![]()
![]()
Si le nouveau Tij est dans les limites, il est conservé. Sinon, il prend pour valeur la limite dépassée. La figure 6.3 montre l'allure de la variation de Tij au cours d'une session d'apprentissage.
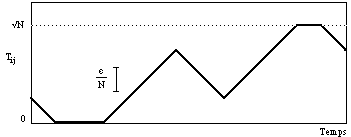
Figure 6.3
Evolution de l'intensité d'une connexion excitatrice entre 0 et la saturation au cours de l'apprentissage. (D'après J. P. Nadal, Thèse, Paris, 1987.)Les résultats suivants ont été prédits théoriquement, et vérifiés par les simulations. L'amplitude maximum A des connexions est choisie égale à pour que les résultats sur e soient indépendants de N. Si e est trop petit par rapport à , la catastrophe des 14% intervient avant que les connexions atteignent les bornes A. Par contre si e est trop grand, seul est retenu le dernier pattern présenté. On peut montrer que le meilleur choix ec pour e, de l'ordre de 3, permet de retenir les aN derniers patterns présentés avec une erreur relative maximum d'environ 0,97 (a = 0,015). Les patterns antérieurs, quant à eux, sont oubliés. Le comportement du système est analogue à la récupération des anciens parchemins par les scribes du Moyen Age: ceux-ci effaçaient les manuscrits romains pour pouvoir écrire à nouveau sur le parchemin. Ces parchemins récupérés s'appellent des palimpsestes, d'où le nom donné à l'algorithme.
La figure 6.4 montre l'évolution de a, la capacité relative du réseau en termes de patterns effectivement retenus, au fur et à mesure de la présentation des patterns; g est le rapport du nombre des patterns présentés à celui des automates. Si e est trop petit, la capacité augmente au début jusqu'à la saturation fixée à 0,14, puis décroît ensuite jusqu'à 0. Si e est supérieur à la valeur critique ec, l'augmentation de a n'atteint pas 0,14; mais par la suite, a tend vers une valeur asymptotique lorsque g augmente indéfiniment. La dépendance de la capacité asymptotique en e est représentée sur la figure 6.5.

Figure 6.4

Figure 6.5
Capacité asymptotique du réseau en fonction de l'intensité de l'apprentissage. (D'après J. P. Nadal, Thèse, Paris, 1987.)Le comportement de rappel des patterns récents et d'oubli des patterns anciens est un modèle raisonnable de la mémoire à court terme. En psychologie expérimentale, on présente des séries de mots, de figures simples ou de chiffres à un sujet et l'on observe la quantité d'objets mémorisables. Assez curieusement, quels que soient l'individu et la nature des objets, cette quantité est en moyenne de sept, avec une variabilité maximum de plus ou moins deux. Ce petit nombre est à rapprocher de la faible fraction des patterns mémorisés dans le modèle. Il est intéressant de noter que le modèle permet d'aborder une question que l'on peut se poser à propos de l'oubli : celui-ci est-il dû à une décroissance quasi automatique de l'intensité des connexions, ou au contraire aux distorsions entraînées par l'apprentissage de nouveaux objets ? Bien entendu, le modèle conclut en faveur de la deuxième hypothèse, ce que confirment des expériences récentes.
On peut se poser aussi des questions à propos de la mémoire à long terme. Notons qu'avec le même modèle que celui que nous avons décrit, si l'on choisit de "coller" la connexion Tij à la limite qu'elle atteint la première fois, on favorise au contraire la mémorisation des premiers patterns.
6-3 Reseaux asymetriques et dilution
La contrainte des liaisons symétriques, imposée par la règle de Hebb, est difficilement imaginable dans un système naturel comme le cerveau. Rappelons que l'algorithme du perceptron aboutit à une matrice de connexions asymétrique. On peut aussi partir de la règle de Hebb et "diluer" les connexions en annulant au hasard certaines d'entre elles. Cette dilution est asymétrique, la coupure d'une connexion Tij n'entraînant pas forcément la coupure de la connexion symétrique Tji. Les capacités du réseau en termes de nombre maximum d'attracteurs et de fidélité de la restauration décroissent régulièrement lorsqu'on augmente le pourcentage de liens coupés. C'est ainsi qu'avec 50% de liens, le nombre maximum d'attracteurs est de 0,09 N et la fidélité supérieure à 0,9. On peut même faire fonctionner un réseau dans la limite des fortes dilutions, telle que la connectivité k (le nombre des entrées d'un automate) soit inférieure à log(N). En utilisant une technique, dite des distances, que nous exposerons au chapitre 10, on peut même calculer théoriquement les performances de ces réseaux dilués. Pour une connectivité k, le nombre maximum des patterns mémorisables est:
m = 1 + 0,64 k (6.29)
q, la projection de l'attracteur Sa sur la référence Ss, est définie par:
![]()
![]()
Si q = 1, attracteur et référence sont confondus, et si q = 0 ils sont orthogonaux. La différence entre 1 et q est donc une indication de la distance relative entre l'attracteur et la référence. Pour le modèle très dilué, q, la projection sur la référence, vaut:
![]()
![]()
![]()
![]()
Encore une fois on trouve bien une capacité maximum proportionnelle à la connectivité des automates. Le système n'admet pas simplement un unique point fixe au voisinage de la référence : on peut montrer que si une configuration initiale est proche de la référence, sa projection moyenne sur celle-ci est donnée par l'expression ci-dessus. Par contre, deux configurations initiales proches de la référence ne convergent pas l'une vers l'autre : on démontre que leur projection moyenne tend vers une valeur proche, mais différente, de 1. Il y a donc autour de la référence, soit plusieurs points fixes, soit un cycle limite.
6-4 SEQUENCES
On se propose de construire un réseau susceptible de générer des séquences temporelles de patterns. Autrement dit, le ou les attracteurs intéressants sont des cycles limites et non des points fixes. La nature nous offre de tels exemples de comportement, qu'il s'agisse du chant des oiseaux ou des séquences de contraction de différents muscles concourant à la réalisation d'un mouvement. La difficulté que nous aurions à chanter une mélodie à l'envers est une bonne indication du fait que l'on mémorise une succession, plutôt qu'un ensemble d'états auxquels on pourrait accéder dans n'importe quel ordre.
Dans le cas de l'itération parallèle, les Tij peuvent être choisis ainsi :
![]()
![]()
L'indice t de la matrice de connexion indique qu'il s'agit d'une matrice de transition de la configuration s à la configuration s + 1.
Toutes les analyses que nous avons faites précédemment, telle celle du rapport signal sur bruit, ou bien les essais d'amélioration des performances par des techniques de type perceptron ou Widrow-Hoff, s'appliquent à ce modèle à condition de remplacer les fonctions de corrélation du type Sis Sjs par des fonctions de transition Sis+1 Sjs.
Il est plus difficile de traiter le cas des itérations séquentielles, qui est cependant plus pertinent pour les modèles biologiques. La solution proposée par P. Peretto et J.J. Niez consiste à prendre comme argument de la fonction de Heaviside une somme de deux termes :
![]()
![]()
avec
![]()
![]()
et
![]()
![]()
Le premier terme assure la stabilité des séquences et le second la transition d'une séquence à l'autre. Encore une fois, l'analyse signal/bruit montre que pendant un temps t après une transition, seule la première somme contient un terme de signal qui assure la stabilité. Après le temps t, la deuxième somme comprend elle aussi un terme de signal qui entraîne la transition vers la configuration suivante si l est plus grand que 1.
6-5 Conclusion provisoire
On a développé ces dernières années de très nombreuses variantes des systèmes à la Hopfield et la plupart des hypothèses restrictives qui donnaient au modèle sa simplicité formelle peuvent être élargies sans que le modèle perde ses propriétés. Bien entendu, ce cadre conceptuel présente quand même des limites, dont certaines peuvent être dépassées par d'autres approches que nous décrirons dans les prochains chapitres.
L'une des limites les plus graves est que ce système ne permet pas une reconnaissance invariante. Le modèle de Hopfield n'accepte que des déformations ponctuelles des patterns. Prenons le cas d'une image. Si une fraction, même importante, des pixels de l'image est modifiée, l'image est toujours reconnue. Par contre les déformations de l'image, comme la translation, la rotation, l'homothétie, etc. modifient un très grand nombre de pixels et donnent de grandes distances de Hamming par rapport à la référence. L'image déformée n'est donc plus reconnue. Bien entendu, les systèmes naturels reconnaissent les patterns déformés, et ces propriétés de reconnaissance invariante sont recherchées dans toutes les applications de traitement du signal, qu'il s'agisse de parole, d'image, etc. L'applicabilité du système de Hopfield concerne donc essentiellement des patterns d'attributs caractéristiques, bien plus que des images. Pour utiliser ces systèmes en traitement d'image, il faut disposer de modules de prétraitement qui, par exemple, recentrent l'image dans le cas de translations. Un autre prétraitement possible consiste à extraire les attributs caractéristiques (voir le paragraphe 9.2). Dans ce cas, les automates sont spécifiques de tel ou tel attribut, et codent alors la présence ou l'absence de celui-ci dans l'image.
Références
Les performances de l'algorithme optimal, dérivé de celui du perceptron, sont discutées dans un article de W. Krauth et M. Mézard "Learning Algorithms with Optimal Stability in Neural Networks", J. Phys. A: Math Gen. 20, L745 (1987).
Les méthodes algébriques sont clairement exposées avec un grand luxe d'applications dans le livre de T. Kohonen: Self-Organization and Associative Memory, Springer Series in Information Sciences, vol 8, Springer Verlag (1988). Le chapitre "Automata Networks and Artificial Intelligence" du livre collectif Automata Networks in Computer Science, édité par F. Fogelman-Soulié, Y. Robert et M. Tchuente, Manchester University Press (1987), traite des formalismes linéaires et non linéaires en donnant quelques évaluations comparatives des différents algorithmes.
Le problème de la différenciation des couches est abordé dans un article de R. Linsker "From Basic Network Principles to Neural Architecture: Emergence of Orientation Columns", Proc. Nat. Acad. Sci. U.S.A, 83, pp. 8779-8783 (1986).
Pour les palimpsestes nous nous sommes inspiré de l'article de J. Nadal, G. Toulouse, J. Changeux et S. Dehaene "Networks of Formal Neurones and Memory Palimpsests", Europhysics Letters, 1, pp. 535-542 (1986).
Les résultats sur les réseaux dilués figurent dans B. Derrida, E. Gardner et A. Zippelius "An Exactly Soluble Asymmetric Neural Network Model", Europhysics Letters, 4, p. 167 (1987).