CHAPITRE 9
Le recuit simulé
Nous allons étudier dans ce chapitre une méthode d'optimisation combinatoire, le recuit simulé. Les problèmes d'optimisation qui se posent en technologie peuvent atteindre rapidement une complexité redoutable et nécessiter des temps de calcul impressionnants, à cause de l'explosion combinatoire du nombre des solutions à envisager. Un exemple simple, celui de l'affectation, permettra de situer les difficultés.
Le problème de l'affectation
Supposons qu'une entreprise veuille répartir N tâches différentes (liées à la fabrication, à la réception de composants, à l'expédition des produits, à la comptabilité, etc.) dans N locaux d'un bâtiment. Chaque répartition présente des avantages et des inconvénients, en ce qui concerne l'adéquation entre la tâche et le local, ou bien dans les problèmes de transmission de matière ou d'information entre les locaux. Nous supposons de plus que l'on peut chiffrer, ou au moins classer, l'efficacité de chacune des répartitions, par exemple en termes de prix de revient des produits manufacturés. Le problème de l'affectation est de déterminer la répartition la plus efficace.
L'utilisation de la force brute consiste à calculer et à comparer l'efficacité des N! répartitions possibles pour déterminer la meilleure. Autrement dit, la complexité du problème, en termes du temps de calcul nécessaire pour le résoudre, croît au moins comme N!. Ces temps de calculs exponentiels, dits non polynomiaux, rendent illusoire l'utilisation d'algorithmes de "force brute" dès que le nombre des composants dépasse quelques dizaines.
Une autre approche, appelée méthode de la descente la plus rapide et dérivée de celle du gradient, moins coûteuse en temps de calcul, peut être employée. Elle consiste à partir d'une répartition initiale quelconque, et à tenter des permutations. On intervertit par exemple la localisation de deux tâches et on compare la nouvelle efficacité à l'ancienne : si l'efficacité a augmenté, la nouvelle répartition est temporairement adoptée et utilisée comme un nouveau point de départ pour un nouvel essai. Si l'efficacité diminue lors d'un essai, on revient à la configuration précédente et on essaie une autre permutation. L'algorithme est continué jusqu'à ce qu'une affectation ne semble plus susceptible d'amélioration à la suite d'un grand nombre d'essais négatifs consécutifs.
Cet algorithme fonctionne plus ou moins bien. Le cas favorable est celui pour lequel la structure de la fonction efficacité est convexe sur l'ensemble des répartitions : autrement dit lorsqu'il n'existe qu'un seul optimum global.
La difficulté peut provenir de l'existence possible de plusieurs optima locaux de répartition. Un optimum local se définit par le fait que toute permutation partielle – dans un ensemble déterminé à l'avance, par exemple celui des permutations deux à deux – fait décroître la fonction efficacité. Les valeurs des efficacités des optima locaux peuvent très bien différer les unes des autres. Or le problème posé au départ est d'obtenir la meilleure efficacité parmi toutes les répartitions possibles, donc le meilleur des optima. La méthode du gradient peut donc très bien aboutir, lorsqu'il existe plusieurs optima, à figer le système dans une configuration qui n'est pas la meilleure. Une des variantes consiste à faire plusieurs essais à partir de configurations initiales choisies arbitrairement, ou astucieusement quand on le peut, d'atteindre chaque fois l'optimum local, et puis de les comparer pour ne garder que le meilleur. Mais rien n'assure que l'un des essais ait abouti à l'optimum global, surtout s'il y a beaucoup d'optima locaux. D'où l'idée de "bien orienter" au départ le choix des configurations d'essai.
Le recuit thermique
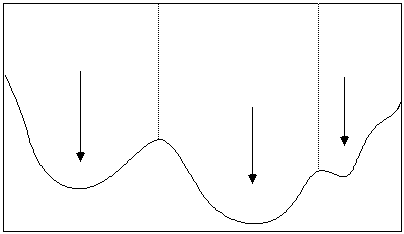
Revenons maintenant à la thermodynamique. La "recherche" par un système physique des états d'énergie les plus bas est l'analogue formel d'un processus d'optimisation combinatoire. A température nulle, le système évolue à partir d'une configuration vers la, ou les, configurations d'énergie les plus basses par une méthode de type gradient. Par conséquent, dans le cas d'un système frustré, la configuration atteinte est le plus souvent un état métastable, dont l'énergie est supérieure à celle du minimum absolu. Le système est en quelque sorte piégé dans ce minimum local (Fig. 9.1).

Figure 9.1
En revanche, à température non nulle, le caractère probabiliste des changements de configuration peut permettre au système de remonter la pente et de ressortir du bassin d'attraction d'un minimum relatif pour accéder à un autre bassin plus profond. Idéalement, pour se rapprocher du minimum, il faudrait que la température soit assez grande pour permettre au système de sauter les barrières et qu'elle soit assez faible pour qu'il soit malgré tout attiré vers le fond des vallées.
Envisageons alors une double dynamique : celle de la recherche des minima à température fixée, plus une dynamique de diminution de la température. Si l'on part d'une température élevée, toutes les configurations sont accessibles et le système n'a qu'une faible préférence pour les états de faible énergie. En diminuant progressivement la température, on permet au système de rechercher des bassins d'attraction relativement larges au début, tout en lui évitant d'être piégé par les attracteurs métastables. Le nombre des configurations accessibles dépend de la température; aux températures moyennes le système semble surtout sensible aux traits les plus grossiers du paysage dynamique. En diminuant lentement la température, on évite de piéger le système dans des vallées d'énergie élevée, pour l'envoyer vers les bassins les plus importants et les plus profonds, là où les baisses ultérieures de température le précipiteront vers les fonds.
Un tel mécanisme s'appelle un recuit, par analogie avec les cycles thermiques utilisés en métallurgie. En effet, lors du refroidissement d'un métal ou d'un alliage, on choisit la vitesse de décroissance de la température en fonction des qualités mécaniques du solide que l'on souhaite obtenir. L'acier des outils tranchants par exemple est trempé par un refroidissement rapide : cette opération donne un cristal très imparfait, dans un état métastable donc, mais très dur. Par contre, si l'on souhaite obtenir un matériau malléable et peu cassant, il faut réaliser une structure cristalline la plus parfaite possible, d'où la nécessité d'opérer des recuits à des températures intermédiaires, de manière à éliminer les défauts du cristal. Les diagrammes suivants permettent de suivre ces phénomènes dans le cas d'un ferromagnétique (Fig. 9.2).

Figure 9.2
Configurations de basse énergie d'un ferromagnétique. A gauche figure la configuration d'énergie minimum, et à droite une configuration métastable, susceptible d'évoluer à température non nulle vers la configuration de gauche.La structure homogène, à gauche de la figure 9.2, est obtenue à température nulle dans le cas d'un recuit : elle correspond bien à une configuration d'énergie minimum. La structure de droite est obtenue après une trempe. On y voit coexister des domaines d'aimantation positive et des domaines d'aimantation négative: si les domaines étaient isolés, chacun d'eux correspondrait à un minimum d'énergie. Mais les lignes de frontière ajoutent une contribution positive à l'énergie. Leur disparition nécessiterait le retournement simultané d'un nombre important de spins, donc un accroissement momentané de l'énergie du système, que la température faible rend très peu probable. Le système est bloqué dans un état métastable.
Les propriétés thermiques des verres sont très liées à l'existence de leurs multiples attracteurs. Si le verre est refroidi rapidement, la configuration des atomes est métastable; elle est obtenue pour une température relativement élevée que nous noterons Tr. Par contre si on recuit le matériau, les changements de configuration entre états métastables ont le temps de se produire et le système continue à évoluer, même pour des températures inférieures à Tr. La température de transition est donc plus faible pour les refroidissements les plus longs. Dans le cas de la silice, on peut obtenir, suivant la vitesse de refroidissement, soit une forme amorphe appelée communément silice, soit un cristal de quartz.
9-1 LE RECUIT SIMULE
L'idée du recuit simulé en optimisation combinatoire est de simuler numériquement une opération de recuit thermique. Le principe en est le suivant :
On considère un système composé de N éléments. A chaque configuration du système est associée une fonction à optimiser. Si l'on recherche la configuration qui minimise la fonction, celle-ci joue le rôle de l'énergie. Si l'on recherche au contraire un maximum, alors on prend comme énergie l'opposée de la fonction. Les configurations du système peuvent être modifiées par des changements d'états discrets des composants du système. Bien entendu, les systèmes qui nous intéressent sont ceux qui ont un grand nombre d'optima.
On part d'une configuration aléatoire (ou choisie astucieusement en fonction du problème). Au départ de l'itération, on fixe un paramètre de température en relation avec la gamme des énergies accessibles au système. On itère alors le processus suivant (dit de Metropolis ou de Monte-Carlo): on tire au sort une modification de la configuration actuelle qui change l'énergie du système d'une quantité DE. Si l'énergie diminue, on effectue le changement. Si l'énergie augmente, on effectue le changement avec une probabilité exp - DE/T. (La procédure de Monte-Carlo et celle des automates probabilistes sont équivalentes du point de vue des états stationnaires obtenus. Les automates probabilistes nécessitent un peu plus de calcul d'exponentielles et de tirage au sort, et on préfère donc Monte-Carlo dans les cas pratiques.)
L'itération se poursuit tant que l'énergie du système diminue. Lorsque l'énergie reste stationnaire, on diminue un peu la température et l'on reprend le processus Monte-Carlo de décroissance de l'énergie. On arrête lorsque les diminutions de température restent inefficaces.
Nous allons illustrer la méthode grâce à trois applications choisies dans trois domaines différents: le voyageur de commerce (paragraphe 9.1.1), le problème de la répartition (paragraphe 9.1.2) et le traitement d'image (paragraphe 9.2). La première de ces applications est classique, mais un peu académique.
9-1-1 Le voyageur de commerce
C'est le problème modèle de l'optimisation combinatoire. Des villes sont réparties sur une carte et le voyageur de commerce doit organiser un tour visitant toutes les villes une fois et une seulement, avant de revenir à son point de départ. On recherche évidemment le tour le plus court. Dans les termes généraux exposés plus haut, il s'agit d'associer à chaque ville un numéro de passage variant de 1 à N, le nombre de villes. L'énergie d'une permutation est la longueur totale du parcours ainsi déterminé.
La configuration initiale n'est pas en général prise au hasard. Une possibilité efficace consiste à partir de la première ville, à rechercher l'étape suivante parmi les villes les plus proches. On continue l'algorithme en prenant pour chaque étape la ville non encore traversée la plus proche. Après avoir atteint la dernière ville, on revient à la ville de départ.
La permutation élémentaire d'essai consiste à inverser une section du tour. On permute quatre villes à partir d'un tour déterminé suivant la figure 9.3:
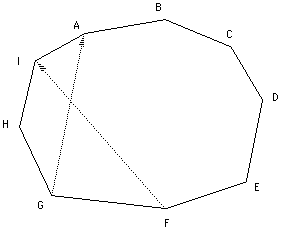
Figure 9.3
D'autres permutations, impliquant six villes par exemple, sont aussi possibles, et même plus efficaces.

Figure 9.4
La figure 9.4, tirée de l'article original de Kirkpatrick et al., représente les résultats d'une telle simulation pour un ensemble de 400 villes réparties dans un carré. Le côté du carré est pris égal à de sorte que la distance moyenne entre deux villes voisines soit en moyenne indépendante de N. Dans ce cadre, l'énergie d'un tour varie comme aN, où a est une grandeur sans dimension de l'ordre de 1. La gamme de température varie de à 1. Les quatre tours représentent une configuration stationnaire à la température indiquée et a est proportionnel à la longueur du tour. On notera aussi la répartition des villes en amas; le passage d'un amas à l'autre est stabilisé dès les hautes températures, alors que les détails les plus fins concernant le parcours des amas ne sont stabilisés qu'aux basses températures.
9-1-2 Le problème de la répartition
La conception des circuits intégrés, comme celle des circuits imprimés pose aux ingénieurs de nombreux problèmes d'optimisation combinatoire. La répartition des fonctions logiques entre circuits intégrés, le placement des circuits intégrés sur les cartes, le routage des connexions sont trois exemples parmi d'autres. Le problème de la répartition permet de bien illustrer la démarche. Dans la première phase de conception d'un ordinateur, on commence par tracer le schéma des diverses fonctions logiques nécessaires (portes logiques, bascules, compteurs, registres à décalages...) et de leurs connexions. Il s'agit ensuite, de décider quels circuits intégrés VLSI contiendront ces fonctions. Dans l'état actuel de la technique il n'est pas possible de grouper toutes les fonctions en un seul circuit intégré, qui aurait alors une trop forte probabilité de ne pas fonctionner. Il faut tenir compte de deux impératifs contradictoires, sources de frustration:
• les circuits ne doivent pas contenir trop de fonctions logiques, pour diminuer les risques de pannes;
• il faut éviter les interconnexions entre les circuits, coûteuses en termes de "pattes" et de circuiterie imprimée.
Il est donc nécessaire de répartir les fonctions logiques entre plusieurs circuits de manière à satisfaire au mieux les deux contraintes. Prenons le cas de la répartition de fonctions notées i entre deux circuits intégrés A et B. Si la fonction est implémentée sur le circuit A, la variable reliée Si prend la valeur +1, et -1 si elle est sur le circuit B. La matrice des connectivités aij indique les connexions nécessaires entre les différentes fonctions logiques. Ses éléments valent 1 si la connexion est nécessaire, et 0 si non.
On suppose que les connexions réalisées sur circuit intégré ne coûtent rien, et que seules coûtent celles établies entre les deux circuits. Le nombre de ces connexions, élément important de la fonction coût, est donné par :
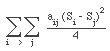
![]()
Il nous faut aussi tenir compte de l'encombrement des circuits par un terme proportionnel au carré de la différence entre les populations des deux circuits:
![]()
![]()
On choisit en général l de l'ordre de k/2, où k est la connectivité moyenne d'une fonction.
Minimiser la somme de ces deux termes revient à minimiser
![]()
![]()
La ressemblance entre cette fonction coût et la fonction énergie d'un système de spins est frappante. Les termes d'interaction sont tantôt positifs en l'absence de connexions entre i et j, favorisant alors l'implantation des deux fonctions dans des circuits distincts, tantôt négatifs, dans le cas contraire, ce qui favorise leur implantation sur le même circuit.

Figure 9.5
Les modifications élémentaires de la répartition consistent évidemment à changer une fonction de circuit en changeant le signe de Si. La dynamique du recuit simulé est donc formellement équivalente à la descente en température d'un verre de spins. La figure 9.5 montre les résultats d'une simulation numérique où environ 5 000 portes logiques sont réparties entre deux circuits intégrés. L'histogramme des solutions est donné en fonction du nombre total des pattes de sortie permettant les connexions entre les deux circuits, plus les connexions externes (200 signaux logiques arrivant ou partant de l'ensemble). On voit que la qualité des résultats est considérablement améliorée par le recuit.
En résumé, la technique du recuit simulé est une méthode très générale permettant de trouver des solutions approchées en optimisation combinatoire. Or dans la plupart des cas, la recherche du minimum absolu n'est pas requise et l'on peut se contenter d'une valeur approchée dans la mesure où l'écart entre les deux énergies est faible. L'intérêt de la méthode est sa très grande généralité, et le fait que la procédure est facilement parallélisable. Pour une application donnée, il faut essentiellement déterminer les modifications élémentaires de configurations que l'on utilisera pour les essais. Le calcul des changements d'énergie correspondants doit être simple: il ne doit faire intervenir à chaque essai qu'une faible fraction des données du problème. La difficulté principale de la méthode réside dans le choix des paliers de température. Il n'est pas toujours possible de définir un protocole à l'avance. Le plus souvent on procède de manière empirique : on regarde évoluer le système en partant des hautes températures, on repère les températures où le système n'évolue plus, on recuit longtemps à des températures légèrement supérieures avant de continuer la descente.
Les applications technologiques faisant appel à l'optimisation combinatoire sont très nombreuses. Nous avons cité plus haut la conception assistée par ordinateur, mais la technique du recuit simulé a déjà été utilisée dans des domaines aussi variés que la programmation du ramassage des ordures dans la ville de Grenoble ou la meilleure découpe des pièces d'un costume dans un coupon de tissu. De nombreuses applications de traitement du signal peuvent aussi être abordées dans cette optique. Nous développons plus bas le traitement d'image.
9-2 TRAITEMENTS D'IMAGE
Le traitement d'image est un ensemble de techniques permettant d'améliorer les images et d'en permettre l'interprétation. La première étape est la digitalisation de l'image: celle-ci est découpée en cellules élémentaires les pixels. Une image devient ainsi une matrice dont les éléments sont les intensités lumineuses en chaque pixel. Les intensités peuvent être des variables discrètes, codées suivant un certain nombre de bits: 1 (noir ou blanc), 8, 12, 16, ou bien des variables réelles, dans l'idéal. Dans le cas d'images couleurs, trois variables, une par couleur fondamentale, décrivent l'état de chaque pixel. Dans le cas du noir et blanc, une seule intensité, le niveau de gris est suffisante.
On applique ensuite à l'image digitalisée une série de transformations hiérarchisées depuis le niveau le plus bas, c'est-à-dire celui de l'image directement recueillie sur les capteurs (plaque photo, caméra de télévision, batterie de détecteurs de particules) vers le plus élevé, c'est-à-dire celui de l'interprétation de l'image en termes d'objets familiers. La reconnaissance par convergence vers un attracteur, que nous avons évoquée aux chapitres 5 et 7, ou par passage d'un pattern à travers un réseau en couches (chapitre 8), font partie des traitements de haut niveau, permettant l'interprétation de l'image. Nous parlerons dans ce chapitre de traitements de bas niveau, permettant de reconstituer l'image, ou d'en extraire des traits caractéristiques.
9-2-1 Définitions et méthodes cellulaires
La restauration d'image
Une image acquise par un système physique est souvent 1) déformée, et 2) bruitée.
1. Les déformations peuvent provenir:
• de l'optique (au sens large) du système, aberrations et diffraction;
• ou des limites de l'acuité des détecteurs, grains de la plaque photo, canaux placés devant les détecteurs de particules, électronique de la caméra de télévision.
Si la correspondance objet-image était parfaite, on pourrait découper la surface de l'objet en éléments dont chacun n'enverrait du signal que vers un seul pixel. Du fait des imperfections, chaque pixel reçoit aussi du signal parasite venu des éléments voisins.
2. Le bruit peut avoir une origine externe, électronique par exemple, mais il peut aussi être lié à la nature physique du procédé de détection. En tomographie par rayon X ou par rayons g, le coût des instruments ou le peu d'intensité des sources font que les détecteurs sont souvent utilisés à la limite de leur sensibilité, dans un régime quantique. Ce sont donc des compteurs de particules. Le flux de particules est faible donc fluctuant, et ces fluctuations donnent naissance à un bruit important.
Les techniques de restauration d'image ont pour but de reconstituer une image la plus proche possible de l'image que donnerait un système idéal, sans déformations ni bruit.
L'extraction des traits caractéristiques
Les techniques d'interprétation d'image, pour être efficaces, sont rarement appliquées au niveau des pixels d'une image, même restaurée. Le traitement passe par des étapes intermédiaires au cours desquelles certains traits caractéristiques sont reconnus. Il peut s'agir de détection de contours, de segmentations en aires homogènes en termes d'intensité ou de texture, ou bien de techniques spécifiques. En reconnaissance de caractères par exemple, on peut utiliser des techniques de squelettisation, par lesquelles les traits larges sont remplacés par des lignes minces, et compter les intersections de ces lignes avec un ensemble prédéterminé de droites.
Les traitements cellulaires par convolution
Le caractère cellulaire de l'image digitalisée invite à des traitements cellulaires. En fait les premiers traitements, au niveau le plus bas, sont de ce type.
Une manière simple de diminuer le bruit consiste à moyenner les niveaux de gris entre pixels voisins. On opère donc un produit de convolution entre l'image reçue et un opérateur de sommation sur le voisinage v de chaque pixel:
![]()
![]()
Dans cette formule l'indice 0 correspond à l'image avant traitement et l'indice 1 au résultat. Citons une autre utilisation de la convolution, la détection des contours grâce à l'opérateur laplacien:
![]()
![]()
où z est le nombre de pixels du voisinage. Dans les régions où l'intensité ne varie guère, ou bien varie de manière régulière, cet opérateur donne des valeurs de x1 faibles. Par contre, près d'un contour séparant deux parties de l'image où l'intensité varie notablement, on obtient des grandes valeurs de x1.
Plusieurs opérations simples en traitement d'image font intervenir des produits de convolution par des opérateurs locaux. On peut les comparer à une itération unique sur un réseau d'automates cellulaires. Ces opérations, comme tout un ensemble d'autres traitements cellulaires, sont simples, peuvent être effectuées en parallèle et ne nécessitent aucune connaissance préalable du sujet de l'image.
9-2-2 Traitements probabilistes
Distribution a priori
Une autre approche, d'un caractère très différent, consiste à utiliser des connaissances sur les propriétés statistiques des images pour réduire le bruit ou pour interpréter les images. On s'attend a priori à ce que l'intensité ne varie pas brusquement d'un pixel à l'autre, sauf le long de lignes continues délimitant les contours des objets. Les "bonnes" images ont toutes les chances d'être "régulières": il y a lieu de soupçonner les irrégularités d'être des défauts dus au bruit ou à certaines imperfections de l'appareillage.
L'idée consiste à traduire notre attente d'images "bien régulières" en termes de probabilité d'observation. Soit l'ensemble de toutes les images observables sur une matrice de N5N pixels:
Xp = { Xpi }
où p est l'indice de l'image et i celui du pixel. A chaque image Xp de l'ensemble on associe une probabilité qui s'exprime sous la forme suivante:
![]()
![]()
où U(x) est "l'énergie" associée à l'image Xp , et T la "température". Z le facteur de normalisation est la somme des exponentielles associées à chacune des autres configurations. Nous retrouvons là une formulation qui rappelle la mécanique statistique. C'est l'énergie qui contient donc toutes les informations statistiques représentant nos connaissances sur les images "valables". Plus l'énergie d'une configuration est élevée, moins grande est la probabilité de l'observer. Nous donnerons plus loin plusieurs expressions possibles pour cette fonction. Une propriété importante de l'énergie est son caractère de variable locale, dans la mesure où la probabilité que le pixel i prenne la valeur xi ne dépend que des valeurs des pixels voisins. Bien entendu ce voisinage peut être plus ou moins étendu. On rend compte, par exemple, de la régularité de la figure en terme de la tendance des pixels voisins à être au même niveau, par le choix d'une énergie de la forme:
![]()
![]()
où f est une fonction paire, décroissant suivant l'amplitude de la différence de niveau entre les deux pixels voisins i et j. Par analogie avec la physique décrite au chapitre 8, nous sommes tentés de dire que les pixels voisins interagissent en fonction de leur différence de niveau.
On s'attend aussi à ce que les traits caractéristiques eux-mêmes ne soient pas répartis n'importe comment. Il est donc logique de leur attribuer des probabilités d'apparition. Limitons-nous aux cas des contours (Fig. 9.6). Un contour délimite deux régions de niveaux de gris très différents.
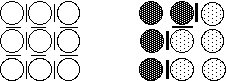
Figure 9.6
A gauche, les pixels sont représentés par des cercles et les éléments de contour, situés entre les pixels, par des traits. A droite on a représenté une configuration donnée, avec deux régions dont le niveau de gris est différent. Les traits épais représentent les éléments de contour à l'état 1, ceux à l'état 0 ne sont pas représentés.A chacune des 2N(N-1) paires i,j de pixels voisins on associe une variable binaire xcij décrivant la présence ( xcij = 1) ou l'absence ( xcij = 0) de contour. Une image est donc maintenant décrite par l'ensemble des pixels Xp et l'ensemble des contours Xc. La probabilité de l'ensemble pixels plus contours est proportionnelle à l'exponentielle d'une fonction énergie donnée par une somme de termes liés aux pixels et aux contours:
![]()
Le premier terme, dû aux interactions entre pixels, a été défini plus haut.
Le deuxième terme représente l'interaction entre les pixels voisins et la variable de contour. Si la différence de niveau est grande elle favorise l'état xc = 1 . Sinon c'est l'état xc = 0 qui correspond à l'énergie la plus basse.
Le troisième terme correspond aux interactions entre variables de contours voisines. Les situations où les contours se prolongent sont favorisées par rapport à la jonction en T ou aux croisements a priori peu probables (Fig. 9.7).
![]()
Figure 9.7
Distribution a posteriori
En traitement d'image on s'intéresse à la distribution a posteriori, c'est-à-dire à la probabilité conditionnelle des images corrigées {Xpi}, compte tenu de l'image déformée observée {Yi}.
Py (x) = P(XP = x | Y = y) (9.9)
Autrement dit, il faut combiner l'information sur les propriétés statistiques des images, contenue dans le choix de la fonction énergie, avec l'information obtenue à partir de l'image observée. La méthode la plus simple pour obtenir la distribution a posteriori consiste à rajouter à l'énergie un terme proportionnel à la distance de Hamming entre les deux images :
![]()
![]()
La distribution a posteriori est alors donnée par:
![]()
![]()
Utilisation du recuit simulé
En fait, le problème de la restauration d'image est de proposer, à partir de l'image observée, l'image restaurée la plus probable, c'est-à-dire compte tenu de l'expression ci-dessus, celle qui minimise l'énergie Uy(x). Une technique de recuit simulé s'impose donc. On part d'une configuration initiale qui est celle de l'image observée, sans contours, et l'on modifie les variables pixels et contours par des itérations successives suivant une règle de Monte-Carlo. Les variations d'énergie sont calculées d'après l'expression de Uy(x). La température décroît régulièrement jusqu'à ce que l'image restaurée soit satisfaisante. Bien entendu, la partie la plus délicate est le choix des différents paramètres définissant la fonction énergie, de même que le plan de décroissance de la température. La figure 9.8, tirée d'un article de S. Geman et D. Geman montre le résultat de la méthode dans un cas très simple.
L'utilisation du recuit simulé est une approche très prometteuse pour le traitement d'image de tomographie ou d'images satellites. Les difficultés actuelles concernent le choix automatique des nombreux paramètres définissant la fonction énergie, et bien sûr le volume des calculs, que des processeurs parallèles permettraient d'effectuer plus rapidement.

Figure originale Figure bruitée

Figure restaurée sans Figure restaurée en prenant
tenir compte des contours les contours en compte
Figure 9.8 Restauration d'image et tracé automatique de contours par recuit simulé (d'après S. Geman et D. Geman, "Bayesian image analysis", in Disordered Systems and Biological Organization, E. Bienenstock, F. Fogelman-Soulié et G. Weisbuch eds., NATO ASI Proceedings, F20, Springer 1986) .
Le lien entre systèmes magnétiques à température finie, automates probabilistes et recuit simulé est particulièrement clair dans les exemples de répartition de fonctions logiques entre circuits intégrés, et de restauration d'image. Dans ces deux cas, l'énergie apparaît sous la forme d'une somme d'interactions entre les composants, et le processus de mise à jour des variables est celui d'une itération séquentielle aléatoire d'automates probabilistes. Ce lien est moins clair dans d'autres problèmes d'optimisation combinatoire, comme celui du voyageur de commerce; dans ce cas il se réduit à l'utilisation du recuit simulé. Chacun des trois domaines a bénéficié d'apports des deux autres:
• Les méthodes de calcul de la mécanique statistique, champ moyen et méthode des répliques, viennent des sytèmes magnétiques.
• Les méthodes numériques de Monte-Carlo sont en fait des itérations aléatoires d'automates probabilistes.
• Enfin, certains algorithmes classiques de l'optimisation combinatoire ont été utilisés dans la recherche des états d'énergie minimum des verres de spins (algorithme du postier chinois par exemple).
Références
L'article original de S. Kirkpatrick, C. Gelatt et M. Vecchi, "Optimization by Simulated Annealing", Science, 220 (1983), pp. 671-680, est tout à fait lisible.
Une bonne référence sur le voyageur de commerce est le livre collectif The Traveling Salesman Problem, édité par E. Lawler, J. Lenstra, A. Rinnooy Kan et D. Shmoys, publié par John Wiley and Sons (1985).
La référence classique sur le traitement d'image est le livre de R. Duda et P. Hart, Pattern Classification and Scene Analysis, Wiley-Interscience (1973). Le paragraphe 9.2.2 sur les traitements probabilistes est directement tiré de l'article de S. German et D. German, "Bayesian image analysis", in Disordered Systems and Biological Organization, E. Bienenstock, F. Fogelman-Soutié et G. Weisbuch eds., NATO ASI Proceedings, F20, Springer (1986).
Le livre de M. Mézard, G. Parisi et M. Virasoro Spin Glass Theory and Beyond, World Scientific (1987), illustre bien les connexions entre les trois domaines: thermodynamique, optimisation et réseaux de neurones.