Bernard Krauth 2012
From Werner KRAUTH
E. P. Bernard, W. Krauth Addendum to Event-chain Monte Carlo algorithms for hard-sphere systems Phys. Rev. E 86, 017701 (2012)
Contents |
Paper
Abstract: We extend the event-chain Monte Carlo algorithm from hard-sphere interactions to the micro- canonical ensemble (constant potential energy) for general potentials. This event-driven Monte Carlo algorithm is non-local, rejection-free, and allows for the breaking of detailed balance. The algorithm uses a discretized potential, but its running speed is asymptotically independent of the discretization. We implement the algorithm for the cut-off linear potential, and discuss its possible implementation directly in the continuum limit.
Electronic version (from arXiv)
Published version (subscription required)
Note
In a subsequent 2014 paper in Journal of Chemical Physics, with Manon Michel and Sebastian Kapfer entitled Generalized event-chain Monte Carlo: Constructing rejection-free global-balance algorithms from infinitesimal steps, we presented an improved event-chain algorithm for continuous potentials that really works in the continuum, and does not require the restriction to the micro-canonical ensemble.
Illustration
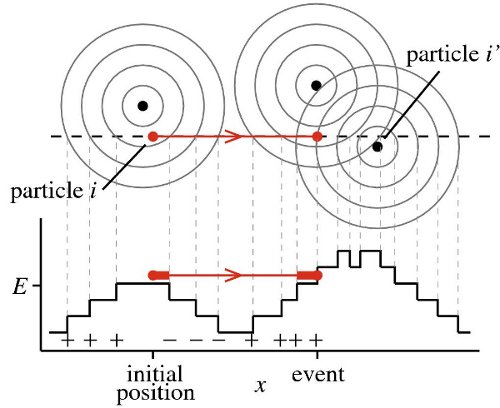
Event-driven Monte Carlo displacement for four particles interacting via the Tower-of-Hanoi potential. Particle i moves from its initial configuration until its collisionevent with particle i´ (potential of Eq. (1) with E = 1/4 and
E = 3/4). Only displacements at energy E are discounted
from ℓ.
Implementations
Naive Python implementation
Here is a naive Python implementation of the event-driven Monte Carlo algorithm for the stepped Hanoi-tower potential. In this implementation, we first choose a particle (called "next_particle"), and translate the entire configuration such that next_particle comes to lie at (0,0). We then try to move it in the positive x direction, computing all the possible events on the line. Each event is characterized by the x position, the signature (=/- 1) and the particle responsible for it. Events are listed in list "next_events", then sorted. Going through this list we find the event which would move the energy beyond the current value.
#!/usr/bin/python
###========+=========+=========+=========+=========+=========+=========+=
## PROGRAM : event_stepped.py
## TYPE : Python script (python 2.7)
## PURPOSE : Event-chain simulation for N particles with a stepped
## potential in a square with periodic boundary conditions.
## COMMENT : L is a list of tuples
## VERSION : 29 Nov 2011
##========+=========+=========+=========+=========+=========+=========+
from random import uniform, randint, choice, seed
import math, pylab, sys, cPickle
Energy_check_iteration = 0
def translate(x,del_x):
x_trans=((x[0]-del_x[0])%box,((x[1]-del_x[1])%box))
return x_trans
def dist(x,y):
"""periodic distance between two two-dimensional points x and y"""
d_x= abs(x[0]-y[0])%box
d_x = min(d_x,box-d_x)
d_y= abs(x[1]-y[1])%box
d_y = min(d_y,box-d_y)
return math.sqrt(d_x**2 + d_y**2)
def potential(r,k):
"""particles have a radius of interaction sigma = 1. The interaction passes
in k steps from 1 (at r=1) to zero (at r=0). Conditions on interaction range
and box size
2 sigma < box
assure that two particles interact only through one path."""
if r > sigma:
pot = 0
else:
pot = k - int(r*k)
return pot
def Energy_calc(L):
"""elementary calculation of the energy for the configuration in list L """
Energy=0
for k in range(1,N):
for l in range(k):
Energy += potential(dist(L[k],L[l]),Nstep)
return Energy
def x_image_calc(x_vec):
"""x_vec describes the position of a particle inside the box. This
function computes the closest "image" of x_vec to the point (0,0). The
conditions on the box size box, the interaction range sigma and the
length of the interval l_max
l_max < box/2.
l_max + 2 sigma < box
assure that the image position is closest to the entire interval [(0,0)
(l_max,0)."""
x = x_vec[0]
y = x_vec[1]
if x < 0 or x > box or y < 0 or y > box: print 'error',sys.exit()
if x < box/2: x_image = x
else : x_image = x - box
if y < box/2: y_image = y
else: y_image = y-box
return (x_image, y_image)
def x_intersection(x_vec,d):
"""compute intersections between the circle of radius d, with center x_vec, and the x-axis.
We suppose that abs(x_vec[1]) < d, so that two such intersections exist."""
del_x= math.sqrt(d**2 - x_vec[1]**2)
return (x_vec[0]-del_x, x_vec[0]+del_x)
def Flip_conf(L,rot):
L_flip=[]
for (a,b) in L:
if rot == 1: L_flip.append((box - b,a))
else: L_flip.append((b,box - a))
return L_flip,-rot
def Energy_check(L,message_string):
global Energy_check_iteration,Energy_level
Energy_check_iteration += 1
a= Energy_calc(L)
if a == Energy_level:
return ('OK',a,Energy_check_iteration)
else:
return ('Error',a,Energy_level,Energy_check_iteration)
#==============================================================================================
#=========================== main program starts here =========================================
#==============================================================================================
#
seed('Test')
Event_eps=1.e-12 # disallow events within too close bounds.
Zero = 0.0
One = 1.0
box = 4.0
sigma = 1.0
N = 4
Nstep = 100
data = []
while True:
L = [(uniform(0.,box),uniform(0.,box)) for k in range(N)]
Energy_level_initial = Energy_calc(L)
if Energy_level_initial == 90: break
Energy_level = Energy_level_initial
rot = 1
ltilde = 0.03
for iter in xrange(100000):
L_save = L[:]
if iter % 10000 ==0: print iter
i=randint(0,N-1)
j=(i+randint(1,N-1))%N
data.append(dist(L[i],L[j]))
if randint(0,1) < 1: L,rot = Flip_conf(L,rot)
#
# this iteration will be used up when the Zero_distance_to_go falls to zero
#
Zero_distance_to_go = ltilde
next_particle = choice(L)
while Zero_distance_to_go > Zero:
Total_distance_to_go = min(box/2,box/2-sigma)*.3971
L.remove(next_particle)
L = [translate(x,next_particle) for x in L]
next_events = []
Current_position = Zero
for x in L:
x_image = x_image_calc(x)
for k in range(1,Nstep+1):
distance = k/float(Nstep)
if abs(x_image[1]) < distance:
x_dummy = x_intersection(x_image,distance)
if x_dummy[0] > Event_eps and x_dummy[0] < Total_distance_to_go:
next_events.append((x_dummy[0],1,x))
if x_dummy[1] > Event_eps and x_dummy[1] < Total_distance_to_go:
next_events.append((x_dummy[1],-1,x))
next_events.append((float("inf"),0,(float("inf"),Zero))) # Final event, at infinity
next_events.sort(reverse=True)
while min(Total_distance_to_go,Zero_distance_to_go) > Zero:
#
# this single-particle loop leads to either:
# 1. A particle collision
# 2. Zero_distance_to_go = 0
# 3. Total_distance_to_go = 0
#
next_position,next_energy_level,next_particle = next_events.pop()
distance_to_next_event = next_position - Current_position
if Energy_level < Energy_level_initial:
if Total_distance_to_go < distance_to_next_event:
Current_position += Total_distance_to_go
next_particle = (Current_position,Zero)
L.append(next_particle)
break
else: # go to event, but energy will not be too high: remain in loop of one particle...
Current_position += distance_to_next_event
Energy_level += next_energy_level
Total_distance_to_go -= distance_to_next_event
else: # Energy_level == Energy_level_intial
min_dist= min(Total_distance_to_go, Zero_distance_to_go)
if min_dist < distance_to_next_event:
Current_position += min_dist
Total_distance_to_go -= min_dist
Zero_distance_to_go -= min_dist
next_particle = (Current_position,Zero)
L.append(next_particle)
break # we can break here, because either Tdtg or Zdtg are zero, but next particle is old one
else:
#
# We go to a new event.
#
Current_position += distance_to_next_event
Total_distance_to_go -= distance_to_next_event
Zero_distance_to_go -= distance_to_next_event
if next_energy_level < 0: # we went to event, but energy is not too high, remain in loop of one particle
Energy_level += next_energy_level
else: # exit one-particle loop: use the next particle as given in the list...
L.append((Current_position,Zero))
break
if Energy_calc(L) != 90:
L = L_save[:]
print 'error at ', iter
f=open("event_stepped_13.data","w")
cPickle.dump(data,f)
f.close()
pylab.hist(data,bins=40,normed=True)
pylab.title("Event_stepped ltilde= "+str(ltilde)+" N= "+str(N)+" Energy = "+str(Energy_level))
pylab.savefig('Event_stepped.png')
pylab.show()
Comparison with direct-sampling algorithm
Here is, a completely trivial constant-energy direct-sampling algorithm for four particles in a periodic square box. In the below figure, we compare its integrated pair-correlation function with the one of the event-driven algorithm for k = 100 (delta_E = 0.01). Outputs are truly the same.
###========+=========+=========+=========+=========+=========+=========+=
## PROGRAM : direct_stepped.py
## TYPE : Python script (python 2.7)
## PURPOSE : Direct sampling simulation for N particles with a stepped
## potential in a square with periodic boundary conditions.
## COMMENT : L is a list of tuples
##========+=========+=========+=========+=========+=========+=========+
from random import uniform, randint
import math, pylab, cPickle
box=4.
N=4
def dist(x,y):
"""periodic distance between two two-dimensional points x and y"""
d_x= abs(x[0]-y[0])%box
d_x = min(d_x,box-d_x)
d_y= abs(x[1]-y[1])%box
d_y = min(d_y,box-d_y)
return math.sqrt(d_x**2 + d_y**2)
def potential(r,k):
"""particles have a radius of interaction sigma = 1. The interaction passes
in k steps from 1 (at r=1) to zero (at r=0). Conditions on interaction range
and box size
2 sigma < box
assure that two particles interact only through one path."""
if r > sigma:
pot = 0
else:
pot = k - int(r*k)
return pot
def Energy_calc(L):
"""elementary calculation of the energy for the configuration in list L """
Energy = 0
for k in range(1,N):
for l in range(k):
Energy += potential(dist(L[k],L[l]),Nstep)
return Energy
sigma= 1.0
Nstep = 100
energy=0.904
Energy_hist = int(energy*Nstep+0.5)
data=[]
for iter in xrange(1000000):
L = [(uniform(0.,box),uniform(0.,box)) for k in range(N)]
Energy=Energy_calc(L)
if Energy == Energy_hist:
i=randint(0,N-1)
j=(i+randint(1,N-1))%N
data.append(dist(L[i],L[j]))
f = open('Direct_stepped'+str(Nstep)+'.data',"w")
cPickle.dump(data,f)
f.close()
pylab.hist(data,bins=40,normed=True,facecolor='green')
pylab.title("Direct_stepped N= "+str(N)+", k = "+str(Nstep)+" Energy = "+str(Energy_hist/float(Nstep)))
pylab.savefig('Direct_stepped'+str(Nstep)+'.png')
pylab.show()
Here is a comparison, at energy 0.904 of the integrated pair distribution function between the Event-driven MC algorithm and the trivial direct-sampling method. There is no doubt that the distributions are the same.
Sophisticated Python implementation
As discussed in our paper, the event-drivent algorithm can be implemented for arbitrarily small values of Delta_E with a complexity O(1). This means that the running time of the algorithm is independent of the discretization.
The below program implements the corresponding algorithm in basic Python. Running times were about 6 minutes, for a 100-step discretization just as for a million steps. A more detailed description of this program has unfortunately not been published yet.
Here is a comparison, at energy 0.900 of the integrated pair distribution function between the Event-driven MC algorithm with different values of the discretization. Running times were roughly the same although the Hanoi potential was put together from 10^6 little plates.
###========+=========+=========+=========+=========+=========+=========+=
## PROGRAM : event_stepped_cont.py
## TYPE : Python script (python 2.7)
## PURPOSE : Improved event-chain simulation for N particles with a stepped
## potential in a square with periodic boundary conditions. The program
## keeps track of the continuous energy, as well as of the discrete one.
## Running speed is roughly independent of the parameter N_step, which
## governs the discretization of the potential
## COMMENT : L is a list of tuples
## VERSION : 08 Jan 2012
##========+=========+=========+=========+=========+=========+=========+
from random import uniform, randint, choice, seed
import math, pylab, sys, cPickle,scipy.optimize
def translate(L,a):
"""Translate configuration with respect to the vector a"""
L_trans=[((b[0] - a[0])%box,((b[1] - a[1])%box)) for b in L]
return L_trans
def dist(x,y):
"""periodic distance between two two-dimensional points x and y"""
d_x= abs(x[0]-y[0])%box
d_x = min(d_x,box-d_x)
d_y= abs(x[1]-y[1])%box
d_y = min(d_y,box-d_y)
return math.sqrt(d_x**2 + d_y**2)
def potential(r):
"""particles have a radius of interaction sigma = 1.
The interaction passes in N_steps steps from 1 (at r=1) to zero (at r=0).
Conditions on interaction range and box size
2 sigma < box
assure that two particles interact only through one path."""
if r > One:
pot = 0
elif continuous == False:
pot = N_step - int(r*N_step)
else:
pot = One - r
return pot
def Energy(x,L,E_zero):
"""energy of configuration L + [(x,Zero)], subtract zero energy"""
E = - E_zero
L_dummy = L + [(x,Zero)]
for k in range(1,len(L_dummy)):
for l in range(k):
E += potential(dist(L_dummy[k],L_dummy[l]))
return E
def deriv_potential(a,x):
"""derivative of the uncropped continuum potential, with respect
to x."""
return (a[0]-x)/dist(a,(x,Zero))
def Energy_deriv(x,L_part):
"""Derivative of the uncropped energy for particles in list L_part
with respect to (x,Zero). L_part contains interacting particles only"""
Deriv = 0
for a in L_part:
Deriv += deriv_potential(a,x)
return Deriv
def x_image_calc(x_vec):
"""x_vec describes the position of a particle inside the box. This
function computes the closest "image" of x_vec to the point (0,0). The
conditions on the box size box, the interaction range sigma and the
length of the interval l_max
l_max < box/2.
l_max + 2 sigma < box
assure that the image position is closest to the entire interval [(0,0)
(l_max,0)."""
x = x_vec[0]
y = x_vec[1]
if x < 0 or x > box or y < 0 or y > box: print 'error',sys.exit()
if x < box/2: x_image = x
else : x_image = x - box
if y < box/2: y_image = y
else: y_image = y-box
return (x_image, y_image)
def x_intersection(x_vec,d):
"""compute intersections between the circle of radius d, with center x_vec, and the x-axis.
We suppose that abs(x_vec[1]) < d, so that two such intersections exist."""
del_x= math.sqrt(d**2 - x_vec[1]**2)
return (x_vec[0]-del_x, x_vec[0]+del_x)
def Flip_conf(L,rot):
L_flip=[]
for (a,b) in L:
if rot == 1: L_flip.append((box - b,a))
else: L_flip.append((b,box - a))
return L_flip,-rot
def L_part_comp(x,L):
"""compute the partial list of particles \in L which contribute to the
potential at (x,Zero)"""
L_part=[]
for a in L:
if (dist(a,(x,Zero)) < One): L_part.append(x_image_calc(a))
return L_part
def next_event_stepped(x,L):
"""Compute the next event, in the +x direction, for the configuration
L+[(x,0)], using the stepped energy."""
intersections=[(float("inf"),1,1)]
for a in L:
b = x_image_calc(a)
if abs(b[1]) < One:
if b[0] > x:
dist_dummy = min(int((dist(b,(x,0)) - Event_eps)*N_step)/float(N_step),One)
if dist_dummy < abs(b[1]): dist_dummy += 1./N_step
else:
dist_dummy = min(int((dist(b,(x,0.)) + Event_eps)*N_step+1)/float(N_step),One)
a_dummy = x_intersection(b,dist_dummy)
if a_dummy[0]%box > x: intersections.append((a_dummy[0]%box, 1,a))
if a_dummy[1]%box > x: intersections.append((a_dummy[1]%box,-1,a))
intersections.sort()
next_event = intersections.pop(0)
return next_event
def next_event_continuous(L,Max_distance,E_zero):
"""Compute the next event, in the +x direction, for the configuration
L+[(x=0,0)], using the continuous energy"""
intersections=[Zero]
for a in L:
b = x_image_calc(a)
if abs(b[1]) < One:
a_dummy = x_intersection(b,One)
if a_dummy[0]%box < Max_distance: intersections.append(a_dummy[0]%box)
if a_dummy[1]%box < Max_distance: intersections.append(a_dummy[1]%box)
intersections.sort()
intersections.append(Max_distance)
intervals = []
#
# here, we characterize the intervals with differentiable potent.
#
lower_bound = intersections.pop(0)
while intersections != []:
upper_bound = intersections.pop(0)
#
# here we define the interval and the contributing particles,
#
interval = [lower_bound,upper_bound]
midpoint = (lower_bound + upper_bound)/Two
lower_bound = upper_bound
L_part = L_part_comp(midpoint,L)
intervals.append((tuple(interval),L_part[:]))
x_zero = Max_distance
collision = False
for obb in intervals:
x_0 = obb[0][0]; x_1 = obb[0][1]
E_0 = Energy(x_0,L,E_zero); E_1 = Energy(x_1,L,E_zero)
E_deriv_0 = Energy_deriv(x_0,obb[1])
E_deriv_1 = Energy_deriv(x_1,obb[1])
if E_deriv_0 * E_deriv_1 > 0 and E_0 * E_1 < 0:
x_zero_test = scipy.optimize.bisect(Energy,x_0,x_1,args=(L,E_zero))
if Energy_deriv(x_zero_test,obb[1]) > Zero:
collision = True
x_zero = x_zero_test
break
elif E_deriv_0 * E_deriv_1 < 0 and min(E_0, E_1) < 0:
x_max = scipy.optimize.bisect \
(Energy_deriv,x_0,x_1,args=obb[1])
E_max = Energy(x_max,L,E_zero)
if E_max > 0 and E_0 < 0:
x_zero_test = scipy.optimize.bisect \
(Energy,x_0,x_max,args=(L,E_zero))
if Energy_deriv(x_zero_test,obb[1]) > Zero:
collision = True
x_zero = x_zero_test
break
elif E_max > 0 and E_0 > 0:
x_zero_test = scipy.optimize.bisect \
(Energy,x_max,x_1,args=(L,E_zero))
if Energy_deriv(x_zero_test,obb[1]) > Zero:
collision = True
x_zero = x_zero_test
break
return x_zero, collision, obb[1]
#==============================================================================================
#=========================== main program starts here =========================================
#==============================================================================================
#
seed('Felix')
Event_eps = 1.e-12 # disallow events within too close bounds.
Zero = 0.0
One = 1.0
Two = 2.0
box = 4.0
sigma = 1.0
N = 4
N_step = 1000000
E_zero = 0.9
data = []
continuous = False
while True:
L = [(uniform(0.,box),uniform(0.,box)) for k in range(N)]
a = choice(L)
L.remove(a)
L = translate(L,a)
Energy_level_initial = Energy(Zero,L,0)
L += [(Zero,Zero)]
if Energy_level_initial == int(E_zero*N_step): break
Energy_level = Energy_level_initial
rot = 1
ltilde = 3.0/float(N_step)
for iter in xrange(200000):
if iter%1000 ==0: print iter, 'iter'
i=randint(0,N-1)
j=(i+randint(1,N-1))%N
data.append(dist(L[i],L[j]))
if randint(0,1) < 1: L,rot = Flip_conf(L,rot)
Zero_distance_to_go = ltilde
next_particle = choice(L)
#
# this iteration will be used up when the Zero_distance_to_go falls to zero
#
while Zero_distance_to_go > Zero:
Total_distance_to_go = min(box/2,box/2-sigma)*.3971
L.remove(next_particle)
L = translate(L,next_particle)
Current_position = Zero
while min(Total_distance_to_go,Zero_distance_to_go) > Zero:
if Energy_level < int(N_step*E_zero - 6):
L = translate(L,(Current_position,Zero))
Current_position = Zero
continuous = True
x_zero, collision, L_part = next_event_continuous(L,Total_distance_to_go,E_zero-6./N_step)
Current_position = x_zero
Total_distance_to_go -= x_zero
continuous = False
Energy_level = Energy(Current_position,L,0)
#
# this single-particle loop leads to either:
# 1. A particle collision
# 2. Zero_distance_to_go = 0
# 3. Total_distance_to_go = 0
#
next_position,next_energy_level,next_particle = next_event_stepped(Current_position,L)
distance_to_next_event = next_position - Current_position
if Energy_level < Energy_level_initial:
if Total_distance_to_go < distance_to_next_event:
Current_position += Total_distance_to_go
next_particle = (Current_position,Zero)
L.append(next_particle)
break
else: # go to event, but energy will not be too high: remain in loop of one particle...
Current_position += distance_to_next_event
Energy_level += next_energy_level
Total_distance_to_go -= distance_to_next_event
else: # Energy_level == Energy_level_intial
min_dist= min(Total_distance_to_go, Zero_distance_to_go)
if min_dist < distance_to_next_event:
Current_position += min_dist
Total_distance_to_go -= min_dist
Zero_distance_to_go -= min_dist
next_particle = (Current_position,Zero)
L.append(next_particle)
break # Tdtg or Zdtg are zero, but next particle is old one
else:
#
# New event.
#
Current_position += distance_to_next_event
Total_distance_to_go -= distance_to_next_event
Zero_distance_to_go -= distance_to_next_event
if next_energy_level < 0: # new event, but energy not too high, remain in inner loop
Energy_level += next_energy_level
else: # exit one-particle loop: use the next particle as given in the list...
L.append((Current_position,Zero))
break
f=open("event_stepped"+str(N_step)+".data","w")
cPickle.dump(data,f)
f.close()
pylab.hist(data,bins=40,normed=True)
pylab.title("Event_stepped ltilde= "+str(ltilde)+" N= "+str(N)+" Energy = "+str(Energy_level))
pylab.savefig('Event_stepped.png')
pylab.show()