Kapfer Krauth 2016
From Werner KRAUTH
S. C. Kapfer, W. Krauth Cell-veto Monte Carlo algorithm for long-range systems Physical Review E 94, 031302(R) (2016)
Paper
Abstract We present a rigorous efficient event-chain Monte Carlo algorithm for long-range interacting particle systems. Using a cell-veto scheme within the factorized Metropolis algorithm, we compute each single-particle move with a fixed number of operations. For slowly decaying potentials such as Coulomb interactions, screening line charges allow us to take into account periodic boundary conditions. We discuss the performance of the cell-veto Monte Carlo algorithm for general inverse-power-law potentials, and illustrate how it provides a new outlook on one of the prominent bottlenecks in large-scale atomistic Monte Carlo simulations.
DOI: 10.1103/PhysRevE.94.031302
Electronic version (from arXiv, including supplemental material in one pdf file)
Journal version (subscription required)
Supplemental material (subscription required)
Open-access repository of program(s) on github
Illustration
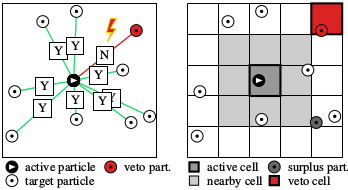
The cell-veto algorithm is an application of the event-chain paradigm that was developed in 2009, with E. P. Bernard and D. B. Wilson, and much extended together with M. Michel and S. C. Kapfer, where we introduced the factorized Metropolis algorithm. In this algorithm, unlike in 99.9% of all simulation algorithms (Monte Carlo or Molecular dynamics), one does not compute the system energy in order to decide on a change of the physical system, but rather looks at all the interactions separately. So, if a particle a (the active particle) wants to move, it has to ask all its partners t_1, t_2, .... (the target particles). If there is only a single veto, the move is rejected. In the cell-veto algorithm (see the right side of the figure), the identification of the rejecting particle is preceeded by that of a veto cell. The advantage of this is that cell vetos can be identified immediately (in a constant number of operations, that is, in O(1)), and then instantly confirmed or infirmed on the particle level.Python implementation
The paper contains a Python demo implementation of the cell-veto algorithm (that is also available on github).
import math, random, sys
import numpy as np
def norm (x, y):
"""norm of a two-dimensional vector"""
return (x*x + y*y) ** 0.5
def dist (a, b):
"""periodic distance between two two-dimensional points a and b"""
delta_x = (a[0] - b[0] + 2.5) % 1.0 - 0.5
delta_y = (a[1] - b[1] + 2.5) % 1.0 - 0.5
return norm (delta_x, delta_y)
def random_exponential (rate):
"""sample an exponential random number with given rate parameter"""
return -math.log (random.uniform (0.0, 1.0)) / rate
def pair_event_rate (delta_x, delta_y):
"""compute the particle event rate for the 1/r potential in 2D (lattice-screened version)"""
q = 0.0
for ky in range (-k_max, k_max + 1):
for kx in range (-k_max, k_max + 1):
q += (delta_x + kx) / norm (delta_x + kx, delta_y + ky) ** 3
q += 1.0 / norm (delta_x + k_max + 0.5, delta_y + ky)
q -= 1.0 / norm (delta_x - k_max - 0.5, delta_y + ky)
return max (0.0, q)
def translated_cell (target_cell, active_cell):
"""translate target_cell with respect to active_cell"""
kt_y = target_cell // L
kt_x = target_cell % L
ka_y = active_cell // L
ka_x = active_cell % L
del_x = (kt_x + ka_x) % L
del_y = (kt_y + ka_y) % L
return del_x + L*del_y
def cell_containing (a):
"""return the index of the cell which contains the point a"""
k_x = int (a[0] * L)
k_y = int (a[1] * L)
return k_x + L*k_y
def walker_setup (pi):
"""compute the lookup table for Walker's algorithm"""
N_walker = len(pi)
walker_mean = sum(a[0] for a in pi) / float(N_walker)
long_s = []
short_s = []
for p in pi:
if p[0] > walker_mean:
long_s.append (p[:])
else:
short_s.append (p[:])
walker_table = []
for k in range(N_walker - 1):
e_plus = long_s.pop()
e_minus = short_s.pop()
walker_table.append((e_minus[0], e_minus[1], e_plus[1]))
e_plus[0] = e_plus[0] - (walker_mean - e_minus[0])
if e_plus[0] < walker_mean:
short_s.append(e_plus)
else:
long_s.append(e_plus)
if long_s != []:
walker_table.append((long_s[0][0], long_s[0][1], long_s[0][1]))
else:
walker_table.append((short_s[0][0], short_s[0][1], short_s[0][1]))
return N_walker, walker_mean, walker_table
def sample_cell_veto (active_cell):
"""determine the cell which raised the cell veto"""
# first sample the distance vector using Walker's algorithm
i = random.randint (0, N_walker - 1)
Upsilon = random.uniform (0.0, walker_mean)
if Upsilon < walker_table[i][0]:
veto_offset = walker_table[i][1]
else:
veto_offset = walker_table[i][2]
# translate with respect to active cell
veto_rate = Q_cell[veto_offset][0]
vetoing_cell = translated_cell (veto_offset, active_cell)
return vetoing_cell, veto_rate
N = 40
k_max = 3 # extension of periodic images.
chain_ell = 0.18 # displacement during one chain
L = 10 # number of cells along each dimension
density = N / 1.
cell_side = 1.0 / L
# precompute the cell-veto rates
cell_boundary = []
cb_discret = 10 # going around the boundary of a cell (naive)
for i in range (cb_discret):
x = i / float (cb_discret)
cell_boundary += [(x*cell_side, 0.0), (cell_side, x*cell_side),
(cell_side - x*cell_side, cell_side),
(0.0, cell_side - x*cell_side)]
excluded_cells = [ del_x + L*del_y for del_x in (0, 1, L-1) \
for del_y in (0, 1, L-1) ]
Q_cell = []
for del_y in xrange (L):
for del_x in xrange (L):
k = del_x + L*del_y
Q = 0.0
# "nearby" cells have no cell vetos
if k not in excluded_cells:
# scan the cell boundaries of both active and target cells
# to find the maximum of event rate
for delta_a in cell_boundary:
for delta_t in cell_boundary:
delta_x = del_x*cell_side + delta_t[0] - delta_a[0]
delta_y = del_y*cell_side + delta_t[1] - delta_a[1]
Q = max (Q, pair_event_rate (delta_x, delta_y))
Q_cell.append ([Q, k])
Q_tot = sum (a[0] for a in Q_cell)
N_walker, walker_mean, walker_table = walker_setup (Q_cell)
# histogram for computing g(r)
hbins = 50
histo = np.zeros (hbins)
histo_binwid = .5 / hbins
hsamples = 0
# random initial configuration
particles = [ (random.uniform (0.0, 1.0), random.uniform (0.0, 1.0))
for _ in xrange (N) ]
for iter in xrange (250000):
if iter % 100 == 0:
print iter
# possibly exchange x and y coordinates for ergodicity
if random.randint(0,1) == 1:
particles = [ (y,x) for (x,y) in particles ]
# pick active particle for first move
active_particle = random.choice (particles)
particles.remove (active_particle)
active_cell = cell_containing (active_particle)
# put particles into cells
surplus = []
cell_occupant = [ None ] * L * L
for part in particles:
k = cell_containing (part)
if cell_occupant[k] is None:
cell_occupant[k] = part
else:
surplus.append (part)
# run one event chain
distance_to_go = chain_ell
while distance_to_go > 0.0:
planned_event_type = 'end-of-chain'
planned_displacement = distance_to_go
target_particle = None
target_cell = None
active_cell_limit = cell_side * (active_cell % L + 1)
if active_cell_limit - active_particle[0] <= planned_displacement:
planned_event_type = 'active-cell-change'
planned_displacement = active_cell_limit - active_particle[0]
delta_s = random_exponential (Q_tot)
while delta_s < planned_displacement:
vetoing_cell, veto_rate = sample_cell_veto (active_cell)
part = cell_occupant[vetoing_cell]
if part is not None:
Ratio = pair_event_rate (part[0] - active_particle[0] - delta_s, \
part[1] - active_particle[1]) \
/ veto_rate
if random.uniform (0.0, 1.0) < Ratio:
planned_event_type = 'particle'
planned_displacement = delta_s
target_particle = part
target_cell = vetoing_cell
break
delta_s += random_exponential (Q_tot)
# compile the list of particles that need separate treatment
extra_particles = surplus[:]
for k in excluded_cells:
part = cell_occupant[translated_cell (k, active_cell)]
if part is not None:
extra_particles.append (part)
# naive version of the short-range code by discretization
delta_s = 0.0
short_range_step = 1e-3
while delta_s < planned_displacement:
for possible_target_particle in extra_particles:
# this supposes a constant event rate over the time interval
# [delta_s:delta_s+short_range_step]
q = pair_event_rate (possible_target_particle[0] - active_particle[0] - delta_s,
possible_target_particle[1] - active_particle[1])
if q > 0.0:
event_time = random_exponential (q)
if event_time < short_range_step and delta_s + event_time < planned_displacement:
planned_event_type = 'particle'
planned_displacement = delta_s + event_time
target_particle = possible_target_particle
target_cell = cell_containing (target_particle)
break
delta_s += short_range_step
# advance active particle
distance_to_go -= planned_displacement
new_x = active_particle[0] + planned_displacement
active_particle = (new_x % 1.0, active_particle[1])
if planned_event_type == 'active-cell-change':
ac_x = (active_cell_limit + 0.5*cell_side) % 1.0
active_cell = cell_containing ([ac_x, active_particle[1]])
active_particle = (active_cell % L * cell_side, active_particle[1])
elif planned_event_type == 'particle':
# remove newly active particle from store
if target_particle in surplus:
surplus.remove (target_particle)
else:
cell_occupant[target_cell] = None
# put the previously active particle in the store
if cell_occupant[active_cell] is not None:
surplus.append (active_particle)
else:
cell_occupant[active_cell] = active_particle
active_particle = target_particle
active_cell = cell_containing (active_particle)
# restore particles vector for x <-> y transfer
particles = [ active_particle ]
particles += [ part for part in cell_occupant if part is not None ]
particles += surplus
# form histogram for computing radial distribution function g(r)
for k in range (len (particles)):
for l in range (k):
ibin = int (dist (particles[k], particles[l]) / histo_binwid)
if ibin < len (histo):
histo[ibin] += 1
hsamples += 1
# compute g(r) from histogram
half_bin = .5 * histo_binwid
r = np.arange (0., hbins) * histo_binwid + half_bin
g_of_r = histo / density / hsamples * 2
g_of_r /= math.pi * ((r+half_bin)**2 - (r-half_bin)**2)
# save g(r)
np.savetxt ('cvmc-radial-distr-func.dat', zip (r, g_of_r))