From Werner KRAUTH

Werner Krauth
Laboratoire de Physique Statistique
École normale supérieure
24 rue Lhomond
75231 Paris Cedex 05
France
Tel +33 (0) 44 32 25 50
werner.krauth@ens.f

CNRS Research Director (Theoretical Physics)

Director of the Physics Departement at Ecole normale supérieure, Paris, France (since January 2010)

Contents 1 Current research 1.1 Event-driven Monte Carlo algorithm for general potentials 1.2 Two-dimensional melting: First-order liquid-hexatic transition 2 Upcoming events 3 Text book 4 A picture book of algorithms

Current research

I am deeply interested in statistical physics and condensed matter physics, often in connection to computation and algorithms. Current interests are in hard spheres, mainly the melting transition in two-dimensional disks, bosons (in collaboration with the experimental groups at ENS), and the theory of convergence and of coupling in Markov chains. Practically all my work is in collaboration with colleagues and students.

Event-driven Monte Carlo algorithm for general potentials

In recent works, as for example on the melting transition in two dimensions, the event-chain algorithm has proven quite helpful. This hard-sphere Monte Carlo method runs a lot faster than earlier methods although the speed-uo remains constant for large system sizes. Nevertheless, gaining a factor of about 100 is not so bad for run-times (with the new algorithm) on the order of a few months... we got our results before it was time to retire.

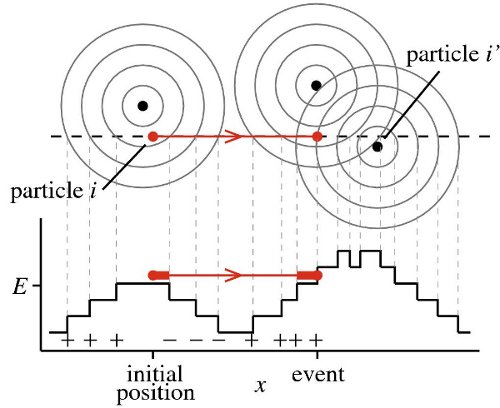
Recently, Etienne Bernard (now at MIT) and I were able to extend the event-chain algorithm to continuous potentials, and we are now quite excited: The algorithm allows to break detailed balance, it is (hopefully) much faster than local Monte Carlo algorithms, and it is extremely easy to program, to parallelize (hopefully), to modify and, why not, to improve. Technically, we work with stepped potentials (see the figure, similar approaches exist for molecular dynamics), but there is no problem going to finer and finer discretizations: the algorithm doesn't even slow down as we crank up the number of steps. But lots of things need to be done to understand this new approach, to check out possible applications, etc, and we are right now extremely busy.

Two-dimensional melting: First-order liquid-hexatic transition

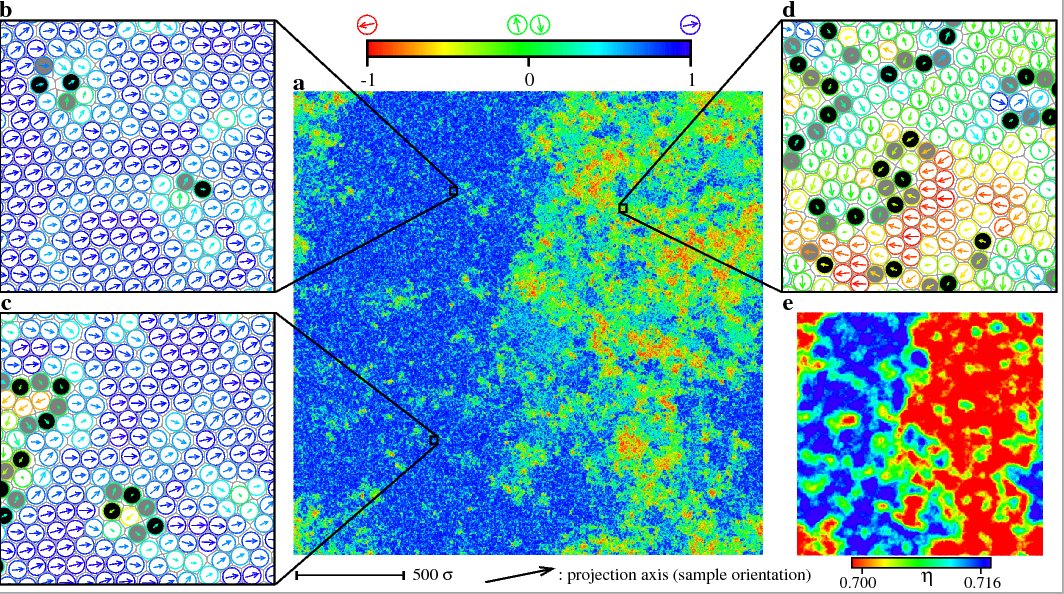
Here, I show the key figure of a recent paper, with Etienne Bernard, on the melting transition in hard disks. The main picture shows the orientations of a configuration with 1024x1024 disks, and two different regions are clearly visible: To the left, disks have more or less the same orientation, whereas to the right, the orientations vary (and the local densities are lower). To produce the picture, we used the

event-chain algorithm, a new Monte Carlo method that we developed a few years ago, with David Wilson. This algorithm is really the first one to outperform the classic Metropolis method from 1953. For a long time, I have been interested in the hard-disk melting problem, but an earlier attempt to speed up the extremely slow converge of numerical methods for this problem, the cluster algorithm that I developed with C. Dress, had failed.

Upcoming events

Summerschool: First Les Houches school in computational physics: soft matter June 20, 2011 - July 1, 2011, Les Houches, France

Workshop: PyPhy - Python in Physics 2011, August 29, 2011, ENS, Paris

Satellite meeting of the 4th European Meeting of Python in Science (Euroscipy 2011) also taking place at August 25-28, 2011, ENS, Paris

SimBioMa: Conference on Molecular Simulations in Biosystems and Material Science Sept. 28th - Oct. 1st 2011, Konstanz, Germany

University of Vienna, Austria (Seminar), Monday January 23rd, 2012

School of Physics and Astronomy, University of Nottingham, Great Britain, School Colloquium, Wednesday January 25th, 2012

University of Montpellier, France (Physics Colloquium), January 30th, 2012

Text book

A picture book of algorithms