From Werner KRAUTH

S. C. Kapfer, W. Krauth Cell-veto Monte Carlo algorithm for long-range systems arXiv:1606.06780 (2016)

Paper

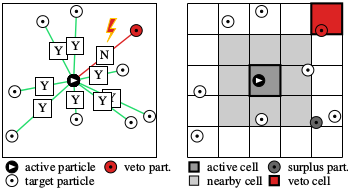
Abstract We present a rigorous efficient event-chain Monte Carlo algorithm for long-range interacting particle systems. Using a cell-veto scheme within the factorized Metropolis algorithm, we compute each single-particle move with a fixed number of operations. For slowly decaying potentials such as Coulomb interactions, screening line charges allow us to take into account periodic boundary conditions. We discuss the performance of the cell-veto Monte Carlo algorithm for general inverse-power-law potentials, and illustrate how it provides a new outlook on one of the prominent bottlenecks in large-scale atomistic Monte Carlo simulations.

Electronic version (from arXiv)

Illustration

The cell-veto algorithm is an application of the event-chain paradigm that was developed in 2009, with E. P. Bernard and D. B. Wilson, and much extended together with M. Michel and S. C. Kapfer, where we introduced the factorized Metropolis algorithm. In this algorithm, unlike in 99.9% of all simulation algorithms (Monte Carlo or Molecular dynamics), one does not compute the system energy in order to decide on a change of the physical system, but rather looks at all the interactions separately. So, if a particle a (the active particle), it has to ask all its partners t_1, t_2, .... (the target particles). If there is only a single veto, the move is not undertaken. What may sound weird is in fact