Main Page

From Werner KRAUTH

Revision as of 22:59, 9 December 2011; view current revision
←Older revision | Newer revision→
Jump to: navigation, search

Welcome to my new webpage (construction area)

Contents

Upcoming events

Summerschool: First Les Houches school in computational physics: soft matter June 20, 2011 - July 1, 2011, Les Houches, France

Workshop: PyPhy - Python in Physics 2011, August 29, 2011, ENS, Paris

Satellite meeting of the 4th European Meeting of Python in Science (Euroscipy 2011) also taking place at August 25-28, 2011, ENS, Paris

SimBioMa: Conference on Molecular Simulations in Biosystems and Material Science Sept. 28th - Oct. 1st 2011, Konstanz, Germany

Current research

I am deeply interested in statistical physics and condensed matter physics, often in connection to computation and algorithms. Current interests are in hard spheres, mainly the melting transition in two-dimensional disks, bosons (in collaboration with the experimental groups at ENS), and the theory of convergence and of coupling in Markov chains. Practically all my work is in collaboration with colleagues and students.

Event-driven Monte Carlo algorithm for general potentials

In recent works, as for example on the melting transition in two dimensions, the event-chain algorithm has proven quite helpful. This method, against initial beliefs, is in the same class as the local algorithm: it runs a lot faster than earlier methods, but the speed-uo remains constant for large system sizes. Nevertheless, gaining a factor of about 100 is not so bad, especially if the run-times (with the new algorithm), remain of the order of a few months.

Recently, we were able to extend the event-chain algorithm to continuous potential, which means that we are quite excited: The algorithm allows to break detailed balance, it is (hopefully) much faster than local Monte Carlo algorithms, and it is extremely easy to program, to parallelize (hopefully), to modify and, why not, to improve. Technically, we work with stepped potentials (similar approaches exist for molecular dynamics), but there is no problem going to finer and finer discretizations: the algorithm doesn't even slow down, as we crank up the number of discretization steps. But lots of things need to be done to understand the algorithm, possible applications, etc, and we are extremely busy right now.

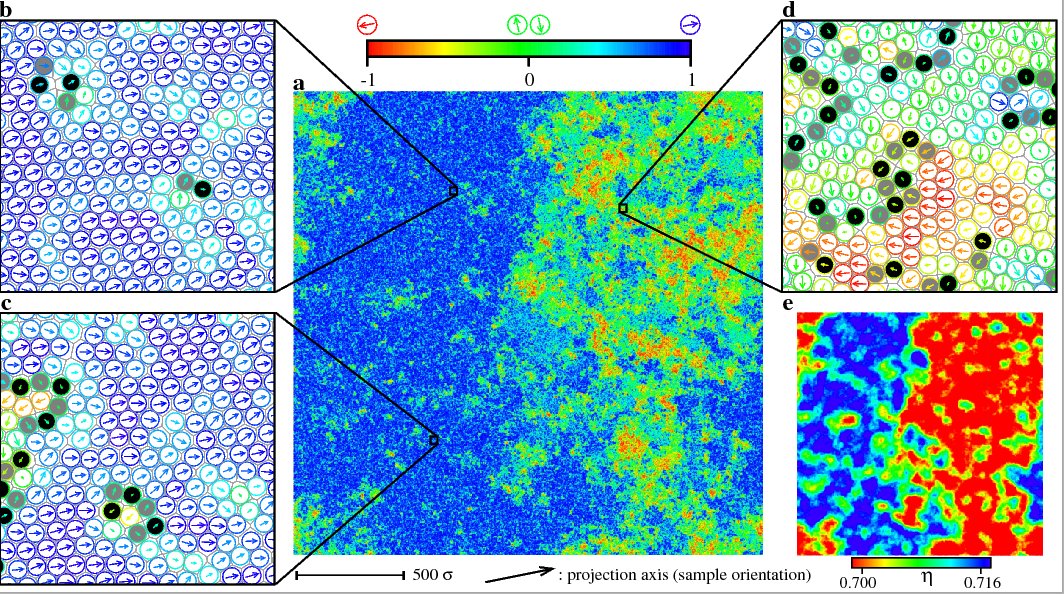
Two-dimensional melting: First-order liquid-hexatic transition

50px
Here, I show the key figure of a recent paper, with Etienne Bernard, on the melting transition in hard disks. The main picture shows the orientations of a configuration with 1024x1024 disks, and two different regions are clearly visible: To the left, disks have more or less the same orientation, whereas to the right, the orientations vary (and the local densities are lower). To produce the picture, we used the

event-chain algorithm, a new Monte Carlo method that we developed a few years ago, with David Wilson. This algorithm is really the first one to outperform the classic Metropolis method from 1953. For a long time, I have been interested in the hard-disk melting problem, but an earlier attempt to speed up the extremely slow converge of numerical methods for this problem, the cluster algorithm that I developed with C. Dress, had failed.

Text book

Cover of a book I wrote in 2006 Here is the book's website
Cover of a book I wrote in 2006 Here is the book's website


A picture book of algorithms

Direct-sampling algorithm for ideal bosons in a trap (see article with M. Holzmann). Adapted for interacting bosons, this algorithm was used in a variety of articles.
Direct-sampling algorithm for ideal bosons in a trap (see article with M. Holzmann). Adapted for interacting bosons, this algorithm was used in a variety of articles.
Event-chain Monte Carlo algorithm for hard spheres and related systems (see article with E. P. Bernard and D. B. Wilson, including Python implementation). This (fantastic) algorithm, about two orders of magnitude faster than local Monte Carlo, was used in our discovery of the first-order liquid-hexatic phase transition in hard disks.
Event-chain Monte Carlo algorithm for hard spheres and related systems (see article with E. P. Bernard and D. B. Wilson, including Python implementation). This (fantastic) algorithm, about two orders of magnitude faster than local Monte Carlo, was used in our discovery of the first-order liquid-hexatic phase transition in hard disks.


Exact diagonalization algorithm for Dynamical mean field theory (see article with M. Caffarel). This algorithm has been instrumental in our discovery of a first-order Mott transition in the Hubbard model in infinite dimensions. Much of our early work in the field is written up in our review with Georges, Kotliar, and Rozenberg
Exact diagonalization algorithm for Dynamical mean field theory (see article with M. Caffarel). This algorithm has been instrumental in our discovery of a first-order Mott transition in the Hubbard model in infinite dimensions. Much of our early work in the field is written up in our review with Georges, Kotliar, and Rozenberg
Rejection-free cluster algorithm for dimers (see article with R. Moessner). This algorithm was used for our discovery of a critical phase in three-dimensional dimer models (paper with Huse, Sondhi, and Moessner). Note that dimers flip about a symmetry axis between one valid configuration and another.
Rejection-free cluster algorithm for dimers (see article with R. Moessner). This algorithm was used for our discovery of a critical phase in three-dimensional dimer models (paper with Huse, Sondhi, and Moessner). Note that dimers flip about a symmetry axis between one valid configuration and another.
Alder and Wainwright's event-driven Molecular Dynamics algorithm (1957). (Animation by Maxim Berman).
Alder and Wainwright's event-driven Molecular Dynamics algorithm (1957). (Animation by Maxim Berman).


Research areas

Address

Werner Krauth
Laboratoire de Physique Statistique
École normale supérieure
24 rue Lhomond
75231 Paris Cedex 05
France
Tel +33 (0) 44 32 25 50
Image:Wernerkrauth.jpg
Retrieved from "http://www.lps.ens.fr/~krauth/index.php/Main_Page"
Personal tools