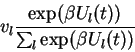Chapitre 4b
GÉRARD WEISBUCH
Laboratoire de Physique Statistique1
de l'Ecole Normale Supérieure,
24 rue Lhomond, F 75231 Paris Cedex 5, France.
email:weisbuch@physique.ens.fr
Les problèmes qui vont essentiellement nous intéresser dans ce
chapitre concernent les ``organisations'' au sens le
plus large, qui apparaissent sur un marché. En l'absence
d'organisation, on s'attend soit à ce que tous les comportements
imaginables soient observables chez les agents (hypothèse minimale),
soit à n'observer que des comportements optimaux. On
s'attend de même à ce que soit
les meilleurs produits l'emportent, soit, si leurs qualités
sont équivalentes, on imagine que n'importe quelle répartition
des parts de marché est a priori possible. Nous discuterons plus
loin d'autres exemples, mais face aux hypothèses les plus simples
comme l'uniformité des solutions et des comportements
ou on contraire la sélection de la solution optimale,
on observe souvent frappé dans la réalité des marchés
par la richesse des structures observables en terme
de répartition des parts de marchés, de comportement
des agents, des liens préférentiels pouvant s'établir
entre eux, du rôle des intermédiaires etc.
Au sens le plus large, ces structures s'interprètent
comme des institutions: croyances, routines, normes,
réseaux etc.
Le premier type de questions sur ces institutions
concerne leur fonction économique:
à quoi servent ces institutions? La réponse de
D. North (1990) relie ces institutions aux
incertitudes auxquelles doivent faire face les
agents économiques. Dans un situation dans laquelle
les conséquences d'un choix éventuel sont mal connues,
il peut être plus rationnel d'utiliser des routines de
comportement éprouvées que de rechercher à chaque étape
une solution optimale; on passe ainsi d'une rationalité
complète au niveau des actions à une rationalité procédurale
au niveau des comportements. Les institutions sont le résultat
de ces comportement stéréotypés.
Dans la même optique,
on peut essayer d'évaluer un bilan profits/pertes lié
à l'adoption de tel ou tel comportement: les institutions
adoptées optimiseraient ce bilan.
En fait, sans négliger l'intérêt de l'approche bilan,
on peut aussi se poser le problème de l'origine des institutions.
Dans cette optique, l'approche bilan ne donnerait qu'une perspective
finaliste à un problème de dynamique. Plus simplement, on
peut se demander si les institutions du marché sont le resultat d'une
sélection
(tout est pour le mieux dans le meilleur des mondes), ou
d'une histoire. Dans la même optique, une institution particulière
observée sur un marché donné est elle la mieux adaptée,
ou bien ne constitue-t-elle qu'une solution possible parmi un ensemble
(approche Arthur (1994)?
L'idée d'une dynamique à plusieurs attracteurs expliquant
ainsi l'apparition des structures différentes dans des situations
apparement équivalentes n'est pas toute réçente et elle a été
appliquée en économie par des auteurs tel que Arthur (sélection des
standards), Zeeman (1976) (comportement des marchés à partir de
la théorie des catastrophes), Guesnerie (le phénomène des
``tâches solaires'' et la prophétie auto-réalistrice).
L'urne de Polya, un système modèle des comportements d'imitation,
dans lequel à chaque tirage
l'utilisateur remet dans l'urne deux boules correspondant à
la couleur précédement tirée illustre bien la multiplicité des attracteurs
et l'importance des conditions initiales.
Figure:

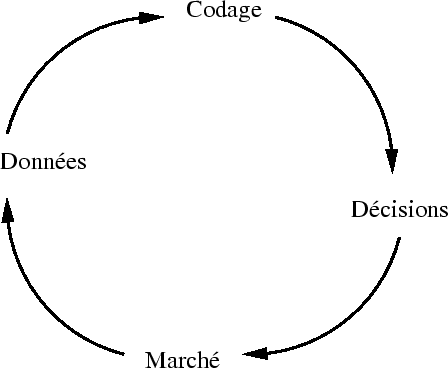 |
Principes canoniques
L'idée de base est que dans des conditions d'information imparfaite
les décisions des agents et leurs conséquences donnent lieu
à une dynamique d'apprentissage qui vient se coupler
à la dynamique des variables économiques.
Le schéma général de ces couplages apparaît sur la figure 1,
qui représente une boucle type de circulation
et traitement de l'information. L'information incomplète sur le marché
dont dispose un agent est codée par celui-ci (certains diraient même
qu'au départ l'agent ne dispose que de données brutes à partir desquelles
le codage crée l'information). C'est le codage, lié par son aspect
dynamique à l'apprentissage, qui permet à l'agent de filtrer et
d'organiser les données dont il dispose pour en retirer une "représentation
du monde" utilisable dans l'action. L'agent prend des décisions
en fonction de l'état du marché et de sa représentation du monde,
mais ces décisions influent elles-même sur l'état du marché. La boucle
se referme lorsque l'agent ré-actualise sa représentation du monde à
partir des nouvelles données qu'il reçoit à chaque instant.
L'état du marché est la résultante de l'ensemble des actions
des agents alors que les données acquises par chacun d'eux sont
le résultat d'un échantillonage forçément partiel
de celui-ci.
Dans les cas où la structure de l'information sur un
marché suit une dynamique dont la structure statique
est celle décrite ci-dessus, c'est à dire un
ensemble de boucles imbriquées, nous pouvons nous
attendre à observer les comportements dynamiques typiques des systèmes
complexes:
Attracteurs mutiples, chaos, structures "spatiales" au
sens le plus large, cad non seulement dans l'espace 2 ou 3d, mais dans
des espaces de produits, de prix, de conventions...
Dans un contexte économie et institutions,
la dynamique d'évolution vers l'un des attracteurs
possibles s'interprète comme un processus d'organisation:
la dynamique "sélectionne" les
configurations attractrices parmi la multitude initiale des possibles.
Le processus d'organisation peut aboutir à:
- l'apparitions de structures (par exemple en réseaux d'échange),
- l'émergence de nouvelle fonctions (intermédiaires)
- la sélection de produits, de routines, de conventions.
En pratique, un même problème est étudié en utilisant plusieurs
approches concomittantes:
- La résolution formelle d'un modèle simplifié à l'extrème.
Cette approche nous éclaire sur le fonctionnement du système
et sur les relations entre paramètres, variables et
comportements dynamiques résultants.
- La simulation numérique d'une batterie de modèles plus
réalistes non solubles par la méthode formelle,
qui nous permettent de vérifier la robustesse des conclusions
du modèle soluble.
Nous exposerons dans ce chapitre deux modèles simples
et une méthode formelle de résolution, celle du champ moyen,
sans décrire l'ensemble des simulations permettant de vérifier la
généricité des résultats établis par l'approche formelle.
Nous allons détailler ici les résultats généralisables
obtenus sur le problème de l'acheteur et du choix des
produits en appliquant un formalisme inspiré
de la mécanique statistique et en particulier du
``champ moyen''.
Nous considérons le problème d'un acheteur qui doit choisir
un produit (ou un vendeur) parmi d'autres. L'approche que nous allons
décrire est d'ailleurs applicable au problème plus général des acteurs
devant choisir une technologie,
une règle de comportement, une option politique etc.
Limitons nous dans cet exposé à deux exemples
extrêmes dans la gamme des informations disponibles pour l'acheteur.
- L'information est publique, mais les acheteurs ont la mémoire courte.
Ils basent leurs choix sur les choix des
autres agents à la période précédente (Föllmer 1974, Kirman 1993, Orlean
1995).
- L'information est privée et les agents se basent sur
l'histoire de leurs transactions précédentes (Weisbuch et al. 2000).
Suposons que les acheteurs ont une stratégie probabiliste
(que nous justifierons dans la suite de l'exposé).
Leur problème est alors de passer de l'ensemble 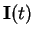 des informations dont ils disposent au temp
des informations dont ils disposent au temp 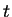 à une probabilité d'achat
à une probabilité d'achat 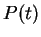 dans le simplex
dans le simplex 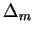 , où
, où 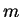 est le nombre des choix offerts.
est le nombre des choix offerts.
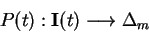 |
(1) |
Suivant l'approche décrite plus haut, nous décomposons
l'application 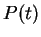 en deux:
en deux:
- une application de l'espace des informations
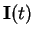 vers un espace de croyances
vers un espace de croyances  ; les
; les  représentent des indices subjectifs de performance attribués par
les acheteurs aux différents choix en fonction de l'information
partielle dont ils disposent.
représentent des indices subjectifs de performance attribués par
les acheteurs aux différents choix en fonction de l'information
partielle dont ils disposent.
- une seconde application de
 vers le simplex
vers le simplex 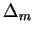 .
.
La première application est le codage de l'information, basé sur une
dynamique d'apprentissage, et la seconde le processus de choix
probabiliste.
Ce type de modèle existe sous de très nombreuses variantes.
Nous choisissons d'en exposer ici deux versions très simples
dans lesquels les acheteurs, en grand nombre 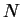 , doivent choisir
entre deux produits
, doivent choisir
entre deux produits 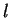 . Nous donnerons aussi des indications
sommaires sur d'autres variantes.
. Nous donnerons aussi des indications
sommaires sur d'autres variantes.
Dans le cas de l'information publique, on suppose en général que l'
établissement des indices  est basé sur un comportement d'imitation.
A chaque instant, un acheteur
est basé sur un comportement d'imitation.
A chaque instant, un acheteur 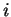 tiré au hasard est confronté
au choix d'un produit
tiré au hasard est confronté
au choix d'un produit 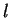 . Nous supposons qu'il connait le choix
des autres acteurs, ou plus précisement qu'il connait
le nombre
. Nous supposons qu'il connait le choix
des autres acteurs, ou plus précisement qu'il connait
le nombre 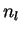 des acheteurs ayant acheté le produit
des acheteurs ayant acheté le produit 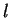 .
Bien entendu, les choix sont reversibles dans le sens où
un choix au temps
.
Bien entendu, les choix sont reversibles dans le sens où
un choix au temps 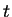 peut être remplacé par un autre
à un temps ultérieur.
A chaque pas de temps, l'indice de performance
peut être remplacé par un autre
à un temps ultérieur.
A chaque pas de temps, l'indice de performance 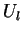 d'un acheteur
d'un acheteur 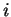 (les indices
(les indices 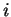 sont sous-entendus par la suite) pour le choix
sont sous-entendus par la suite) pour le choix 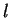 s'écrit:
s'écrit:
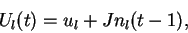 |
(2) |
où le premier terme correspond
à une préférence intrinsèque 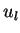 , indépendante
du choix des autres acheteurs, donc indépendant de
, indépendante
du choix des autres acheteurs, donc indépendant de 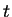 ,
et le second terme est le terme d'imitation
proportionnel au nombre
,
et le second terme est le terme d'imitation
proportionnel au nombre 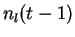 des acheteurs
ayant fait précedemment le choix
des acheteurs
ayant fait précedemment le choix 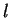 .
La constante d'interaction
.
La constante d'interaction
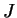 représente l'intensité du terme d'imitation par rapport
à la préférence intrinsèque
représente l'intensité du terme d'imitation par rapport
à la préférence intrinsèque 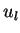 .
.
Dans le cas de l'information privée, nous supposons en
suivant Weisbuch etal. (2000) que les indices de performance
sont basés sur les expériences
antérieures de l'acheteur. Le modèle discuté ici s'applique
lorsque les qualités des produits
achetés fluctuent au cours du temps
pour des raisons tenant aussi bien aux qualités intrinsèques du
produit qu'à l'usage qui en est fait. On peut penser par exemple
à un produit alimentaire fruit ou légume, dont les variations
d'utilité peuvent être dues à son origine, aux traitements qu'il a
subi, au prix variable qu'en demande le vendeur, à sa
préparation par l'acheteur etc...
Le modèle s'applique en fait
au choix des vendeurs parmi ceux vendant un même type de produit,
par exemple sur un marché de denrées alimentaires périssables.
Sur ce type de marché où les vendeurs ne gardent pas de stock
sur le moyen terme, d'un jour à l'autre par exemple, la ``qualité''
d'un vendeur ne dépend pas seulement de ce qu'il peut vendre, mais
aussi de la disponibilité du produit.
A cause du couplage entre les choix des acheteurs et la disponibilité
des produits chez les différents vendeurs, le problème posé au
départ ne se ramène donc pas à un ensemble
d'acheteurs indépendants face à un ensemble de vendeurs.
L'information sur les qualités du produit
pour l'acheteur est donc codée
suivant un processus d'apprentissage
dans lequel l'acheteur "intègre" à chaque pas de temps
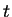 les "performances'' constatées
les "performances'' constatées 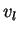 de ses choix antérieurs.
(Dans le cas du problème économique à l'origine de ce modèle,
le marché de gros du poisson à Marseille, les acheteurs
étaient en fait des détaillants, et les
de ses choix antérieurs.
(Dans le cas du problème économique à l'origine de ce modèle,
le marché de gros du poisson à Marseille, les acheteurs
étaient en fait des détaillants, et les 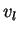 étaient
concrètement les profits réalisés par les acheteurs sur les
lots de poissons après leur distribution au détail).
étaient
concrètement les profits réalisés par les acheteurs sur les
lots de poissons après leur distribution au détail).
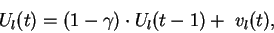 |
(3) |
Cette expression correspond au calcul d'une
moyenne flottante: le premier terme
décroit régulièrement l'influence des informations passées,
et le second prend en
compte le profit réalisé
si l'acheteur a fait le choix  au temps
au temps  (ce terme est nul si l'acheteur fait un choix autre que
(ce terme est nul si l'acheteur fait un choix autre que  ou bien si ayant choisi
ou bien si ayant choisi 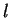 sa demande n'a pas été satisfaite).
Ce processus de moyenne flottante se justifie par la nécessité
pour l'acheteur de prendre
une moyenne pour amortir les fluctuations temporelles
tout en diminuant l'importance des informations trop
antérieures devenues non pertinentes.
sa demande n'a pas été satisfaite).
Ce processus de moyenne flottante se justifie par la nécessité
pour l'acheteur de prendre
une moyenne pour amortir les fluctuations temporelles
tout en diminuant l'importance des informations trop
antérieures devenues non pertinentes.
Nous supposons maintenant dans les deux cas de figure, information
publique et information privée, que les acheteurs choisissent chaque
possibilité 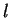 d'indice de perormance
d'indice de perormance
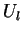 suivant une loi de probabilité:
suivant une loi de probabilité:
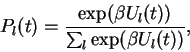 |
(4) |
où 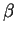 , le taux de discrimination
mesure la non-linéarité de la relation entre la
probabilité et l'indice
, le taux de discrimination
mesure la non-linéarité de la relation entre la
probabilité et l'indice 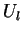 .
. 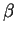 tendant vers l'infini correspond
au choix déterministe de l'indice le plus fort,
tendant vers l'infini correspond
au choix déterministe de l'indice le plus fort, 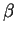 tendant
vers 0 à l'indifférence.
tendant
vers 0 à l'indifférence.
En effet,
un acheteur qui choisirait toujours le même produit après avoir
essayé initialement tous les produits offerts perdrait l'occasion
de bénéficier d'avantages apportés ultérieuriement aux autres produits:
De plus, une fois ``accroché'', il serait à la merci du vendeur
qui pourrait alors lui en offrir moins pour son argent. Sur un marché
changeant, un acheteur a intérêt à alterner sur le long terme entre les phases
où il achète le produit le meilleur suivant son évaluation et celles
où il teste le marché pour découvrir les meilleurs produits. C'est
le ``compromis exploration/exploitation'' proposé par ??
Les équations d'apprentissage pour l'information publique 2 et
de choix 4 s'appliquent à un large ensemble de modèles
. Pour pouvoir exposer ici une solution formelle
nous introduirons en plus certaines simplifications.
Nous prenons tout d'abord le cas le plus simple de deux vendeurs
``inertes'' dont les produits offrent une utilité intrinsèque constante
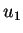 ou
ou 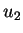 .
.
Ce cas simple est soluble dans l'approximation
du champ moyen consiste à remplacer
les variables 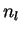 dans l'équation 2
par leur moyenne évaluée
à partir des probabilités exponentielles de l'équation 4.
Ce faisant nous négligeons les éventuelles
fluctuations par rapport à la valeur moyenne,
ce qui se justifie pour un grand nombre d'acheteurs
dans l'équation 2
par leur moyenne évaluée
à partir des probabilités exponentielles de l'équation 4.
Ce faisant nous négligeons les éventuelles
fluctuations par rapport à la valeur moyenne,
ce qui se justifie pour un grand nombre d'acheteurs 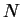 .
.
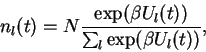 |
(5) |
Le système stochastique donné par les équations
2 et 4 devient alors un système déterministe
d'équations aux différences finies:
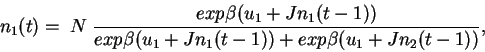 |
(6) |
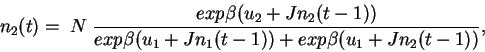 |
(7) |
et la différence entre les deux donne un équation aux différences
finies pour la variable
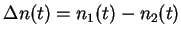 :
:
![\begin{displaymath}
\Delta n(t) \; = \; N \; Th [ \beta \; \frac{u_{1} - u_{2} +
J \Delta n(t-1)}{2}] ,
\end{displaymath}](img35.gif) |
(8) |
Les solutions invariantes 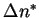 de cette équation
verifient:
de cette équation
verifient:
![\begin{displaymath}
\Delta n^* \; = \; N \; Th [ \beta \; \frac{u_{1} - u_{2} +
J \Delta n^*}{2}] ,
\end{displaymath}](img37.gif) |
(9) |
Figure:

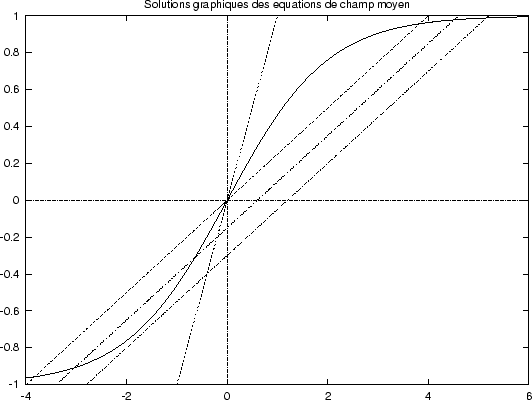 |
L'interprétation graphique de cette equation nous éclaire
immédiatement sur la nature des solutions: nous recherchons les
intersections d'une droite (le membre de gauche)
avec le graphe d'une fonction tangente
hyperbolique (le membre de droite),
c'est à dire d'une courbe en S. Suivant leurs pentes
respectives les deux courbes ont une ou trois intersections.
La transition entre les deux régimes se produit à  lorsque la pente de la droite est la même que celle
de la tangente hyperbolique à l'origine. Dans le cas symétrique:
lorsque la pente de la droite est la même que celle
de la tangente hyperbolique à l'origine. Dans le cas symétrique:
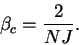 |
(10) |
Notons aussi que dans le cas des trois intersections,
seule les deux extrêmes sont
attractrices2.
Abordons maintenant l'interprétation de ces solutions
en termes de parts de marché.
Suivant les valeurs de 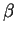 , le taux de discrimination,
on observe deux régimes dynamiques, séparés par une transition
abrupte.
, le taux de discrimination,
on observe deux régimes dynamiques, séparés par une transition
abrupte.
On peut aussi montrer que si au lieu d'un choix
binaire, l'acheteur est confronté à 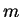 produits,
le coefficient critique
produits,
le coefficient critique 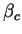 est multiplié par
est multiplié par 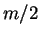 .
.
En développant la tangente hyperbolique au voisinage de l'origine
pour le cas symétrique où 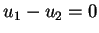 ,
on voit que la transition est abrupte:
,
on voit que la transition est abrupte: 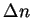 varie comme la puissance 1/2 de
la distance à la transition:
varie comme la puissance 1/2 de
la distance à la transition:
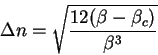 |
(12) |
Cette variation au voisinnage de la
transition est représenté sur la figure 3.
Figure:

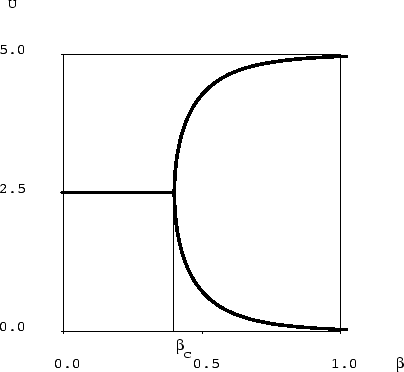 |
Figure:

 |
Au dessus de la transition, pour 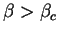 ,
l'existence des deux solutions stables asymétriques subsiste
aussi longtemps que la difference des utilités
intrinsèques reste inférieure à un certain seuil.
Si
,
l'existence des deux solutions stables asymétriques subsiste
aussi longtemps que la difference des utilités
intrinsèques reste inférieure à un certain seuil.
Si  la difference relative est définie par:
la difference relative est définie par:
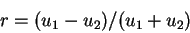 |
(13) |
les trois solutions subsistent pour:
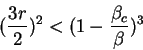 |
(14) |
Cette relation est obtenue en développant la
tangente hyperbolique au voisinage de 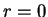 et du point critique
et du point critique  .
La figure 4 représente les solutions du vecteur de
.
La figure 4 représente les solutions du vecteur de
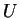 en fonction de la différence des
utilités intrinsèques dans le cas de
l'information publique.
en fonction de la différence des
utilités intrinsèques dans le cas de
l'information publique.
Etudions maintenant les évolutions possibles des indices
de performance. Supposons
que nous partions du cas pour lequel l'utilité intrinsèque
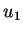 est largement supérieur
à
est largement supérieur
à 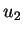 (la région à droite de la figure 4). Les acheteurs préfèrent
alors le produit 1 (
(la région à droite de la figure 4). Les acheteurs préfèrent
alors le produit 1 (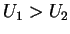 ).
Si les qualités du produit 2 évoluent
favorablement, par exemple grace aux efforts du producteur ou du vendeur),
on peut atteindre la région de co-existence des deux produits où les deux
attracteurs coexistent. Les acheteurs restent cependant fidèles
au produit 1, et ne passent au produit 2 que
lorsque la branche haute de la courbe de
).
Si les qualités du produit 2 évoluent
favorablement, par exemple grace aux efforts du producteur ou du vendeur),
on peut atteindre la région de co-existence des deux produits où les deux
attracteurs coexistent. Les acheteurs restent cependant fidèles
au produit 1, et ne passent au produit 2 que
lorsque la branche haute de la courbe de 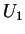 disparait, c'est à dire
au point où la tangente à la branche haute de
disparait, c'est à dire
au point où la tangente à la branche haute de 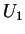 est verticale.
Si nous supposons maintenant une évolution en sens inverse,
c'est à dire la croissance relative de
est verticale.
Si nous supposons maintenant une évolution en sens inverse,
c'est à dire la croissance relative de 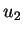 par rapport à
par rapport à 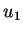 ,
c'est la branche inférieure du graphe de
,
c'est la branche inférieure du graphe de 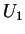 qui est alors décrite
jusqu'au point de tangence verticale
sur cette branche. Le point important
est que les points de tangence verticale sur chacune des courbes
qui est alors décrite
jusqu'au point de tangence verticale
sur cette branche. Le point important
est que les points de tangence verticale sur chacune des courbes
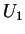 et
et 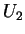 sont situés de part et d'autre de
l'égalité des utilités intrinsèques:
dans toute la région intermédiaire, le choix des acheteurs est dicté
par leurs choix antérieurs et non par la recherche du meilleur profit.
sont situés de part et d'autre de
l'égalité des utilités intrinsèques:
dans toute la région intermédiaire, le choix des acheteurs est dicté
par leurs choix antérieurs et non par la recherche du meilleur profit.
Le formalisme du champ moyen peut aussi s'appliquer
au cas de l'information privée et des équations 3.
Pour rendre le problème soluble analytiquement,
il est nécessaire d'ajouter des hypothèses supplémentaires:
- nous supposons que les vendeurs sont suffisament
approvisionés pour qu'un acheteur se présentant
chez l'un deux d'eux soit toujours servi.
- nous supposons de plus que dans ce cas,
les utilités intrinsèques observées sont
 ou
ou 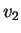 suivant le vendeur visité.
suivant le vendeur visité.
Les variations de 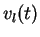 dans léquation 3
ne sont dues au fait qu'un acheteur peut visiter soit le vendeur 1
et alors
dans léquation 3
ne sont dues au fait qu'un acheteur peut visiter soit le vendeur 1
et alors
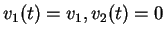 , soit le vendeur 2
et alors
, soit le vendeur 2
et alors
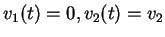 .
Ces hypothèses supplémentaires peuvent sembler contradictoires
avec l'algorithme de mise à jour de
.
Ces hypothèses supplémentaires peuvent sembler contradictoires
avec l'algorithme de mise à jour de 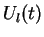 décrit par l'équation 3: celui-ci ne se justifie
que pour un environnement incertain. En fait ce qui nous interesse
vraiment n'est pas le modèle soluble, mais le modèle complet
en environnement incertain, c'est à dire avec fluctuation des
utilités intrinsèques dues en particulier à l'absence de stocks
illimités chez les vendeurs. L'intérêt de la résolution analytique
est de nous permettre de comprendre la dynamique d'une classe de
problèmes incluant le problème soluble, plus un ensemble
d'approximations qui ne peuvent être étudiées
que par simulation numérique. Cette classe de problèmes se définit par
leurs propriétés dynamiques communes, dites génériques.
décrit par l'équation 3: celui-ci ne se justifie
que pour un environnement incertain. En fait ce qui nous interesse
vraiment n'est pas le modèle soluble, mais le modèle complet
en environnement incertain, c'est à dire avec fluctuation des
utilités intrinsèques dues en particulier à l'absence de stocks
illimités chez les vendeurs. L'intérêt de la résolution analytique
est de nous permettre de comprendre la dynamique d'une classe de
problèmes incluant le problème soluble, plus un ensemble
d'approximations qui ne peuvent être étudiées
que par simulation numérique. Cette classe de problèmes se définit par
leurs propriétés dynamiques communes, dites génériques.
Dans le cas de deux vendeurs
ou de deux marques offrant des produits d'utilité
intrinsèque constante
 et
et 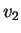 , la recherche des attracteurs de la dynamique
fait alors intervenir des équations équivalentes aux équations
5-13 à quelques changements près
de paramètres (
, la recherche des attracteurs de la dynamique
fait alors intervenir des équations équivalentes aux équations
5-13 à quelques changements près
de paramètres (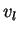 au lieu de
au lieu de 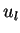 ) et de variables
(les utilités
) et de variables
(les utilités 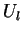 au lieu du nombre
au lieu du nombre 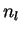 des acheteurs
ayant choisi l'un des produits).
L'approximation du champ moyen consiste à remplacer dans l'équation
3
des acheteurs
ayant choisi l'un des produits).
L'approximation du champ moyen consiste à remplacer dans l'équation
3 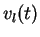 par son espérance mathématique :
par son espérance mathématique :
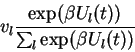 |
(15) |
Cette approximation est plus difficile à justifier
que dans le cas de l'information publique, mais on peut vérifier
sa validité par les simulations numériques: on voit ainsi qu'elle
s'applique si le coefficient d'atténuation 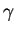 intervenant dans
l'équation 3 est petit, ce qui correspond bien à prendre
en compte dans l'évaluation de
intervenant dans
l'équation 3 est petit, ce qui correspond bien à prendre
en compte dans l'évaluation de 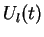 nombre ``effectif'' d'échantillons de l'ordre de
nombre ``effectif'' d'échantillons de l'ordre de  .
L'équation des points fixes en
.
L'équation des points fixes en
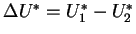 devient:
devient:
![\begin{displaymath}
\gamma \Delta U^* - \frac{v_1-v_2}{2}
= \frac{v_1+v_2}{2} \; Th [\frac{\beta \Delta U^*}{2}].
\end{displaymath}](img80.gif) |
(16) |
Cette équation en 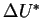 qui ressemble fort
à l'équation 9 en
qui ressemble fort
à l'équation 9 en 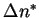 obtenue dans le
cas de l'information publique.
Le méthode de résolution est donc analogue.
On observe ainsi deux régimes séparés par une transition de
phase abrupte à
obtenue dans le
cas de l'information publique.
Le méthode de résolution est donc analogue.
On observe ainsi deux régimes séparés par une transition de
phase abrupte à 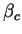 tel que:
tel que:
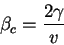 |
(17) |
où
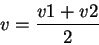 |
(18) |
- Si
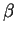 est faible, ce qui correspond à un régime désordonné,
l'acheteur visite indifférement l'un ou l'autre vendeur.
est faible, ce qui correspond à un régime désordonné,
l'acheteur visite indifférement l'un ou l'autre vendeur.
- Au contraire, pour les fortes valeurs de
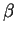 les croyances
les croyances
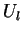 sont très
contrastées, et l'acheteur visite systématiquement
l'un des vendeurs: la fidélité à l'un des vendeurs prédomine,
même dans le cas symétrique (
sont très
contrastées, et l'acheteur visite systématiquement
l'un des vendeurs: la fidélité à l'un des vendeurs prédomine,
même dans le cas symétrique ( ).
Celui des vendeurs qui l'emporte est essentiellement
déterminé par les conditions initiales et non par les utilités intrinsèques.
).
Celui des vendeurs qui l'emporte est essentiellement
déterminé par les conditions initiales et non par les utilités intrinsèques.
Toutes les propriétés démontrées dans le cas de
l'information publique s'appliquent, caractère abrupte de la transition
(équation 12) et bien sûr hysteresis
du choix des acheteurs lors des variations
des utilités intrinsèques des
produits achetés chez les différents vendeurs.
Pour un nombre 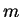 des vendeurs, le paramètre critique devient:
des vendeurs, le paramètre critique devient:
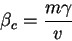 |
(19) |
Toutes ces propriétés dynamiques prédites pour le modèle
simple ci-dessus sont vérifiées par simulation numérique
pour une gamme de modèles équivalents pour
lesquels par exemple les vendeurs n'offrent
à la vente que des quantités finies
et observent des stratégies plus réalistes d'approvisionnement et
de fixation du prix de vente.
Le type d'organisation observée diffère cependant
entre le cas de l'information publique et celui de
l'information privéee.
Dans le cas de l'information publique, l'un des produits
l'emporte sur l'autre en termes de part de marché.
C'est le schéma décrit par Arthur, Orlean, Durlauf...
Le processus d'imitation entraine l'uniformité des choix
et le marché tout entier est organisé ainsi.
Au contraire, dans le cas de l'information privée,
les croyances des acheteurs peuvent différer en fonction
de leurs expériences;
le processus de mémorisation concerne chacun d'entre eux
individuellement:
certains acheteurs préfèrent systématiquement
un produit, d'autres acheteurs l'autre.
Le processus d'organisation concerne le comportement des
individus et ne conduit pas à l'élimination d'un produit par l'autre.
L'hétérogénéité des caractéristiques des acheteurs conduit
elle aussi à des différences suivant le caractère de l'information.
En effet, les acheteurs d'un marché
présentent des caractéristiques différentes,
et on peut supposer dans le cas général une distribution
telle que certains acheteurs aient des de caractéristiques
les plaçant dans le régime organisé alors que d'autres seraient
dans le régime désordonné.
- Dans le cas de l'imitation, on observe soit un régime organisé pour
l'ensemble des acheteurs avec un produit dominant presque totalement le
marché, ou bien, au contraire le régime désordonné.
- Au contraire, dans le cas de la
mémorisation, certains acheteurs sont fidèles à l'un des produits et les
autres ont un comportement désordonné et achètent apparement au hasard un
produit ou l'autre. Ordre et désordre co-existent. Cependant, la
distribution des comportements est bi-modale, ce qui traduit le caractère
abrupt de la transition3.
Dans le cas de l'information publique,
l'approximation du champs moyen s'applique bien lorsque
chaque tous les acheteurs connaissent les choix de tous les autres
acheteurs, ou au moins les parts de marchés. On peut essayer
de s'affranchir de cette hypothèse d'information globale en
considérant des modèles de type réseau social,
dans lesquels les acheteurs ne connaissent qu'un petit nombre
d'autres acheteurs et basent leur choix sur ceux des acheteurs avec lesquels
ils sont connectés. Ces modèles sont souvent représentés par des
réseaux carrés, mais le concept s'applique d'une manière
plus générale aux réseaux aléatoires. Dans le cas des réseaux
dilués (c'est à dire lorsque le nombre de connexions
par acheteur est petit par rapport au nombre des acheteurs),
la phase ordonnée peut n'être pas homogène: le réseau des acheteurs se
structure en domaines réguliers de choix uniforme séparés par des
parois. Il peut donc y avoir une homogénéité locale, et hétérogénéité
globale.
Le même type de formalisme s'applique du point de vue des vendeurs
qui souhaitent conquérir un marché. Partant de conditions initiales
avec mélange des choix,
la dynamique fait apparait dans le réseau des acheteurs, des
patterns spatio-temporels dont la nature est liée aux différences
des préférences intrinsèque.
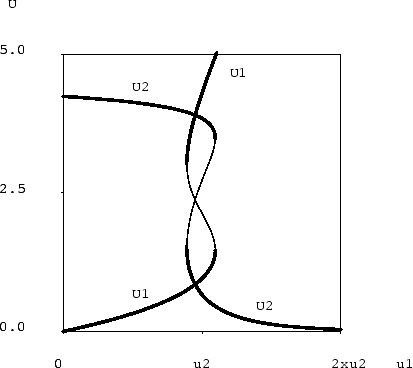
La figure 5 montre les domaines stables (ou plus précisément méta-stables),
atteints à partir d'une distribution initiale aléatoire hors
d'équilibre dans la mesure où la majeure partie des acheteurs
a choisi le produit de plus petite préférence intrinsèque.
On remarquera la forme régulière en rectangle des domaines
de choix uniforme.
Figure:

 |
La discussion ci-dessus illustre bien
le type de structure résultant des interactions entre les processus
d'apprentissage des agents et les processus économiques:
- Multiplicités des attracteurs, même dans le cas ou la disymétrie
des produits devrait favoriser l'un d'eux;
- importance des conditions ou des fluctuations initiales;
- apparition de structures spatiales et de réseaux préférentiels.
L'interprétation des structures observées en terme d'attracteurs
conduit à d'importantes conséquences:
- L'attractivité dans l'espace des variables se traduit
par une propriété de résilience dans l'espace des
paramètres: si l'on varie un paramètre du système
le système ne change que très peu tant qu'il reste
sur le même attracteur; mais si cet attracteur devient instable,
le système change brusquement d'attracteur. Cette réponse en
tout ou rien suivant l'intensité du changement de paramètre est très
différente d'une réponse linéaire.
- On peut aussi en déduire une propriété de
généricité du modèle: les modèles décrits sont évidement
ultra-simplifiés et l'on peut se poser la question de
savoir comment les résultats dépendent de ces simplifications.
En fait les simulations numériques permettent de tester toute
une classe de modèles de complexité croissante couplant par exemple
la dynamique des vendeurs à celles des acheteurs sur un marché.
Les simulations montrent ainsi des comportements similaires
dans un ensemble de modèles, au moins au niveau des attracteurs.
Cette notion de classe d'universalité des modèles est liée
à une dynamique avec attracteurs et se rapproche de la notion
de stabilité structurelle en théorie des catastrophes.
- En poursuivant plus loin cette notion de propriétés génériques
liées aux attracteurs, on peut conjecturer que s'il on était capable
de construire un modèle ``fidèle'' du marché réel, ce modèle
appartiendrait à la même classe d'universalité que les modèles
testé numériquement et vérifierait donc les même propriétés génériques.
Autrement dit, on aboutit à une notion différente de ``vérification''
d'un modèle théorique par une réalité empirique.
Il ne s'agit plus de tester toutes les prédictions du modèle,
mais seulement les propriétés génériques liées aux attracteurs,
en sachant bien que d'autres propriétés,
comme par exemple le niveau atteint par certaines variables
ou la nature précise de certains processus, ne sont
pas déterminantes.
- Notons enfin qu'en se restreignant à une
description en termes d'attracteurs, on discrétise l'espace des
paramètres en régions correspondant à un type d'attracteur
(régimes dynamiques). C'est cette discrétisation qui nous
permet de reconnaître des faits stylisés et de caractériser des
régimes empiriques, alors qu'a priori on pourrait s'attendre
à observer un continuum amorphe des comportements.
Nous n'avons explicité dans ce chapitre qu'une seule méthode
que nous n'avons appliquée qu'à deux cas de figures très stylisés
concernant le comportement des acheteurs. La problématique
est aussi applicable aux comportements des vendeurs et
à l'émergence possible des diverses fonctions d'intermédiaires
(grossistes, banques, commissaires priseurs, market makers...).
Une importante littérature s'est développée à propos
du comportement des agents boursiers à partir d'abord de
simulations multi-agents (Arthur et al. 1997)
puis autour d'un modèle stylisé dans lequel les agents
chercher à réaliser l'inverse d'un comportement moutonnier,
dans l'idée qu'il vaut mieux précéder que suivre.
Cette littérature est connue sous les noms d'El Farrol
bar problem et jeu de la minorité (Challet and Y.-C. Zhang 1998).
Le problème stylisé est soluble par une méthode formelle
dite des répliques: bien que les séries temporelles
apparaissent chaotiques, des structures organisées peuvent apparaître
dans l'espace des stratégies des acteurs.
Un autre exemple d'organisation, sur le marché du fermage,
est donné par la distribution discrète des termes de contrat
de fermage (P. Young). Bien entendu, on aimerait pouvoir
aussi aborder le rôle des institutions plus complexes
comme les bourses, voir même la possibilité que des
structures politico-sociales soient engendrées
(avec boucles de rétro-action) par le marché:
on peut penser en particulier à la tribu en relation
avec les marchés des produits agricoles (Kohler 1993)
et à l'apparition des banques et du pouvoir des
Medicis à Florence à la fin du moyen âge
en relation avec le commerce international (Padgett 1993).
Anderson S. P., A. de Palma and J.F. Thisse (1993),
Discrete Choice Theory of Product Differentiation,
Cambridge (MA): MIT Press.
Aoki M. (1996), A New Approach to Macroeconomic Modelling, New
York: Cambridge University Press.
Arthur, B. W. (1994)
``Increasing Returns and Path Dependence in the Economy'',
(University of Michigan Press).
Arthur, B.W. and D.A. Lane (1993), "Information Contagion",
Structural Changes and Economic Dynamics, 4, 81-104.
Arthur W.B., J.H. Holland, B. LeBaron, R.G. Palmer, and P. Tayler (1997),
"Asset Pricing under Endogenous Expectations in an Artificial
Stock Market", in: W.B. Arthur, D. Lane and S.N. Durlauf (eds),
The Economy as an Evolving, Complex System II, 15-44.
Blume L. (1993), "The Statistical Mechanics of Strategic Interaction",
Games and Economic Behaviour, 5, 387-424.
Brock W.A. and S.N. Durlauf (1995), "Discrete Choices with Social
Interactions I: Theory", Working Paper 95-10-084,
Santa Fe Institute, Santa Fe, NM.
Brout, E. (1965), Phase Transitions, New York (NY): Benjamin.
D. Challet and Y.-C. Zhang, ``On the Minority Game : Analytical and
Numerical Studies'', Physica A 256, 514 (1998)
Derrida B. (1986) "Phase Transitions in Random Networks of Automata"
in: J. Souletie, J. Vannimenus and R. Stora (eds), Chance and Matter,
New York (NY): North-Holland.
Durlauf S. (1990), "Locally Interacting Systems, Coordination Failure and
the Behaviour of Aggregate Activity", mimeo, Stanford University,
Stanford, CA.
Diamond P. (1989), "Search Theory", in: J. Eatwell, M. Milgate and P. Newman
(eds), The New Palgrave: A Dictionary of Economics, London (UK):
Macmillan, 273-79.
Föllmer H. (1974) "Random Economies with Many Interacting Agents",
Journal of Mathematical Economics, 1/1, 51-62.
Herreiner, D. (1997), "Market Organization", mimeo, University
of Bonn.
Jackson M. and A.Wolinsky (1996), "A Strategic Model of Social and Economic
Networks", Journal of Economic Theory, 71, 44-74.
Kilani, K. and J. Lesourne (1995), "Endogeneous Preferences,
Self-Organizing Systems and Consumer Theory", Mimeo 95-6,
Laboratoire d'Econométrie, Conservatoire National des Arts et
Métiers, Paris.
Kirman, A.P. and A. Vignes (1991), "Price Dispersion. Theoretical
Considerations and Empirical Evidence from the Marseilles Fish Market",
in K.G. Arrow (ed), Issues in Contemporary Economics, London
(UK): Macmillan.
Kirman A.P. (1993), "Ants, Rationality and Recruitment",
Quarterly Journal of Economics, 108, 137-156
Kirman, A.P. and N. Vriend (1995), "Evolving Market Structure: A Model of
Price Dispersion and Loyalty", mimeo, Department of Economics,
Virginia Polytechnic Institute and State University, Blacksburg, VA.
Kohler T.A. (1993)
``The Calculus of Self Interest in the Development of Cooperation:
Sociopolitical Development and Risk among the Northern Anasazi''
Santa Fe Insttitute Working Paper 93-06-033.
Lesourne, J. (1992), The Economics of Order and Disorder,
Oxford: Clarendon Press.
Luce, D.R. (1959), Individual Choice Behaviour, New York (NY):
Wesley.
Marimon R. (1996), "Learning in Economics", Working Paper 96/12,
Department of Economics, European University Institute, Florence, Italy.
Orléan A. (1995), "Bayesian Interactions and Collective Dynamics of
Opinions: Herd Behavior and Mimetic Contagion", Journal of
Economic Behavior and Organization, 28, 257-274.
Padgett J. (1993) "Robust Action and the Rise of the Medici, 1400-1434"
American Journal of Sociology .
Pfeuty, P., Toulouse, G. (1977), Introduction to the
Renomalization Group and to Critical Phenomena, New York (NY): Wiley.
Vriend N. (1994), "Self-Organized Markets in a Decentralized Economy",
Working Paper 94-03-013, Santa Fe Institute, Santa Fe, NM.
Weisbuch G. (1990), Complex Systems Dynamics, Redwood City
(CA): Addison Wesley.
Weisbuch G., Kirman A. and Herreiner D. (2000),
``Market Organisation and Trading Relationships''
Economic Journal.
Zeeman C. (1976),``Catastrophy Theory'' Scientific American, 234, 4,
65-83.
Chapitre 4b
This document was generated using the
LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split +0 chapa.tex
The translation was initiated by weisbuch on 2000-09-07
Footnotes
- ... Statistique1
-
Laboratoire associé au CNRS (URA 1306), à l'ENS et
aux Universités Paris 6 et Paris 7
- ... attractrices2
- un diagramme analogue à la figure
2 permet d'itérer l'équation aux différences finies 8
et de vérifier l'attractivité des intersections extrêmes
et le caractère répulsif de la solution intermédiaire.
- ... transition3
- la bi-modalité de la distribution
des comportements constitute un signature de la transition de phase
testable sur un ensemble de données empiriques (Weisbuch etal. 2000)
weisbuch
2000-09-07

![]() des informations dont ils disposent au temp
des informations dont ils disposent au temp ![]() à une probabilité d'achat
à une probabilité d'achat ![]() dans le simplex
dans le simplex ![]() , où
, où ![]() est le nombre des choix offerts.
est le nombre des choix offerts.
![]() en deux:
en deux:
![]() , doivent choisir
entre deux produits
, doivent choisir
entre deux produits ![]() . Nous donnerons aussi des indications
sommaires sur d'autres variantes.
. Nous donnerons aussi des indications
sommaires sur d'autres variantes.
![]() est basé sur un comportement d'imitation.
A chaque instant, un acheteur
est basé sur un comportement d'imitation.
A chaque instant, un acheteur ![]() tiré au hasard est confronté
au choix d'un produit
tiré au hasard est confronté
au choix d'un produit ![]() . Nous supposons qu'il connait le choix
des autres acteurs, ou plus précisement qu'il connait
le nombre
. Nous supposons qu'il connait le choix
des autres acteurs, ou plus précisement qu'il connait
le nombre ![]() des acheteurs ayant acheté le produit
des acheteurs ayant acheté le produit ![]() .
Bien entendu, les choix sont reversibles dans le sens où
un choix au temps
.
Bien entendu, les choix sont reversibles dans le sens où
un choix au temps ![]() peut être remplacé par un autre
à un temps ultérieur.
A chaque pas de temps, l'indice de performance
peut être remplacé par un autre
à un temps ultérieur.
A chaque pas de temps, l'indice de performance ![]() d'un acheteur
d'un acheteur ![]() (les indices
(les indices ![]() sont sous-entendus par la suite) pour le choix
sont sous-entendus par la suite) pour le choix ![]() s'écrit:
s'écrit:
![]() les "performances'' constatées
les "performances'' constatées ![]() de ses choix antérieurs.
(Dans le cas du problème économique à l'origine de ce modèle,
le marché de gros du poisson à Marseille, les acheteurs
étaient en fait des détaillants, et les
de ses choix antérieurs.
(Dans le cas du problème économique à l'origine de ce modèle,
le marché de gros du poisson à Marseille, les acheteurs
étaient en fait des détaillants, et les ![]() étaient
concrètement les profits réalisés par les acheteurs sur les
lots de poissons après leur distribution au détail).
étaient
concrètement les profits réalisés par les acheteurs sur les
lots de poissons après leur distribution au détail).
![]() d'indice de perormance
d'indice de perormance
![]() suivant une loi de probabilité:
suivant une loi de probabilité:
![]() dans l'équation 2
par leur moyenne évaluée
à partir des probabilités exponentielles de l'équation 4.
Ce faisant nous négligeons les éventuelles
fluctuations par rapport à la valeur moyenne,
ce qui se justifie pour un grand nombre d'acheteurs
dans l'équation 2
par leur moyenne évaluée
à partir des probabilités exponentielles de l'équation 4.
Ce faisant nous négligeons les éventuelles
fluctuations par rapport à la valeur moyenne,
ce qui se justifie pour un grand nombre d'acheteurs ![]() .
.
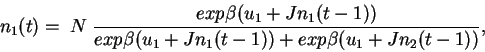
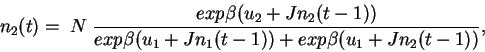
![]() :
:
![]() lorsque la pente de la droite est la même que celle
de la tangente hyperbolique à l'origine. Dans le cas symétrique:
lorsque la pente de la droite est la même que celle
de la tangente hyperbolique à l'origine. Dans le cas symétrique:
![]() , le taux de discrimination,
on observe deux régimes dynamiques, séparés par une transition
abrupte.
, le taux de discrimination,
on observe deux régimes dynamiques, séparés par une transition
abrupte.
![]() produits,
le coefficient critique
produits,
le coefficient critique ![]() est multiplié par
est multiplié par ![]() .
.
![]() ,
on voit que la transition est abrupte:
,
on voit que la transition est abrupte: ![]() varie comme la puissance 1/2 de
la distance à la transition:
varie comme la puissance 1/2 de
la distance à la transition:
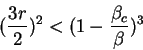
![]() est largement supérieur
à
est largement supérieur
à ![]() (la région à droite de la figure 4). Les acheteurs préfèrent
alors le produit 1 (
(la région à droite de la figure 4). Les acheteurs préfèrent
alors le produit 1 (![]() ).
Si les qualités du produit 2 évoluent
favorablement, par exemple grace aux efforts du producteur ou du vendeur),
on peut atteindre la région de co-existence des deux produits où les deux
attracteurs coexistent. Les acheteurs restent cependant fidèles
au produit 1, et ne passent au produit 2 que
lorsque la branche haute de la courbe de
).
Si les qualités du produit 2 évoluent
favorablement, par exemple grace aux efforts du producteur ou du vendeur),
on peut atteindre la région de co-existence des deux produits où les deux
attracteurs coexistent. Les acheteurs restent cependant fidèles
au produit 1, et ne passent au produit 2 que
lorsque la branche haute de la courbe de ![]() disparait, c'est à dire
au point où la tangente à la branche haute de
disparait, c'est à dire
au point où la tangente à la branche haute de ![]() est verticale.
Si nous supposons maintenant une évolution en sens inverse,
c'est à dire la croissance relative de
est verticale.
Si nous supposons maintenant une évolution en sens inverse,
c'est à dire la croissance relative de ![]() par rapport à
par rapport à ![]() ,
c'est la branche inférieure du graphe de
,
c'est la branche inférieure du graphe de ![]() qui est alors décrite
jusqu'au point de tangence verticale
sur cette branche. Le point important
est que les points de tangence verticale sur chacune des courbes
qui est alors décrite
jusqu'au point de tangence verticale
sur cette branche. Le point important
est que les points de tangence verticale sur chacune des courbes
![]() et
et ![]() sont situés de part et d'autre de
l'égalité des utilités intrinsèques:
dans toute la région intermédiaire, le choix des acheteurs est dicté
par leurs choix antérieurs et non par la recherche du meilleur profit.
sont situés de part et d'autre de
l'égalité des utilités intrinsèques:
dans toute la région intermédiaire, le choix des acheteurs est dicté
par leurs choix antérieurs et non par la recherche du meilleur profit.
![]() et
et ![]() , la recherche des attracteurs de la dynamique
fait alors intervenir des équations équivalentes aux équations
5-13 à quelques changements près
de paramètres (
, la recherche des attracteurs de la dynamique
fait alors intervenir des équations équivalentes aux équations
5-13 à quelques changements près
de paramètres (![]() au lieu de
au lieu de ![]() ) et de variables
(les utilités
) et de variables
(les utilités ![]() au lieu du nombre
au lieu du nombre ![]() des acheteurs
ayant choisi l'un des produits).
L'approximation du champ moyen consiste à remplacer dans l'équation
3
des acheteurs
ayant choisi l'un des produits).
L'approximation du champ moyen consiste à remplacer dans l'équation
3 ![]() par son espérance mathématique :
par son espérance mathématique :