A most general characteristic equation can be deduced from:
where x and y are the deviations from
equilibrium values and A,B,C,D the 0 of the linear
expansion of the dynamical system.
The characteristic equation in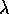 
is then:
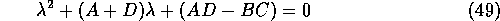
and the discriminant:
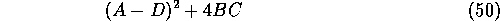
Oscillations occur when the discriminant is negative. A necessary condition is that BC<0. An interpretation of the fact that couplings should be much larger than diagonal terms in the linearized equations is that the system should be "truly" 2-dimensional. Otherwise the "fast" variable simply follows the "slow" variable decay towards equilibrium.