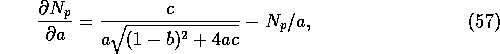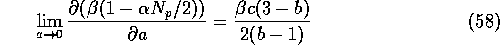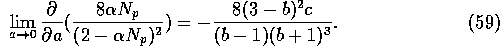Next: References
Up: Appendix
Previous: Conditions for oscillations
Here we present the analysis for the case described in Section 4, of
prices with a lower bound.
Suppose that
prices time 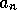 are given by equation 39 with
are given by equation 39 with 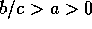 , so that prices
decrease from a maximum of
, so that prices
decrease from a maximum of 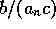 toward a minimum of
toward a minimum of 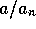 . In order to
make comparisons with the results of the other sections, a reasonable assumption is that the minimum price is
lower than under the constant price regime of section 2, i.e. that
. In order to
make comparisons with the results of the other sections, a reasonable assumption is that the minimum price is
lower than under the constant price regime of section 2, i.e. that
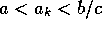 , where
, where 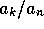 is the price of section 2. Using equation 39
implies that there is no limit on the income from selling
the harvest, as there is when a=0. However,as long as a is small
compared to 1, we expect that the results given for the a=0 case
will essentially hold: namely that a nonzero equilibrium only exists
when b is above a minimum value near
is the price of section 2. Using equation 39
implies that there is no limit on the income from selling
the harvest, as there is when a=0. However,as long as a is small
compared to 1, we expect that the results given for the a=0 case
will essentially hold: namely that a nonzero equilibrium only exists
when b is above a minimum value near 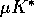 ,
and that (when
,
and that (when 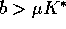 ) the
equilibrium resource level is larger,
the equilibrium is more strongly attracting,
and oscillations are less likely than in the constant price case. However,
as a moves away from zero and price supports become stronger, we would
like to know how this affects the a=0 results.
) the
equilibrium resource level is larger,
the equilibrium is more strongly attracting,
and oscillations are less likely than in the constant price case. However,
as a moves away from zero and price supports become stronger, we would
like to know how this affects the a=0 results.
When a > 0 the nonzero equilibrium of the nondimensionalized system
with 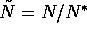 ,
, 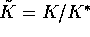 (
(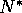 ,
, 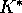 given by equation 5)
is
given by equation 5)
is 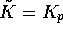 ,
, 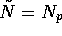 , where
, where
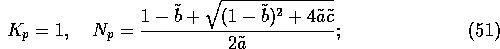
and we define 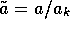 ,
,
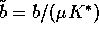
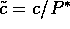 , and
, and
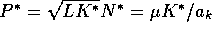 .
.
As we found in section 4, adding prices does not change the equilibrium
capital but significantly affects the equilibrium resource.
However, unlike the a=0 case, N-p is positive for all positive
values of b. What is different now is that if b<1 then
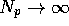 as
as 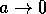 while if b>1 then
while if b>1 then 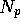 approaches the a=0
value as
approaches the a=0
value as 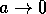 .
.
Letting
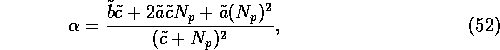
and linearizing about the nontrivial equilibrium,
we find that the eigenvalues of this system are:
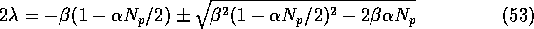
These eigenvalues always have negative real part. This can be seen
via the following argument. Note that in the remaining discussion of this section,
we drop the tildes.
Since 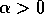 , these eigenvalues both have negative real part when
, these eigenvalues both have negative real part when
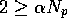 . Using the relationship between a, b, c and
. Using the relationship between a, b, c and 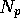 to
replace each
to
replace each 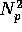 , this
condition on
, this
condition on 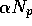 can be rewritten as
can be rewritten as
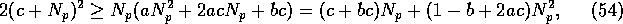
or
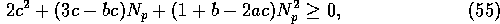
and applying the equality again shows that this is always true. Thus this
is always a stable equilibrium point. It is a stable spiral point when
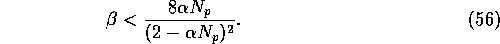
In the limit as 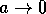 , these results approach those found in section 3.
We expect that increasing a will have the effect of 0 the impact of
decreasing prices, and, in fact, increasing
the lower bound on prices,
, these results approach those found in section 3.
We expect that increasing a will have the effect of 0 the impact of
decreasing prices, and, in fact, increasing
the lower bound on prices, 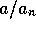 ,
decreases the equilibrium level of the resource,
,
decreases the equilibrium level of the resource, 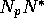 .
However, the dependence of the eigenvalues
on a is much more subtle, and depends on the values of b and c.
For very small a, the upper bound on
.
However, the dependence of the eigenvalues
on a is much more subtle, and depends on the values of b and c.
For very small a, the upper bound on 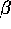 for oscillations
decreases as a increases (when
for oscillations
decreases as a increases (when 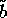 satisfies the constraint
satisfies the constraint
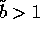 ), implying a stabilizing effect.
When the parameters are such that
), implying a stabilizing effect.
When the parameters are such that 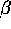 satisfies this
inequality and the value
under the square root is negative, then the real part of
satisfies this
inequality and the value
under the square root is negative, then the real part of 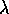 increases in magnitude with a
when 1 < b < 3, and otherwise decreases.
increases in magnitude with a
when 1 < b < 3, and otherwise decreases.
These results are found by the following calculations:
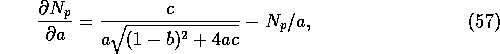
which is negative for all a>0.
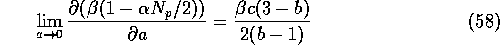
and
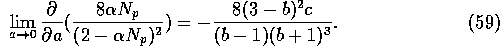



Next: References
Up: Appendix
Previous: Conditions for oscillations
weisbuch
Fri Feb 7 13:18:37 GMT+0100 1997
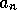 are given by equation 39 with
are given by equation 39 with 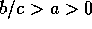 , so that prices
decrease from a maximum of
, so that prices
decrease from a maximum of 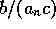 toward a minimum of
toward a minimum of 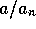 . In order to
make comparisons with the results of the other sections, a reasonable assumption is that the minimum price is
lower than under the constant price regime of section 2, i.e. that
. In order to
make comparisons with the results of the other sections, a reasonable assumption is that the minimum price is
lower than under the constant price regime of section 2, i.e. that
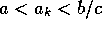 , where
, where 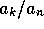 is the price of section 2. Using equation 39
implies that there is no limit on the income from selling
the harvest, as there is when a=0. However,as long as a is small
compared to 1, we expect that the results given for the a=0 case
will essentially hold: namely that a nonzero equilibrium only exists
when b is above a minimum value near
is the price of section 2. Using equation 39
implies that there is no limit on the income from selling
the harvest, as there is when a=0. However,as long as a is small
compared to 1, we expect that the results given for the a=0 case
will essentially hold: namely that a nonzero equilibrium only exists
when b is above a minimum value near 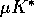 ,
and that (when
,
and that (when 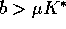 ) the
equilibrium resource level is larger,
the equilibrium is more strongly attracting,
and oscillations are less likely than in the constant price case. However,
as a moves away from zero and price supports become stronger, we would
like to know how this affects the a=0 results.
) the
equilibrium resource level is larger,
the equilibrium is more strongly attracting,
and oscillations are less likely than in the constant price case. However,
as a moves away from zero and price supports become stronger, we would
like to know how this affects the a=0 results.
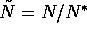 ,
, 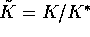 (
(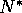 ,
, 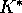 given by equation
given by equation 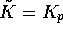 ,
, 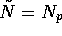 , where
, where
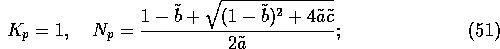
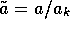 ,
,
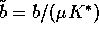
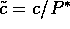 , and
, and
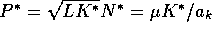 .
.
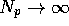 as
as 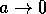 while if b>1 then
while if b>1 then 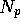 approaches the a=0
value as
approaches the a=0
value as 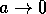 .
.
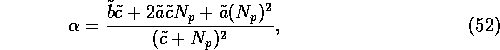
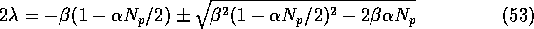
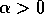 , these eigenvalues both have negative real part when
, these eigenvalues both have negative real part when
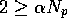 . Using the relationship between a, b, c and
. Using the relationship between a, b, c and 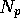 to
replace each
to
replace each 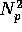 , this
condition on
, this
condition on 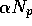 can be rewritten as
can be rewritten as
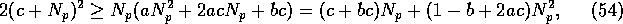
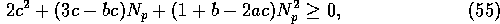
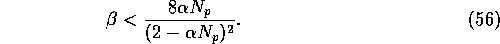
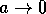 , these results approach those found in section 3.
We expect that increasing a will have the effect of 0 the impact of
decreasing prices, and, in fact, increasing
the lower bound on prices,
, these results approach those found in section 3.
We expect that increasing a will have the effect of 0 the impact of
decreasing prices, and, in fact, increasing
the lower bound on prices, 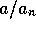 ,
decreases the equilibrium level of the resource,
,
decreases the equilibrium level of the resource, 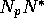 .
However, the dependence of the eigenvalues
on a is much more subtle, and depends on the values of b and c.
For very small a, the upper bound on
.
However, the dependence of the eigenvalues
on a is much more subtle, and depends on the values of b and c.
For very small a, the upper bound on 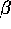 for oscillations
decreases as a increases (when
for oscillations
decreases as a increases (when 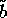 satisfies the constraint
satisfies the constraint
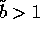 ), implying a stabilizing effect.
When the parameters are such that
), implying a stabilizing effect.
When the parameters are such that 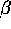 satisfies this
inequality and the value
under the square root is negative, then the real part of
satisfies this
inequality and the value
under the square root is negative, then the real part of 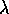 increases in magnitude with a
when 1 < b < 3, and otherwise decreases.
increases in magnitude with a
when 1 < b < 3, and otherwise decreases.