 . A more intelligent choice
for the sellers would be to monitor previous fluctuations of the number
of buyers and to decrease afternoon price in proportion.
. A more intelligent choice
for the sellers would be to monitor previous fluctuations of the number
of buyers and to decrease afternoon price in proportion.
The one-session model described in section 2 is a considerable simplification of the way buyers search for sellers. As is commonly observed in several markets with the sort of structure we are modelling here, customers that refuse a deal with one seller, usually shop around to find other offers. Indeed this is generally regarded as the principle motivation for refusal in standard search models. An alternative explanation is that customers refuse now in order to induce better offers in the future. In either case, to take this into account, we have to consider a model in which customers are given at least two occasions to purchase goods.
One further assumption to relax particularly in the case of
perishable goods is the idea of a constant price for all sessions.
In fact p is the price sellers would charge at each transaction
if they were sure to sell exactly all the quantity they bring to the
market. If they were able to predict precisely how many customers would
visit their shop and accept this price, they would know exactly how much to supply. But,
when their forecasts are not perfect
they may not have the appropriate quantity,
given the number of
possible buyers they actually face at the close of the market.
It might therefore, in this case, be better for them to sell
at a lower price
rather than to keep goods that they are not, by assumption, able to sell the
next day. We ran the
simulations with a constant afternoon price which is the morning price
lowered by a factor  . A more intelligent choice
for the sellers would be to monitor previous fluctuations of the number
of buyers and to decrease afternoon price in proportion.
. A more intelligent choice
for the sellers would be to monitor previous fluctuations of the number
of buyers and to decrease afternoon price in proportion.
To summarise then, we divide the day into two periods:
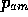 close to p. Buyers visit one shop in the morning.
close to p. Buyers visit one shop in the morning.
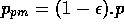 which reduces losses from unsold quantities.
Buyers visit one shop in the afternoon.
which reduces losses from unsold quantities.
Buyers visit one shop in the afternoon.
Sellers arrive in the morning with a quantity Q of the good corresponding to the number of customers they expect times q, plus some extra quantity of that good in case they have more customers than expected. The profit they expect from this additional amount is that obtained by satisfying new customers or unexpected former customers who might appear.
Buyers have to decide every morning whether to buy at the morning price or to wait for a better price in the afternoon. Of course waiting has a trade-off: they might not find anything to buy in the afternoon and thus make no profit. They choose an action according to their expectations of the average afternoon profit with respect to what they would get by buying in the morning, which they know from equation 2. Average afternoon profit is estimated from their past history of afternoon profits. We used in the simulations a simple quadratic fit of the afternoon profit as a function of morning prices. But for all reasonable choices of afternoon prices and extra supply by the sellers, expected afternoon profits for buyers are much smaller than morning profits, essentially because their chances of finding goods in the afternoon were smaller than in the morning. We discovered that even with their primitive prediction abilities, buyers soon (say after 50 time steps) realised that they would do better to accept the morning offers. For the present, we have not investigated further the issue of refusals by buyers.
Numerical simulations show that the introduction of
a second session does not change the
qualitative behaviour of the system: a low 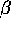 disordered regime and a
high
disordered regime and a
high 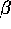 ordered regime still exist with the same
characteristics as in the one session model. But
the time to eventually reach the ordered regime and
the width of the transition are increased.
Estimated
ordered regime still exist with the same
characteristics as in the one session model. But
the time to eventually reach the ordered regime and
the width of the transition are increased.
Estimated  is 20 percent lower with two sessions than
with one.
is 20 percent lower with two sessions than
with one.
A change induced by the introduction of an
afternoon session is that divorces are
observed in the ordered regime for a much wider range
of the learning parameter  , for instance as soon as
, for instance as soon as
 is larger than 0.1 . This is because on the occasion
of an infidelity, since a buyer has a much better chance of making
a higher afternoon profit with a new shop that has extra supplies,
she then runs faster across the simplex.
is larger than 0.1 . This is because on the occasion
of an infidelity, since a buyer has a much better chance of making
a higher afternoon profit with a new shop that has extra supplies,
she then runs faster across the simplex.