 , the
probability distribution of the number of visitors, would
bring to the market a quantity n'q where n' is given by the following equation:
, the
probability distribution of the number of visitors, would
bring to the market a quantity n'q where n' is given by the following equation:
We previously mentionned that the sellers should adjust the
quantities brought to the market every morning to take into
account the expected number of customers, including eventually
fluctuations. In order to optimise the next day's profit,
a seller with
a perfect knowledge of  , the
probability distribution of the number of visitors, would
bring to the market a quantity n'q where n' is given by the following equation:
, the
probability distribution of the number of visitors, would
bring to the market a quantity n'q where n' is given by the following equation:

The above expression is optimal for one day, but does not take into account future gains that could be obtained by systematically bringing extras to make unexpected customers loyal.
Anyway, we did not suppose for the simulations that sellers have a perfect knowledge of the probability distribution of visitors, but that they use a simple routine to add extra whenever they observe fluctuations in the number of visits. The extra at time t is computed according to

where  is small and
is small and  is the variance of
the number of buyers computed from the beginning of the simulation. The
initial value of
is the variance of
the number of buyers computed from the beginning of the simulation. The
initial value of 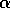 is non zero at the beginning of the simulation.
We checked by several numerical simulations with different choices
of initial
is non zero at the beginning of the simulation.
We checked by several numerical simulations with different choices
of initial  and of
and of  that the only observable changes
were variations of
that the only observable changes
were variations of  , the critical threshold for order, in the ten percent range
. The existence of two dynamical regimes persists.
, the critical threshold for order, in the ten percent range
. The existence of two dynamical regimes persists.
Another possible refinement would consist in improving the predictive
ability of the seller with respect to the number of customers.
We tried a moving average prediction rather than the prediction
based only on the preceeding day but this only downgraded performance
( increases).
increases).