


Next: Mean Field Approach
Up: The simplest Model
Previous: Prices and quantities
Now that we have specified how quantities and prices are determined, what happens
in the market depends on the actual visits of buyers to sellers:
sellers are chosen by buyers according to certain probabilities.
The latter are derived from " preference coefficients " which are
built upon the history of each buyer's past profits with each seller.
The learning and probabilistic choice processes to be described in this
section are the "invariant core" of the model. They are largely inspired
from the formal neural networks
approach to reinforcement learning as described for instance
in Weisbuch (1990).
They will not be modified in any of the subsequent versions of the model
(which is not the case for the simple rules for choosing price
and quantities described above).
Let first specify the learning process of the buyers. By assumption
the only information available to them come from previous
transactions. We first propose to map that information into
preference coefficients 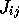 of buyer i for seller j. These
are constructed by recording the profits that buyer i made
from his previous transaction with seller j. At
the same time these previous profits are discounted at a constant rate
of buyer i for seller j. These
are constructed by recording the profits that buyer i made
from his previous transaction with seller j. At
the same time these previous profits are discounted at a constant rate
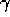 . Since we use discrete time
for transactions, preferences are updated at each time step
according to:
. Since we use discrete time
for transactions, preferences are updated at each time step
according to:

In other words, at each time step, all preferences coefficients are discounted at a
constant rate, while the preference coefficient for the shop with which
a transaction occurs is increased by the profit made in that shop.
Discounting previous profits at a constant rate is important
in ensuring that information is relevant to the current
situation: in general, shops do not have stationary
characteristics in terms of the profits that they offer because of
changes in prices or the level of their supply with respect
to the number of customers they have to serve. Preference coefficents
thus appear as the sum of discounted past profits.
Buyers then use these preference coefficents to choose a shop.
One way to do so
is to choose the shop with the best record, that is the
shop with the highest 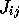 . However, by always doing this, the buyer will become
a captive of the selected shop which would then be in a position
to increase its prices, thus diminishing the buyer's profit.
The shop can do this until the buyer's profit becomes negative
before running any risk of losing that buyer.
It is therefore in the buyer's interest to search from time to time among other sellers
to check whether he could get a better profit elsewhere. In other words,
a good strategy for the buyers would be a balance between
the deterministic choice
in favor of those shops which gave the best profits in the
past and random search among other sellers. This raises
the well known issue of the trade-off between exploitation of old knowledge
and exploration to acquire new knowledge. We suppose here
that a buyer chooses a shop j with a probability
. However, by always doing this, the buyer will become
a captive of the selected shop which would then be in a position
to increase its prices, thus diminishing the buyer's profit.
The shop can do this until the buyer's profit becomes negative
before running any risk of losing that buyer.
It is therefore in the buyer's interest to search from time to time among other sellers
to check whether he could get a better profit elsewhere. In other words,
a good strategy for the buyers would be a balance between
the deterministic choice
in favor of those shops which gave the best profits in the
past and random search among other sellers. This raises
the well known issue of the trade-off between exploitation of old knowledge
and exploration to acquire new knowledge. We suppose here
that a buyer chooses a shop j with a probability 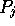 which is proportional
to the exponential of the preference coefficient for that shop. That is:
which is proportional
to the exponential of the preference coefficient for that shop. That is:
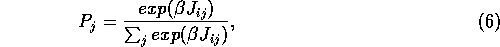
where 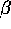 measures the non-linearity of the relationship between the
probability
measures the non-linearity of the relationship between the
probability 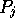 and the preference coefficient
and the preference coefficient 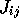 .
.
The exponential rule has been widely used in economics
and elsewhere. In particular, several justifications
for its use are given in the discrete choice literature, see e.g.
Anderson et al. (1992).
In our case, the exponential rule
can be derived directly. This is done by maximizing the weighted sum F of two terms, one of
which favors immediate profit and the other which favors search.
To maximise information gain during visits, buyers should
maximize the Shannon entropy of the distribution of search probabilities:

The function F to be maximized is then a linear combination of
preferences and entropy terms:
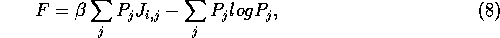
Setting the derivatives with respect to 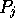 equal to zero under the constraint that the sum
of the probabilities is 1 gives equation 6.
equal to zero under the constraint that the sum
of the probabilities is 1 gives equation 6. 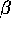 is then simply interpreted as the relative weight of the discounted sum of
profits with respect to the amount of information in function F.
is then simply interpreted as the relative weight of the discounted sum of
profits with respect to the amount of information in function F.



Next: Mean Field Approach
Up: The simplest Model
Previous: Prices and quantities
weisbuch
Mon Feb 10 13:26:18 GMT+0100 1997
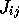 of buyer i for seller j. These
are constructed by recording the profits that buyer i made
from his previous transaction with seller j. At
the same time these previous profits are discounted at a constant rate
of buyer i for seller j. These
are constructed by recording the profits that buyer i made
from his previous transaction with seller j. At
the same time these previous profits are discounted at a constant rate
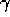 . Since we use discrete time
for transactions, preferences are updated at each time step
according to:
. Since we use discrete time
for transactions, preferences are updated at each time step
according to:

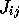 . However, by always doing this, the buyer will become
a captive of the selected shop which would then be in a position
to increase its prices, thus diminishing the buyer's profit.
The shop can do this until the buyer's profit becomes negative
before running any risk of losing that buyer.
It is therefore in the buyer's interest to search from time to time among other sellers
to check whether he could get a better profit elsewhere. In other words,
a good strategy for the buyers would be a balance between
the deterministic choice
in favor of those shops which gave the best profits in the
past and random search among other sellers. This raises
the well known issue of the trade-off between exploitation of old knowledge
and exploration to acquire new knowledge. We suppose here
that a buyer chooses a shop j with a probability
. However, by always doing this, the buyer will become
a captive of the selected shop which would then be in a position
to increase its prices, thus diminishing the buyer's profit.
The shop can do this until the buyer's profit becomes negative
before running any risk of losing that buyer.
It is therefore in the buyer's interest to search from time to time among other sellers
to check whether he could get a better profit elsewhere. In other words,
a good strategy for the buyers would be a balance between
the deterministic choice
in favor of those shops which gave the best profits in the
past and random search among other sellers. This raises
the well known issue of the trade-off between exploitation of old knowledge
and exploration to acquire new knowledge. We suppose here
that a buyer chooses a shop j with a probability 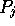 which is proportional
to the exponential of the preference coefficient for that shop. That is:
which is proportional
to the exponential of the preference coefficient for that shop. That is:
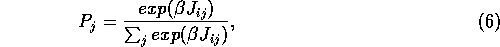
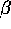 measures the non-linearity of the relationship between the
probability
measures the non-linearity of the relationship between the
probability 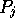 and the preference coefficient
and the preference coefficient 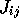 .
.

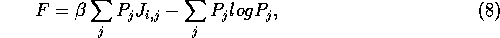
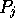 equal to zero under the constraint that the sum
of the probabilities is 1 gives equation
equal to zero under the constraint that the sum
of the probabilities is 1 gives equation 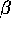 is then simply interpreted as the relative weight of the discounted sum of
profits with respect to the amount of information in function F.
is then simply interpreted as the relative weight of the discounted sum of
profits with respect to the amount of information in function F.