From Werner KRAUTH
Werner Krauth
Laboratoire de Physique Statistique
École normale supérieure
24 rue Lhomond
75231 Paris Cedex 05
France
Tel +33 (0)1 44 32 25 50
werner.krauth@ens.fr
CNRS Research Director (Theoretical Physics)
Director of the Physics Departement at Ecole normale supérieure, Paris, France (since January 2010);
Director of the LabEx ENS-ICFP ( ENS-International Center for fundamental physics and its interfaces).
Current research
I am deeply interested in statistical physics and condensed matter physics, often in connection to computation and algorithms.
Current interests are in hard spheres, mainly the melting transition in two-dimensional disks, bosons (in collaboration with the experimental groups at ENS), and the theory of convergence and of coupling in Markov chains.
By the way: the term
melting of hard disks does not relate to the irreversible memory loss when your laptop catches fire (left figure), but to a fundamental phase transition in the model of two-dimensional hard spheres, that is, billiard balls without friction and without inner structure (center and right figures). The possibility that two-dimensional systems with continuous degrees of freedom could melt was discovered in 1962, by Alder and Wainwright, but the nature of the transition remained a mystery for several decades (
but we think we now solved it).
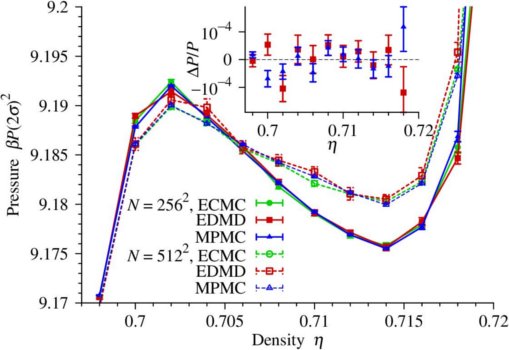
Hard-disk equation of state: First-order liquid-hexatic transition in two dimensions with three simulation methods
Spring and summer of 2012 was partly spent on a project with colleagues Joshua Anderson, Michael Engel and Sharon Glotzer from the University of Michigan, Masaharu Isobe from the Nagoya Institute of Technology, and Etienne Bernard from MIT. We were interested in checking
our earlier results on the melting transition of hard disks in two dimensions which predicted the existence of a first-order liquid-hexatic phase transition - a big surprise after hundreds of other papers had fought over two other scenarios for melting in two dimensions.
Our confirmation preprint finally came out in November 2012. Using three completely independent algorithms (
massively parallel local Monte Carlo, molecular dynamics,
event-chain Monte Carlo), we confirmed our earlier data (see figure to the left). We are all happy about this independent verification, and Etienne Bernard and I are quite relieved, as so much can go wrong with numerical simulations, especially if they take an eternity, almost, to run.
The figure to the left shows the equation of state for hard disks (the equilibrium pressure as a function of the density (or the volume), with the characteristic loop which indicates the presence of two phases - a minority phase that forms a bubble inside the majority phase. The inset gives the difference between the old data (from last year) and the new ones. Let me note that, if the simulation is nontrivial, the calculation of the pressure is quite tricky also, especially in Monte Carlo calculations, as an extrapolation of the pair-correlation function is involved. Those of us in the team who did Monte Carlo evaluation were much relieved to see the nice agreement with the molecular dynamics results, obtained with Masaharu Isobe's code, where the pressure is computed simply by counting the number of collisions taking place over a months-long simulation. For more details, see the
preprint.
Event-driven Monte Carlo algorithm for general potentials
In recent works, as for example on the melting transition in two dimensions, the event-chain algorithm has proven quite helpful. This hard-sphere Monte Carlo method runs a lot faster than earlier methods although the speed-uo remains constant for large system sizes. Nevertheless, gaining a factor of about 100 is not so bad for run-times (with the new algorithm) on the order of a few months... we got our results before it was time to retire.
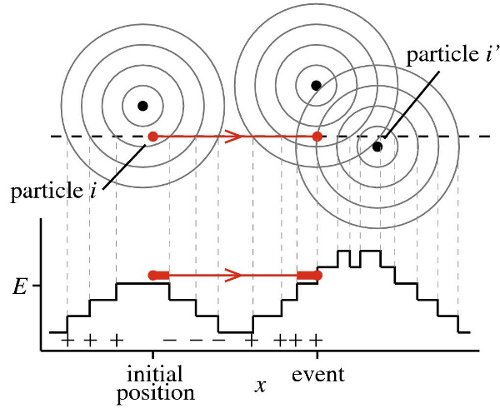
Recently, in 2012, Etienne Bernard (now at MIT) and I were able to
extend the event-chain algorithm to continuous potentials, and we are now quite excited: The algorithm allows to break detailed balance, it is (hopefully) much faster than local Monte Carlo algorithms, and it is extremely easy to program, to parallelize (hopefully), to modify and, why not, to improve. Technically, we work with stepped potentials (see the figure, similar approaches exist for molecular dynamics), but there is no problem going to finer and finer discretizations: the algorithm doesn't even slow down as we crank up the number of steps. This is explained
in a section of the wiki page dedicated to our recent paper. But lots of things need to be done to understand this new approach, to check out possible applications, etc, and we are right now extremely busy.
Two-dimensional melting: First-order liquid-hexatic transition
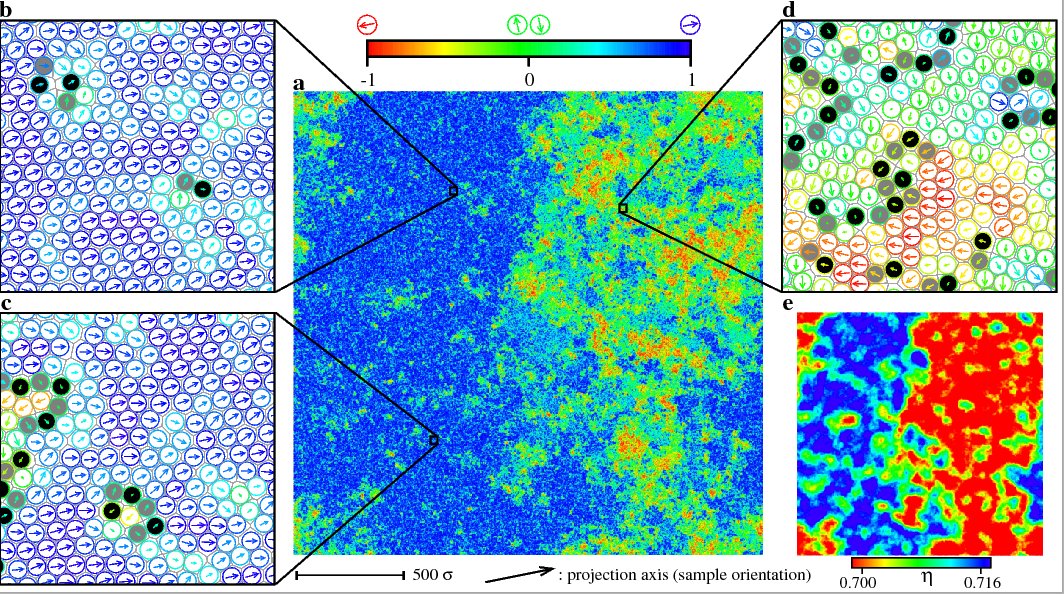
Here, I show the key figure of
a recent paper, from 2011, with Etienne Bernard, on the melting transition in hard disks. The main picture shows the orientations of a configuration with 1024x1024 disks, and two different regions are clearly visible: To the left, disks have more or less the same orientation, whereas to the right, the orientations vary (and the local densities are lower). This clearly indicates the presence of a first-order transition (for details see the paper). In our paper, we show not only that the transition is of first order, but also that it is between the liquid and a hexatic phase. Our melting scenario differs from what hundreds of earlier papers seemed to indicate, namely that the two-dimensional melting transition either followed the famous KTHNY scenario or was a direct transition from the liquid to the solid state, as in three dimensions. The fight for truth between these two groups raged for several decades. Using much better simulation methods, we could show that both were off, and the scenario adopted by nature is not what was imagined for so long.
To produce the picture, we used the
event-chain algorithm, a Monte Carlo method that we developed a few years ago, with David Wilson. This algorithm is really the first one to outperform, by about two orders of magnitude in speed, the classic Metropolis method from 1953. For a long time, I have been interested in the hard-disk melting problem, but an earlier attempt to speed up the extremely slow converge of numerical methods for this problem, the cluster algorithm that I developed with C. Dress, had failed.
Upcoming events
Berkeley Mini Stat Mech Meeting 11 - 13 January 2013, Berkeley, CA, USA (Invited talk)
Statphys25, July 22 – 26, 2013, Seoul National University, Seoul, Korea (Invited talk)
Here is the schedule of past events
Text book
A picture book of algorithms
Direct-sampling algorithm for ideal bosons in a trap (see
article with M. Holzmann). Adapted for interacting bosons, this algorithm was used in a variety of articles.
Alder and Wainwright's event-driven Molecular Dynamics algorithm (1957). (Animation by Maxim Berman).
