Since the oscillations around equilibrium are the major features of the dynamics of this model, let us discuss here their condition of existence in the same class of models. As shown by the same linear analysis, if we consider a generalized Cobb-Douglas function with elasticities u, v and w different from 0.5 or 1 such as:
the real part of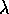 
is :
The stability of the limit point is maintained as long as
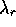is negative. For constant catch per unit effort (w=1)
this is true when u is smaller than one, which corresponds to decreasing returns in capital.
However, instabilities could occur because of decreasing returns with respect
to the stock of fish (w<1), when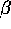 
is small. Some
observations of [Opsomer and Conrad, 1994] on anchovy fisheries, with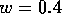 
correspond to this latter case.
In order to test the generic character of oscillation dynamics
let us take a very general production function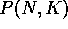 
and perform
the linear stability analysis with respect to 
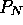and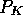 
, the formal derivatives of
P with respect to N and K.
One then obtains the following system of equations in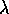 
:
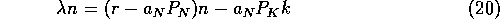
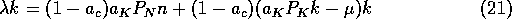
where n and k are the deviations of N and K from their equilibrium values.
In any two equation differential system, as shown in the appendix, linear stability analysis shows that oscillations, implying here overshoot and depletion, are to be expected whenever:
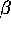. We will further discuss
possible saturations effects, due to carrying capacity or price
dynamics, which may decrease 
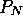or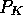 
and thus limit the range of existence of oscillations.
