


Next: Carrying capacity
Up: The simplest model:
Previous: More general production
Let us come back to the nondimensionalized system in order to interpret these
results. The unstable equilibria are never reached and are of little interest.
Let us focus on the stable equilibrium and
on the evolution towards equilibrium.
The equilibrium
resource size 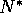 increases with the renewal rate of the resource r, the
capital depreciation rate
increases with the renewal rate of the resource r, the
capital depreciation rate 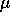 , and decreases
with the rate of production
, and decreases
with the rate of production 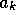 ,
the efficiency of the harvesting
,
the efficiency of the harvesting 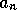 and the amount of people involved
in the harvest, L (equation 5). The fact that the equilibrium
capital
and the amount of people involved
in the harvest, L (equation 5). The fact that the equilibrium
capital 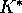 is inversely proportional to L simply reflects
the replacement of capital by labour in the Cobb-Douglas expression
1.
is inversely proportional to L simply reflects
the replacement of capital by labour in the Cobb-Douglas expression
1. 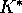 also increases with r and decreases with
also increases with r and decreases with 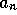 .
.
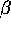 is small, giving rise to oscillations,
whenever resource renewal is fast with
respect to capital depreciation, which is probably the case
for most fisheries. The resource renewal rate for most species of fish
is of the order of a few years, while boats last for a couple of decades at least (major pieces of fishing gear typically last for seven years).
The situation for forest exploitation might be the
opposite, with
is small, giving rise to oscillations,
whenever resource renewal is fast with
respect to capital depreciation, which is probably the case
for most fisheries. The resource renewal rate for most species of fish
is of the order of a few years, while boats last for a couple of decades at least (major pieces of fishing gear typically last for seven years).
The situation for forest exploitation might be the
opposite, with 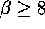 and no oscillations and a fast decay
towards equilibrium.
and no oscillations and a fast decay
towards equilibrium.
An important result is that
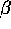 is independent of the production coefficients
is independent of the production coefficients
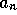 and
and 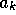 :
: 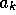 can be increased by
technological or marketing
improvements that decrease the quantity of a natural
resource used in a given product. This would not change the oscillatory
nature of the solutions. In the case of forest exploitation
such an improvement might be using less wood for a given piece of furniture
or making use of a larger proportion of each tree; for fisheries
it might be practices enabling the industry to use a larger fraction
of the catch by marketing surimi or flour for cattle breeding.
On the other hand, such practices can improve the situation by increasing
the equilibrium resource size, which is a good
defense against natural or artificial hazards which could suddenly
deplete the resource below the threshold level necessary for reproduction.
can be increased by
technological or marketing
improvements that decrease the quantity of a natural
resource used in a given product. This would not change the oscillatory
nature of the solutions. In the case of forest exploitation
such an improvement might be using less wood for a given piece of furniture
or making use of a larger proportion of each tree; for fisheries
it might be practices enabling the industry to use a larger fraction
of the catch by marketing surimi or flour for cattle breeding.
On the other hand, such practices can improve the situation by increasing
the equilibrium resource size, which is a good
defense against natural or artificial hazards which could suddenly
deplete the resource below the threshold level necessary for reproduction.



Next: Carrying capacity
Up: The simplest model:
Previous: More general production
weisbuch
Fri Feb 7 13:18:37 GMT+0100 1997
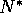 increases with the renewal rate of the resource r, the
capital depreciation rate
increases with the renewal rate of the resource r, the
capital depreciation rate 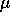 , and decreases
with the rate of production
, and decreases
with the rate of production 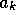 ,
the efficiency of the harvesting
,
the efficiency of the harvesting 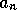 and the amount of people involved
in the harvest, L (equation 5). The fact that the equilibrium
capital
and the amount of people involved
in the harvest, L (equation 5). The fact that the equilibrium
capital 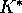 is inversely proportional to L simply reflects
the replacement of capital by labour in the Cobb-Douglas expression
1.
is inversely proportional to L simply reflects
the replacement of capital by labour in the Cobb-Douglas expression
1. 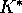 also increases with r and decreases with
also increases with r and decreases with 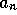 .
.
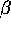 is small, giving rise to oscillations,
whenever resource renewal is fast with
respect to capital depreciation, which is probably the case
for most fisheries. The resource renewal rate for most species of fish
is of the order of a few years, while boats last for a couple of decades at least (major pieces of fishing gear typically last for seven years).
The situation for forest exploitation might be the
opposite, with
is small, giving rise to oscillations,
whenever resource renewal is fast with
respect to capital depreciation, which is probably the case
for most fisheries. The resource renewal rate for most species of fish
is of the order of a few years, while boats last for a couple of decades at least (major pieces of fishing gear typically last for seven years).
The situation for forest exploitation might be the
opposite, with 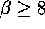 and no oscillations and a fast decay
towards equilibrium.
and no oscillations and a fast decay
towards equilibrium.
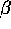 is independent of the production coefficients
is independent of the production coefficients
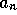 and
and 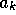 :
: 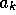 can be increased by
technological or marketing
improvements that decrease the quantity of a natural
resource used in a given product. This would not change the oscillatory
nature of the solutions. In the case of forest exploitation
such an improvement might be using less wood for a given piece of furniture
or making use of a larger proportion of each tree; for fisheries
it might be practices enabling the industry to use a larger fraction
of the catch by marketing surimi or flour for cattle breeding.
On the other hand, such practices can improve the situation by increasing
the equilibrium resource size, which is a good
defense against natural or artificial hazards which could suddenly
deplete the resource below the threshold level necessary for reproduction.
can be increased by
technological or marketing
improvements that decrease the quantity of a natural
resource used in a given product. This would not change the oscillatory
nature of the solutions. In the case of forest exploitation
such an improvement might be using less wood for a given piece of furniture
or making use of a larger proportion of each tree; for fisheries
it might be practices enabling the industry to use a larger fraction
of the catch by marketing surimi or flour for cattle breeding.
On the other hand, such practices can improve the situation by increasing
the equilibrium resource size, which is a good
defense against natural or artificial hazards which could suddenly
deplete the resource below the threshold level necessary for reproduction.