PastResearchNotices

From Werner KRAUTH

Return to the "Current Research" section

Contents 1 Event-Chain Monte Carlo: Foundations, Applications, and Prospects 2 Fast sequential Markov chains 3 Multithreaded event-chain Monte Carlo with local times 4 JeLLyFysh-Version1.0 -- a Python application for all-atom event-chain Monte Carlo 5 All-atom Coulomb simulations with irreversible Markov chains 6 Thermodynamic phases in two-dimensional active matter 7 Irreversible local Markov chains with rapid convergence towards equilibrium 8 Cell-veto Monte Carlo algorithm for long-range systems 9 Event-chain algorithm for continuous spin systems: XY & Heisenberg models, spin glasses 10 Soft-disk melting: From liquid-hexatic coexistence to continuous transitions 11 Efimov-driven phase transitions of the unitary Bose gas 12 Generalized event-chain Monte Carlo: Rejection-free global-balance algorithms from infinitesimal steps 13 Sampling from a polytope and hard-disk Monte Carlo 14 Hard-disk equation of state: First-order liquid-hexatic transition in two dimensions with three simulation methods 15 Event-driven Monte Carlo algorithm for general potentials 16 Two-dimensional melting: First-order liquid-hexatic transition

Event-Chain Monte Carlo: Foundations, Applications, and Prospects

In the last decade, I've been very interested in non-reversible Markov chains, and in the event-chain Monte Carlo. What started (for us) as an ad-hoc Monte Carlo algorithm for hard spheres has morphed into a general method, with the conceptual underpinnings coming out clearer with time. In June 2021, my review Event-Chain Monte Carlo: Foundations, Applications, and Prospects was published in Frontiers in Physics. Access is open.

Fast sequential Markov chains

As many people know, the Markov-chain Monte Carlo method in the form of the Metropolis algorithm for reversible Markov chains, was discovered in 1953, by Metropolis, Rosenbluth, Rosenbluth (sic), Teller, and Teller (sic) in a landmark paper. But the authors not only discovered reversible Markov chains, they also implemented the first non-reversible Markov chain! The difference may be a bit difficult to understand here, on a website, but for a reversible Markov chain a move and its inverse must always be likely. This is realized if, in a system of N particles, at each time step, one picks a random particle and moves it through a random displacement (see my book for an explanation). But Metropolis et al. didn't implement it this way: At time 1, they moved particle 1, then at time 2, they moved particle 2, and so on until, at time N+1, the first particle is moved again. This is manifestly non-reversible, but still samples the Boltzmann distribution. In later research, over the decades, it was found that whether one uses the sequential algorithm or chooses particles randomly doesn't make a great deal of a difference. No big deal!

In June 2020, Liang Qin (Laboratoire de Physique, ENS), Philippe Hoellmer (University of Bonn) and I looked into a variant of the sequential Markov chain algorithm, but instead of going sequentially through particle indices, we go sequentially through the directions. In practice, all particles first move (for a long time) along the x-axis, then with an inclination of 1 degree, then 2 degrees, etc (see the above figure). We studied this not for hard disks (as Metropolis et al in 1953), but a simple model of an elastic dipole. What we found was really surprising: By sequentially going through the directions, one induces very persistent counter-clockwise rotation but then, after a while, another very persistent clockwise rotation follows. We were able to prove rigorously that if we replace the 1 degree change by an angle Delta Phi, then in the limit of small Delta Phi, the rolled-out angle diverges! However, we could also prove that the net rotation of the clockwise and counter-clockwise rotations adds up to exactly zero. Finally, we showed numerically that the sequential Markov-chain algorithm is much faster than what we did before. The story is told in this paper.

Multithreaded event-chain Monte Carlo with local times

In the last few years, our delocalized group has worked on a new paradigm of Markov-chain Monte Carlo methods that break detailed balance yet sample the equilibrium Boltzmann distribution. The algorithms go by the name of 'event-chain Monte Carlo', and as the name indicates, they are event-driven (this means: they hop from event to event, rather than from femto-second timestamp to femto-second timestamp). One of the problem of event-driven algorithms is that they were never successfully parallelized. Looking at today's computer architectures, which are massively parallel (either on GPUs or on shared-memory CPUs), this long provided a bleak outlook for the practical applications of ECMC.

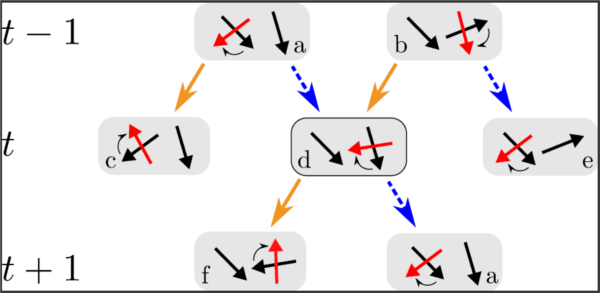
However, in a paper that recently appeared in Computer Physics Communications, Botao Li (from ENS), Synge Todo (from University of Tokyo), A. C. Maggs (from ESCPI Paris) and myself were able to present a multithreaded event-chain Monte Carlo algorithm for hard spheres. Threads synchronize at infrequent breakpoints and otherwise scan for local horizon violations. On x86 and ARM processors, a C++ (OpenMP) implementation that uses compare-and-swap primitives for data access achieves considerable speed-up with respect to single-threaded code. The paper appeared in a computer physics journal, and there is a lot of computer-nerdy content in it (everything is open-source and all our C++ and Python programs are open-source and available on github) . However, there is also a lot of math in the paper, including real lemmas and their proofs, which at the beginning were not at all clear to us. We present a total of six algorithm (the final one goes really fast), and one of them (Algorithm 5) is rigorously proven to be without bugs, as we can map it onto an absorbing Markov chain with 3670 states, that we can analyze exactly (the picture gives a visual impression of the proof).

PS: This is the first paper of Botao Li, first-year (now second-year) graduate student at ENS, and we are all very happy.

JeLLyFysh-Version1.0 -- a Python application for all-atom event-chain Monte Carlo

For the last few years, the development of irreversible-Markov-chain methods for physics applications has been at a focus of our group's interest. Although we have constantly thought about algorithms (in particular about the event-chain algorithm), no general code was available. This changed during the week of 29 July 2019 where, on Monday, we posted a 50-page manuscript, that has since been accepted by Computer Physics Communications, and on Thursday (1 August 2019), when we pushed to first Version of the associated open-source Python application to GitHub (see https://github.com/jellyfysh, some 15,000 lines of Python3 code). Both works are authored by Philipp Höllmer, Liang Qin, Michael F. Faulkner, A. C. Maggs, and me, and we are all quite proud to have finished. The code is 100% open access (it suffices to go onto the GitHub website and to fork it by clicking on a button). By the way, the program's name is JeLLyFysh (because we think that it will be very helpful to treat systems mostly with water, and some other stuff).

All-atom Coulomb simulations with irreversible Markov chains

In a nutshell, classical molecular-dynamics simulations consist in computing the forces on particles, at discretized time steps, and in moving these particles in accordance with Newton's law of motion, the famous F=ma. Likewise (in a nutshell), classical Monte Carlo calculations consist in proposing a move, then in computing the change of the total system energy, and then accepting or rejecting the move with a probability given by the Metropolis filter. How to compute the forces (for molecular dynamics) or the energies (for Monte Carlo) is a science in its own right, whenever the interactions are long-ranged, as for the Coulomb potential. Much used elaborate methods go by the names of PP (for particle-particle) or PPPM (for particle-particle / particle-mesh), or else particle-mesh Ewald etc. They have in common that much ingenuity is applied to compute a quantity (force / energy) that, as we claimed a few years ago, is not needed to drive the system forward! For a recent article in Journal of Chemical Physics, I teamed up with Michael Faulkner, Liang Qin, and Anthony C. Maggs, to show how this can be done in practice. In what, internally, we call our 'Proof-of-Concept paper', we explicitly show how to set up a highly efficient algorithm to simulate a model of liquid water. We indeed confirm that it is possible to sample the Boltzmann distribution (which involves the Boltzmann weight, and therefore the system energy), without computing the energy. As often, the difference lies in the subtle difference between the concepts of 'sampling' (that is, obtaining examples of a certain distribution) and of 'computing' (for example computing the energy). Technically, we succeed in drawing independent samples with a complexity 'N' log 'N' (just like the best PPPM algorithms but, we think, much faster). Now, of course, after the first excitement of our 'confirmation paper', we are all excited by the forthcoming 'benchmark paper', where we will compare not only complexities, but actual running times.

Thermodynamic phases in two-dimensional active matter

Active matter (for example the collective dynamics of flocks of birds, of schools of fish, etc) is a very active field of research in statistical physics. However, active matter cannot really be described by equilibrium statistical theory where the state of what is called the system is fully characterized by two numbers (for example the volume and the pressure), and where the statistical weight of each configuration can be attributed an energy E, and a statistical Boltzmann weight exp(-beta E) which depends on the energy alone. Many active materials are two-dimensional (ranging from sheep on a meadow to bacterial colonies to artificial Janus particles on a glass place. As we are so much interested in regular two-dimensional particle systems (that are described by equilibrium statistical physics), we posed the question of whether there was some kind of continuous passage between the two types of models. Teaming up with Juliane U. Klamser and Sebastian C. Kapfer, we studied this question in detail. Our conclusions were published, in November 2018, in Nature Communications.

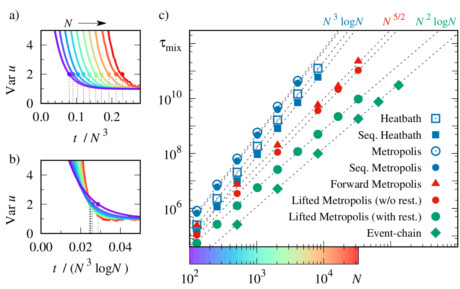
Irreversible local Markov chains with rapid convergence towards equilibrium

Monte Carlo algorithms, generally satisfy the detailed balance condition, which prescribes that in the limit of infinite times, the probability flow from a configuration a to a configuration b equals the flow from b to a. This may seem terrible abstract, but it simply means that if, in a room full of air molecules, each molecule moves to the left and to the right with the same probability (and sometimes does not move at all, because there is already another particle where it wants to go), the density of air will be more or less uniform. In a recent paper with Sebastian Kapfer, in Physical Review Letters, we systematically studied irreversible local Markov chain, that is, Monte Carlo algorithms which only satisfy the global balance condition, but not the detailed balance (in the example of the air-filled room, this corresponds to algorithms where the molecules are much more likely to move in one direction than the other, but where the asymptotic density is still uniform). We considered the case of hard-sphere gases in one spatial dimension with periodic boundary conditions and, to our greatest surprise, came up with Markov chains such as the 'forward Metropolis algorithm' or the 'lifted forward Metropolis algorithm', or even the 'lifted forward Metropolis algorithm with restart' that mix much faster than the usual methods, although they reach exactly the same steady state in the limit of infinite times. We even made contact with the vast research literature on the TASEP (totally asymmetric simple exclusion process), a discrete variant of our Markov chains. We are all the more excited that the algorithms studied are but special versions of the event-chain algorithm, that we used a lot during the last years.

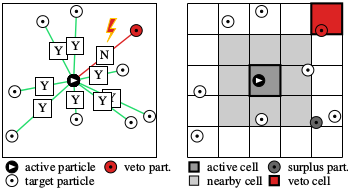
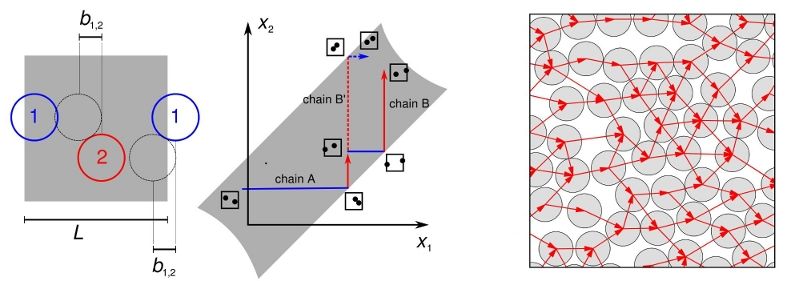
Cell-veto Monte Carlo algorithm for long-range systems

In a recent paper, together with Sebastian Kapfer, we have presented what we think might be a new start idea for the notoriously difficult simulation of long-ranged systems (such as the Coulomb 1/r interaction). Usually it poses problems, because the evaluation of the energy is so difficult: In a long-ranged system of N particles, the interactions are basically of everybody with everybody else. This makes that the evaluation of the energy becomes complicated, and the energy is needed in 99.99% of all simulation algorithms (Monte Carlo or Molecular dynamics). In our new algorithm (an application of the event-chain method), one does not compute the system energy in order to decide on a change of the physical system, but rather looks at all the interactions separately. So, if a particle a (the active particle) wants to move, it has to ask all its partners t_1, t_2, .... (the target particles). If there is only a single veto, the move is rejected. In the cell-veto algorithm (see the right side of the figure), the identification of the rejecting particle is preceeded by that of a veto cell. The advantage of this is that cell vetos can be identified immediately (in a constant number of operations, that is, in O(1)), and then instantly confirmed or infirmed on the particle level.

Event-chain algorithm for continuous spin systems: XY & Heisenberg models, spin glasses

In past years, several of our key results, for example about two-dimensional melting for hard disks but also the melting scenario for soft-disk systems, have relied on the new event-chain algorithm, that applies to both systems, hard-core and soft-core. More recently, we realized that the event-chain algorithm could also be made to work for continuum spin systems. Earlier in 2015, work started with Manon Michel and Johannes Maier, PhD candidate and ENS-ICFP master student, respectively. The first simulations were followed by a period of hectic activity: We had discovered that the event-chain algorithm was about 100 times faster that the local Monte Carlo algorithm. Our findings were written up, during the month of August 2015, in a manuscript entitled Event-chain Monte Carlo for classical continuous spin models. Only six weeks later (!), Manon Michel and I submitted another manuscript, together with our colleagues Yoshihiko Nishikawa and Koji Hukushima, from the University of Tokyo, entitled Event-chain algorithm for the Heisenberg model: Evidence for z ≃ 1 dynamic scaling. This new finding (that still awaits confirmation for larger systems than the ones we could simulate quickly), has had an electrifying effect on us: For the first time, we see the kind of maximum speed-up that can be realized by irreversible Markov chains using the lifting paradigm, if we suppose that the recent mathematical theories apply to the algorithms we have been developing. Of course, we now hope to find the z=1 scaling in Heisenberg spin glasses and related systems and, why not, in the original hard-sphere models, in two dimensions as well as in three.

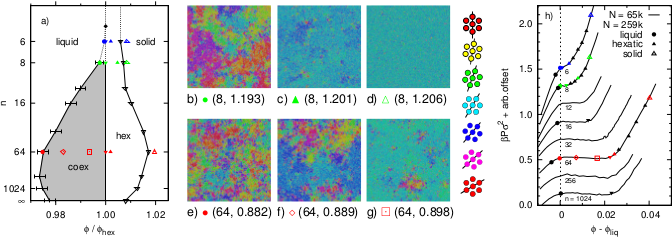
Soft-disk melting: From liquid-hexatic coexistence to continuous transitions

By the way: the term melting of hard disks does not relate to the irreversible memory loss when your computer hard disk catches fire (left figure), but to a fundamental phase transition in the model of two-dimensional hard spheres, that is, billiard balls without friction and without inner structure (center and right figures). The possibility that two-dimensional systems with continuous degrees of freedom could melt was discovered in 1962, by Alder and Wainwright, but the nature of the transition remained a mystery for several decades (until we solved it).

In a recent paper with Sebastian Kapfer, in Physical Review Letters (2015), we discuss phase transitions in two-dimensional socalled soft-disk systems with repulsive power-law pair interactions ∝r^(−n), using the recent generalization of Event-Chain Monte Carlo to continuous potentials. The recently established melting scenario for hard disks (corresponding to n=∞) is preserved for finite n, and first-order liquid-hexatic and continuous hexatic-solid transitions are identified. The density difference between the coexisting hexatic and liquid is non-monotonous as a function of n. For smaller n, the coexisting liquid shows extremely long orientational correlations, and positional correlations in the hexatic become extremely short. For n≲6, the liquid-hexatic transition is continuous, with correlations consistent with the KTHNY scenario.

The graph on the left provides the main result of our paper (x-axis: density/ pure hexatic; y-axis: power n): We see a large region with liquid-hexatic coexistence.

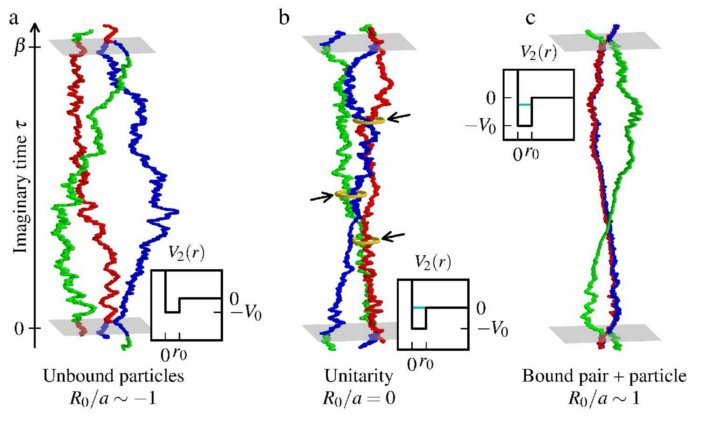
Efimov-driven phase transitions of the unitary Bose gas

In a recent article with Swann Piatecki, published in Nature Communications 5, 3503 (2014), we discuss Efimov trimers: bound configurations of three quantum particles that fall apart when any one of them is removed. They open a window into a rich quantum world that has become the focus of intense experimental and theoretical research, as the region of ‘unitary’ interactions, where Efimov trimers form, is now accessible in cold-atom experiments. We use a path-integral Monte Carlo algorithm backed up by theoretical arguments to show that unitary bosons undergo a first-order phase transition from a normal gas to a superfluid Efimov liquid, bound by the same effects as Efimov trimers. A triple point separates these two phases and another superfluid phase, the conventional Bose–Einstein condensate, whose coexistence line with the Efimov liquid ends in a critical point. We discuss the prospects of observing the proposed phase transitions in cold-atom systems.

Here you see three bosons, in path integral representation, and with a certain pseudopotential interaction that is described in more detail in the paper. On the left side, the particles are slightly repulsive, on the right side, they are attractive (so that two particles simple get together and bind into a dimer, whereas the third particle just sits around. In the center, you see the particles at the unitary point: pair interactions are very weak, so pairs get together, but unbind. After a little while, another pair forms, etc etc. The final outcome is that ensembles of two particles fall apart, but three particles stay together, just like Borromean rings...

Generalized event-chain Monte Carlo: Rejection-free global-balance algorithms from infinitesimal steps

Our 2009 event-chain algorithm for hard spheres, with Etienne Bernard and David Wilson, is a new paradigm for Monte Carlo simulations. For a while, it was unclear whether it could be generalized to general potentials, and an earlier attempt was rather awkward. This is what we succeeded in doing, with Manon Michel and Sebastian C. Kapfer, in a 2014 paper in Journal of Chemical Physics. In the paper, we introduce a factorized Metropolis filter and the concept of infinitesimal Monte Carlo moves to design a rejection-free Markov-chain Monte Carlo algorithm for interacting particle systems that breaks detailed balance yet satisfies global balance. This event-driven algorithm generalizes the recent hard-sphere event-chain Monte Carlo method without introducing any discretizations in time or in space. We demonstrate considerable speed-ups of this method with respect to the classic local Metropolis algorithm. The new algorithm generates a continuum of samples of the stationary probability density. This allows us to derive an exact formula for the pressure that is obtained as a byproduct of the simulation without any additional computations. The generalized event-chain algorithm is really simple to implement, and it showed all its usefulness, for example in recent simulations with Sebastian C. Kapfer.

Sampling from a polytope and hard-disk Monte Carlo

The hard-disk problem, the statics and the dynamics of equal two-dimensional hard spheres in a periodic box, has had a profound influence on statistical and computational physics. Markov-chain Monte Carlo and molecular dynamics were first discussed for this model. In a recent preprint with Sebastian Kapfer, we were able to reformulate hard-disk Monte Carlo algorithms in terms of another classic problem, namely the sampling from a polytope. Local Markov-chain Monte Carlo, as proposed by Metropolis et al. in 1953, appears as a sequence of random walks in high-dimensional polytopes, while the moves of the more powerful event-chain algorithm correspond to molecular dynamics evolution. In the paper, we determine the convergence properties of Monte Carlo methods in a special invariant polytope associated with hard-disk configurations, and the implications for convergence of hard-disk sampling. Finally, we discuss parallelization strategies for event-chain Monte Carlo and present results for a multicore implementation.

Hard-disk equation of state: First-order liquid-hexatic transition in two dimensions with three simulation methods

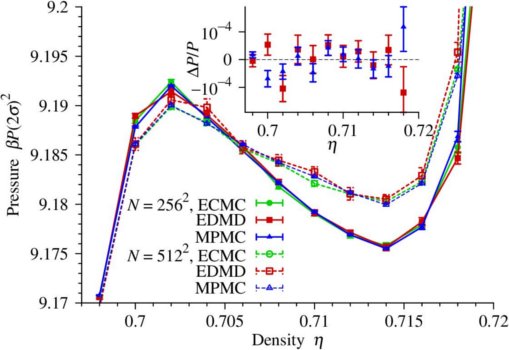
Spring and summer of 2012 was partly spent on a project with colleagues Michael Engel, Joshua Anderson, and Sharon Glotzer from the University of Michigan, Masaharu Isobe from the Nagoya Institute of Technology, and Etienne Bernard from MIT. We were interested in checking our earlier results on the melting transition of hard disks in two dimensions which predicted the existence of a first-order liquid-hexatic phase transition - a big surprise after hundreds of other papers had fought over two other scenarios for melting in two dimensions. Our confirmation preprint finally came out in November 2012, and it was published in April 2013 in Physical Review E, which in 2018 recognized it as its milestone paper for that year. Using three completely independent algorithms (massively parallel local Monte Carlo, molecular dynamics, event-chain Monte Carlo), we confirmed our earlier data (see figure to the left). We are all happy about this independent verification, and Etienne Bernard and I are quite relieved, as so much can go wrong with numerical simulations, especially if they take an eternity, almost, to run.

The figure to the left shows the equation of state for hard disks (the equilibrium pressure as a function of the density (or the volume), with the characteristic loop which indicates the presence of two phases - a minority phase that forms a bubble inside the majority phase. The three curves stand for the simulation methods: different algorithms, different computers, even continents produce the same equation of state, the one that noone else has produced before! The inset gives the difference between the old data (from last year) and the new ones. Let me note that, if the simulation is nontrivial, the calculation of the pressure is quite tricky also, especially in Monte Carlo calculations, as an extrapolation of the pair-correlation function is involved. Those of us in the team who computed the pressure from Monte Carlo were much relieved to see the nice agreement with the molecular dynamics pressure, obtained with Masaharu Isobe's code, which is computed simply by counting the number of collisions taking place over a months-long simulation. For more details, take a look at the paper.

Event-driven Monte Carlo algorithm for general potentials

In recent works, as for example on the melting transition in two dimensions, the event-chain algorithm has proven quite helpful. This hard-sphere Monte Carlo method runs a lot faster than earlier methods although the speed-uo remains constant for large system sizes. Nevertheless, gaining a factor of about 100 is not so bad for run-times (with the new algorithm) on the order of a few months... we got our results before it was time to retire.

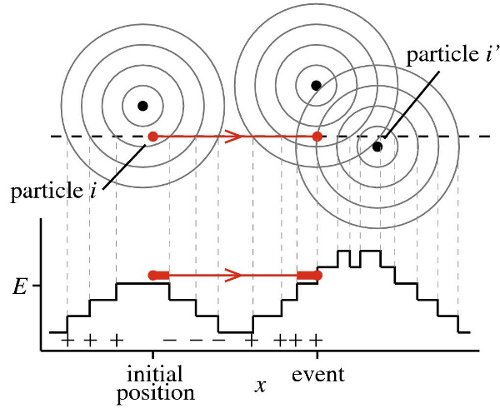
Recently, in 2012, Etienne Bernard (now at MIT) and I were able to extend the event-chain algorithm to continuous potentials, and we are now quite excited: The algorithm allows to break detailed balance, it is (hopefully) much faster than local Monte Carlo algorithms, and it is extremely easy to program, to parallelize (hopefully), to modify and, why not, to improve. Technically, we work with stepped potentials (see the figure, similar approaches exist for molecular dynamics), but there is no problem going to finer and finer discretizations: the algorithm doesn't even slow down as we crank up the number of steps. This is explained in a section of the wiki page dedicated to our recent paper. But lots of things need to be done to understand this new approach, to check out possible applications, etc, and we are right now extremely busy.

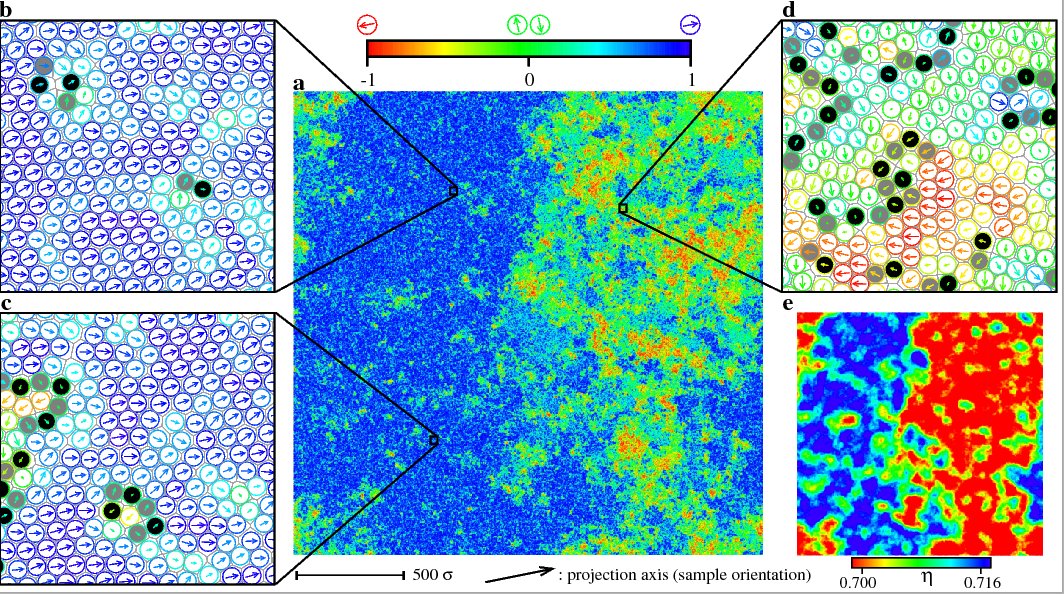
Two-dimensional melting: First-order liquid-hexatic transition

Here, I show the key figure of a recent paper, published in Physical Review Letters in 2011, with Etienne Bernard, on the melting transition in hard disks. The main picture shows the orientations of a configuration with 1024x1024 disks, and two different regions are clearly visible: To the left, disks have more or less the same orientation, whereas to the right, the orientations vary (and the local densities are lower). This clearly indicates the presence of a first-order transition (for details see the paper). In our paper, we show not only that the transition is of first order, but also that it is between the liquid and a hexatic phase. Our melting scenario differs from what hundreds of earlier papers seemed to indicate, namely that the two-dimensional melting transition either followed the famous KTHNY scenario or was a direct transition from the liquid to the solid state, as in three dimensions. The fight for truth between these two groups raged for several decades. Using much better simulation methods, we could show that both were off, and the scenario adopted by nature is not what was imagined for so long.

To produce the picture, we used the event-chain algorithm, a Monte Carlo method that we developed a few years ago, with David Wilson. This algorithm is really the first one to outperform, by about two orders of magnitude in speed, the classic Metropolis method from 1953. For a long time, I have been interested in the hard-disk melting problem, but an earlier attempt to speed up the extremely slow converge of numerical methods for this problem, the cluster algorithm that I developed with C. Dress, had failed.
Return to the "Current Research" section