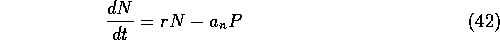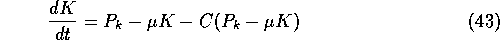Next: Algebraic analysis
Up: Influence of capital
Previous: Numerical results
In the previous sections, the consumption
was taken to be proportional to
the profits, ie 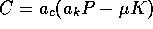 .
This assumption was
not meant to describe consumption patterns when profits are low:
consumption would become negative with negative profits.
In fact the consumption by itself did not directly
play a role in the mathematical model, since the differential
equation for the capital contained only the replenishment term
which is simply proportional to the profits.
A term like this corresponds to the availability
of funds, which have been generated by other economic activities,
to maintain the fishermen and the fisheries when their profits are small.
On the other hand, one can be interested in the
extreme case when no savings and no external income are
available, and when a minimal level of consumption is
necessary for the fishermen. Such would be the case,
for instance, in a primitive society whose economy
depends on a single resource.
In order to study this case we assume
that the consumption, C, is proportional to the
profits when they are high, but that some minimum
positive consumption,
.
This assumption was
not meant to describe consumption patterns when profits are low:
consumption would become negative with negative profits.
In fact the consumption by itself did not directly
play a role in the mathematical model, since the differential
equation for the capital contained only the replenishment term
which is simply proportional to the profits.
A term like this corresponds to the availability
of funds, which have been generated by other economic activities,
to maintain the fishermen and the fisheries when their profits are small.
On the other hand, one can be interested in the
extreme case when no savings and no external income are
available, and when a minimal level of consumption is
necessary for the fishermen. Such would be the case,
for instance, in a primitive society whose economy
depends on a single resource.
In order to study this case we assume
that the consumption, C, is proportional to the
profits when they are high, but that some minimum
positive consumption, 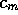 ,
is maintained even when profits are
small or negative.
A simple way of expressing this is
to say that the consumption is a function of
,
is maintained even when profits are
small or negative.
A simple way of expressing this is
to say that the consumption is a function of 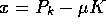 , with
, with
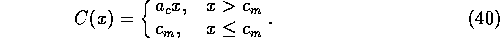
However, this assumption gives a consumption function which has a
discontinuous derivative: besides making the mathematical analysis
at 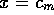 difficult, this sharp transition is not realistic.
A smoothed version of this function is
difficult, this sharp transition is not realistic.
A smoothed version of this function is
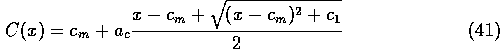
where 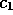 is a positive constant which
determines the sharpness of the corner near
is a positive constant which
determines the sharpness of the corner near 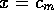 .
We assume, as before, that
.
We assume, as before, that 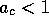 , so that the fraction consumed at high profits
is less than 1. This consumption function, shown in figure 10, has the desired properties
that
, so that the fraction consumed at high profits
is less than 1. This consumption function, shown in figure 10, has the desired properties
that 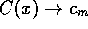 as
as 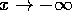 and
and 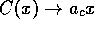 as
as
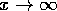 . Both C and
. Both C and 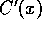 are monotonically increasing in x.
are monotonically increasing in x.
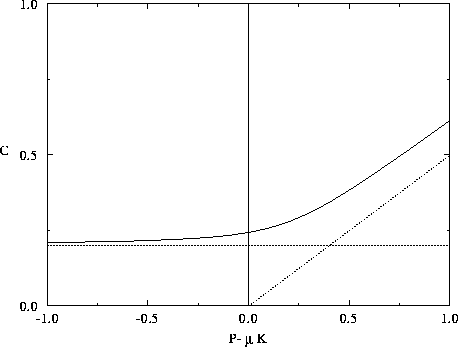
Figure 10: Consumption function used in section 5.
The horizontal axis represents the profit 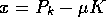 .
A minimum consumption,
.
A minimum consumption, 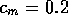 , is maintained, even in the absence of
profit. When profits are are high, consumption increases in proportion to x, with a constant of proportionality
, is maintained, even in the absence of
profit. When profits are are high, consumption increases in proportion to x, with a constant of proportionality 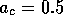 as in section 2.
Here the sharpness of the corner is defined by
as in section 2.
Here the sharpness of the corner is defined by
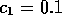 . For comparison the two asymptotes,
. For comparison the two asymptotes,
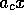 and
and 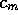 are also shown in dotted lines.
are also shown in dotted lines.
The minimum consumption model
is based on the set of equations
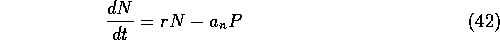
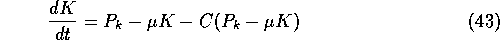
This system is identical to that of section 2, except for the consumption
function term in the capital equation.



Next: Algebraic analysis
Up: Influence of capital
Previous: Numerical results
weisbuch
Fri Feb 7 13:18:37 GMT+0100 1997
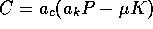 .
This assumption was
not meant to describe consumption patterns when profits are low:
consumption would become negative with negative profits.
In fact the consumption by itself did not directly
play a role in the mathematical model, since the differential
equation for the capital contained only the replenishment term
which is simply proportional to the profits.
A term like this corresponds to the availability
of funds, which have been generated by other economic activities,
to maintain the fishermen and the fisheries when their profits are small.
On the other hand, one can be interested in the
extreme case when no savings and no external income are
available, and when a minimal level of consumption is
necessary for the fishermen. Such would be the case,
for instance, in a primitive society whose economy
depends on a single resource.
In order to study this case we assume
that the consumption, C, is proportional to the
profits when they are high, but that some minimum
positive consumption,
.
This assumption was
not meant to describe consumption patterns when profits are low:
consumption would become negative with negative profits.
In fact the consumption by itself did not directly
play a role in the mathematical model, since the differential
equation for the capital contained only the replenishment term
which is simply proportional to the profits.
A term like this corresponds to the availability
of funds, which have been generated by other economic activities,
to maintain the fishermen and the fisheries when their profits are small.
On the other hand, one can be interested in the
extreme case when no savings and no external income are
available, and when a minimal level of consumption is
necessary for the fishermen. Such would be the case,
for instance, in a primitive society whose economy
depends on a single resource.
In order to study this case we assume
that the consumption, C, is proportional to the
profits when they are high, but that some minimum
positive consumption, 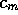 ,
is maintained even when profits are
small or negative.
A simple way of expressing this is
to say that the consumption is a function of
,
is maintained even when profits are
small or negative.
A simple way of expressing this is
to say that the consumption is a function of 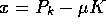 , with
, with
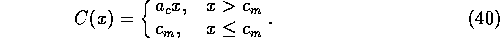
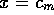 difficult, this sharp transition is not realistic.
A smoothed version of this function is
difficult, this sharp transition is not realistic.
A smoothed version of this function is
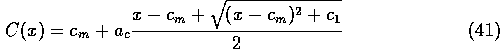
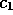 is a positive constant which
determines the sharpness of the corner near
is a positive constant which
determines the sharpness of the corner near 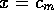 .
We assume, as before, that
.
We assume, as before, that 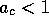 , so that the fraction consumed at high profits
is less than 1. This consumption function, shown in figure
, so that the fraction consumed at high profits
is less than 1. This consumption function, shown in figure 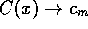 as
as 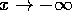 and
and 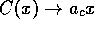 as
as
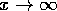 . Both C and
. Both C and 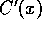 are monotonically increasing in x.
are monotonically increasing in x.

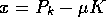 .
A minimum consumption,
.
A minimum consumption, 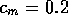 , is maintained, even in the absence of
profit. When profits are are high, consumption increases in proportion to x, with a constant of proportionality
, is maintained, even in the absence of
profit. When profits are are high, consumption increases in proportion to x, with a constant of proportionality 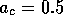 as in section 2.
Here the sharpness of the corner is defined by
as in section 2.
Here the sharpness of the corner is defined by
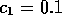 . For comparison the two asymptotes,
. For comparison the two asymptotes,
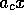 and
and 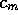 are also shown in dotted lines.
are also shown in dotted lines.