 , June 2023), journal articles (recently appeared here).
, June 2023), journal articles (recently appeared here).
 , June 2023), journal articles (recently appeared here).
, June 2023), journal articles (recently appeared here).
Also available:
 , June 2023), proceedings, conference papers and review articles (
, June 2023), proceedings, conference papers and review articles ( , Nov. 2023)
, Nov. 2023)
 , Jan 2023)
, Jan 2023)
Most publications can be downloaded from this site. Otherwise, just ask me (jean-pierre.nadal "at " phys.ens.fr).
Last modified on November 29, 2023
 Nirbhay Patil, Jean-Pierre Nadal, Jean-Philippe Bouchaud
Nirbhay Patil, Jean-Pierre Nadal, Jean-Philippe Bouchaud
Classification is one of the major tasks that deep learning is successfully tackling. Categorization is also a fundamental cognitive ability. A well-known perceptual consequence of categorization in humans and other animals, called categorical perception, is characterized by a within-category compression and a between-category separation: two items, close in input space, are perceived closer if they belong to the same category than if they belong to different categories. Elaborating on experimental and theoretical results in cognitive science, here we study categorical effects in artificial neural networks. Our formal and numerical analysis provides insights into the geometry of the neural representation in deep layers, with expansion of space near category boundaries and contraction far from category boundaries. We investigate categorical representation by using two complementary approaches: one mimics experiments in psychophysics and cognitive neuroscience by means of morphed continua between stimuli of different categories, while the other introduces a categoricality index that quantifies the separability of the classes at the population level (a given layer in the neural network). We show on both shallow and deep neural networks that category learning automatically induces categorical perception. We further show that the deeper a layer, the stronger the categorical effects. An important outcome of our analysis is to provide a coherent and unifying view of the efficacy of different heuristic practices of the dropout regularization technique. Our views, which find echoes in the neuroscience literature, insist on the differential role of noise as a function of the level of representation and in the course of learning: noise injected in the hidden layers gets structured according to the organization of the categories, more variability being allowed within a category than across classes.
(Copyright © the MIT Press, 2022).
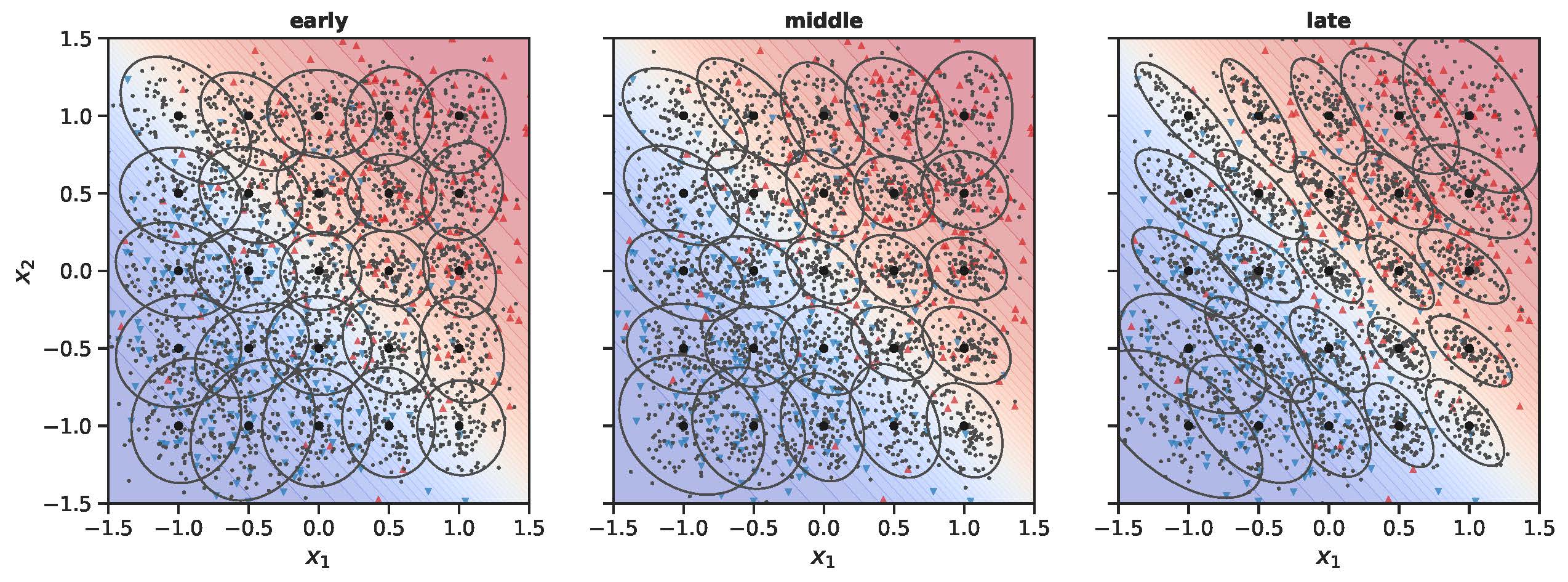
Illustration of the extension of neural space near the class boundary and contraction away from it or along non relevant directions (Fig. 2 from the above paper). Two dimensional example with two Gaussian categories. Evolution of the neural geometry over the course of learning. In the 2d input space, the background color indicates the true posterior probabilities from blue (category 1) to red (category 2) through white (region between categories). Each ellipse represents the set of inputs having a neural representation very close to the one of the input at the center of the ellipse. From left to right: early, intermediate and late learning stages. See paper for details.
Related work ( , Dec. 2023): Conference paper, talk at InfoCog@neurIPS2023, see here.
, Dec. 2023): Conference paper, talk at InfoCog@neurIPS2023, see here.
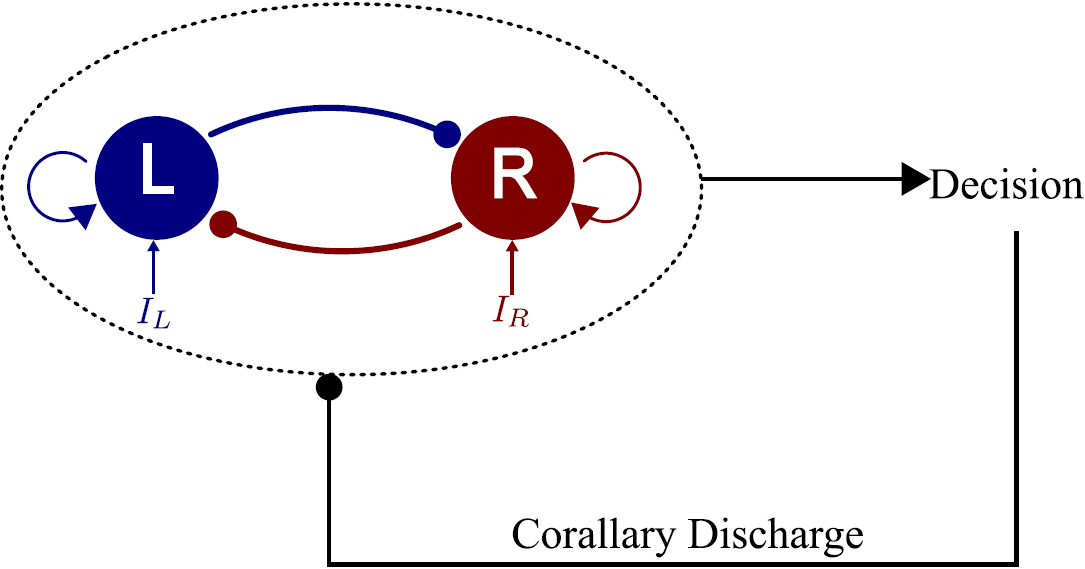
In experiments on perceptual decision-making, individuals learn a categorization task through trial-and-error protocols. We explore the capacity of a decision-making attractor network to learn a categorization task through reward-based, Hebbian type, modifications of the weights incoming from the stimulus encoding layer. For the latter, we assume a standard layer of a large number of stimulus specific neurons. Within the general framework of Hebbian learning, authors have hypothesized that the learning rate is modulated by the reward at each trial. Surprisingly, we find that, when the coding layer has been optimized in view of the categorization task, such reward-modulated Hebbian learning (RMHL) fails to extract efficiently the category membership. In a previous work we showed that the attractor neural networks nonlinear dynamics accounts for behavioral confidence in sequences of decision trials. Taking advantage of these findings, we propose that learning is controlled by confidence, as computed from the neural activity of the decision-making attractor network. Here we show that this confidence-controlled, reward-based, Hebbian learning efficiently extracts categorical information from the optimized coding layer. The proposed learning rule is local, and, in contrast to RMHL, does not require to store the average rewards obtained on previous trials. In addition, we find that the confidence-controlled learning rule achieves near optimal performance.
(Copyright © the MIT Press, 2022).
Recently single neurons measurements during perceptual decision tasks in monkeys have coupled the neural mechanisms of decision making and the establishment of a degree of confidence. These neural mechanisms have been investigated in the context of a spiking attractor network model. It has been shown that confidence about a decision under uncertainty can be computed using a simple neural signal in individual trials. However, it remains unclear if a neural attractor network can reproduce the behavioral effects of confidence in humans. To answer this question, we designed an experiment in which participants were asked to perform an orientation discrimination task, followed by a confidence judgment. Here we show for the first time that an attractor neural network model, calibrated separately on each participant, accounts for full sequences of decision-making. Remarkably, the model is able to reproduce quantitatively the relations between accuracy, response times and confidence, as well as various sequential effects such as the influence of confidence on the subsequent trial. Our results suggest that a metacognitive process such as confidence in perceptual decision can be based on the intrinsic dynamics of a nonlinear attractor neural network.
Article published under a Creative Commons Attribution 4.0 International License.
Perceptual decision-making is the subject of many experimental and theoretical studies.
Most modeling analyses are based on statistical processes of accumulation of evidence. In contrast, very few works confront attractor network models' predictions with empirical data from continuous sequences of trials.
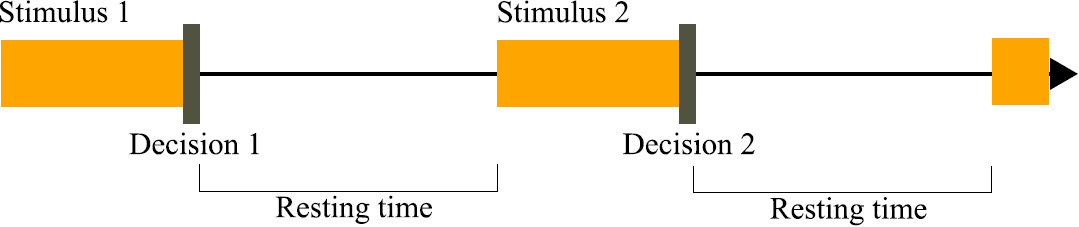
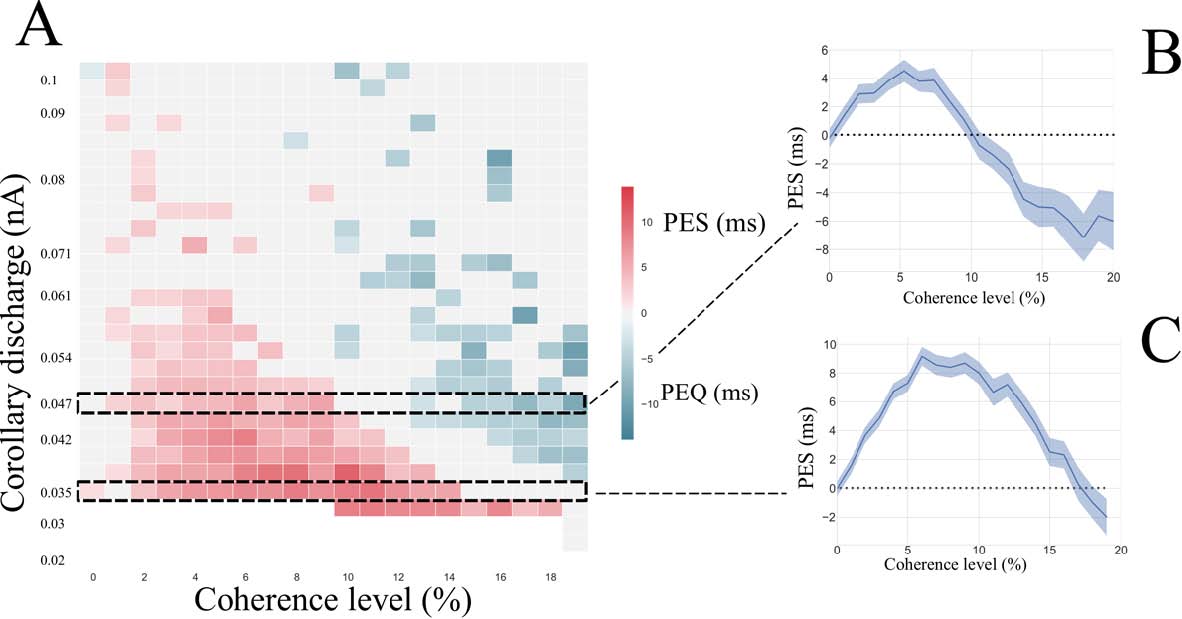
Recently however, numerical simulations of a biophysical competitive attractor network model have shown that such network can describe sequences of decision trials and reproduce repetition biases observed in perceptual decision experiments. Here we get more insights into such effects by considering an extension of the reduced attractor network model of Wong and Wang (2006), taking into account an inhibitory current delivered to the network once a decision has been made. We make explicit the conditions on this inhibitory input for which the network can perform a succession of trials, without being either trapped in the first reached attractor, or losing all memory of the past dynamics.
We study in details how, during a sequence of decision trials, reaction times and performance depend on the nonlinear dynamics of the network, and we confront the model behavior with empirical findings on sequential effects.
Here we show that, quite remarkably, the network exhibits, qualitatively and with the correct orders of magnitude, post-error slowing and post-error improvement in accuracy, two subtle effects reported in behavioral experiments
in the absence of any feedback about the correctness of the decision.
Our work thus provides evidence that such effects result from intrinsic properties of the nonlinear neural dynamics.
Work published by SFN (The Society for Neuroscience) under the license Creative Commons Attribution 4.0 International License (CC-BY).
The cerebellum aids the learning of fast, coordinated movements. According to current consensus, erroneously active parallel fibre synapses are depressed by complex spikes signalling movement errors. However, this theory cannot solve the credit assignment problem of processing a global movement evaluation into multiple cell-specific error signals. We identify a possible implementation of an algorithm solving this problem, whereby spontaneous complex spikes perturb ongoing movements, create eligibility traces and signal error changes guiding plasticity. Error changes are extracted by adaptively cancelling the average error. This framework, stochastic gradient descent with estimated global errors (SGDEGE), predicts synaptic plasticity rules that apparently contradict the current consensus but were supported by plasticity experiments in slices from mice under conditions designed to be physiological, highlighting the sensitivity of plasticity studies to experimental conditions. We analyse the algorithm’s convergence and capacity. Finally, we suggest SGDEGE may also operate in the basal ganglia.
© 2023 eLife Sciences Publications Ltd. Subject to a Creative Commons Attribution license (CC BY 4.0).
As a large-scale instance of dramatic collective behavior, the 2005 French riots started in a poor suburb of Paris, then spread in all of France, lasting about three weeks. Remarkably, although there were no displacements of rioters, the riot activity did traveled. Daily national police data to which we had access have allowed us to take advantage of this natural experiment to explore the dynamics of riot propagation. Here we show that an epidemic-like model, with less than 10 free parameters and a single sociological variable characterizing neighborhood deprivation, accounts quantitatively for the full spatio-temporal dynamics of the riots. This is the first time that such data-driven modeling involving contagion both within and between cities (through geographic proximity or media) at the scale of a country is performed. Moreover, we give a precise mathematical characterization to the expression ``wave of riots'', and provide a visualization of the propagation around Paris, exhibiting the wave in a way not described before. The remarkable agreement between model and data demonstrates that geographic proximity played a major role in the riot propagation, even though information was readily available everywhere through media. Finally, we argue that our approach gives a general framework for the modeling of spontaneous collective uprisings.
Videos (click on the images): wave propagation in Paris area. Color: riot intensity. Size of the circles: for each municipality, in proportion of the size of the deprived population. Left: video based on the data after smoothing. Right: video based on the calibrated epidemiological model. See the paper for details.
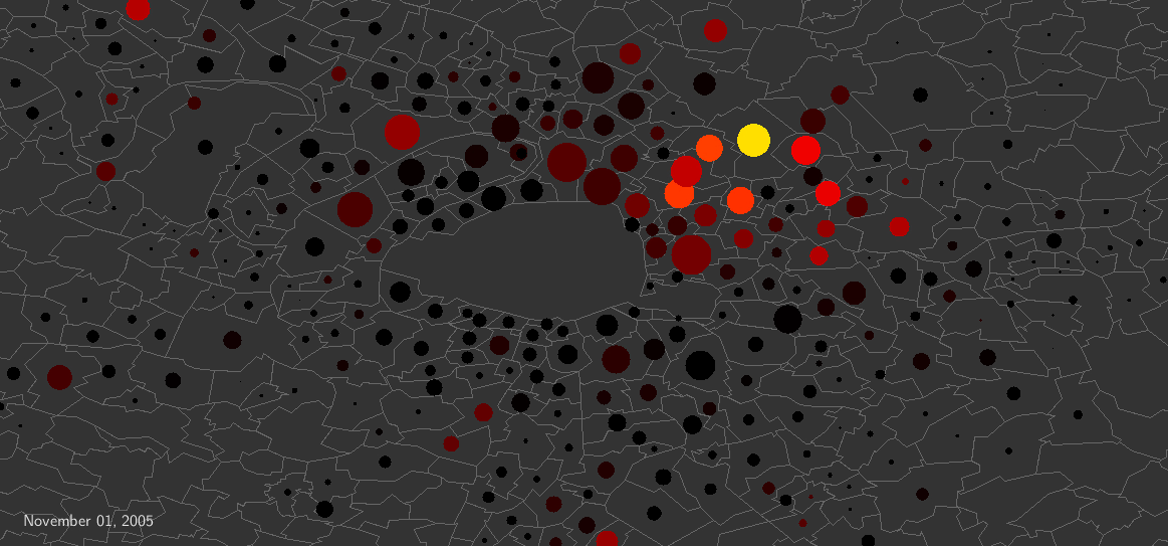

Article, figures, videos published under a Creative Commons Attribution 4.0 International License.
Echos:
Altmetric, "Attention score": in the top 5% of all research outputs ever tracked by Altmetric (Aug. 7, 2018)
MIT Technology Review, Top Stories, Feb 3, 2017 - also in the Spanish edition
France Inter : « Les émeutes contagieuses », interview pour la séquence 'La Une de la science' de l’émission 'La tête au carré', 25 janvier 2018
Le Monde, « Les émeutes de 2005 vues comme une épidémie de grippe », Jan. 22, 2018
It is generally believed that when a linguistic item acquires a new
meaning, its overall frequency of use rises with time with an S-shaped
growth curve. Yet, this claim has only been supported by a limited
number of case studies. In this paper, we provide the first corpus-based
large-scale confirmation of the S-curve in language change. Moreover,
we uncover another generic pattern, a latency phase preceding the
S-growth, during which the frequency remains close to constant. We
propose a usage-based model which predicts both phases, the latency and
the S-growth. The driving mechanism is a random walk in the space of
frequency of use. The underlying deterministic dynamics highlights the
role of a control parameter which tunes the system at the vicinity of a
saddle-node bifurcation. In the neighbourhood of the critical point, the
latency phase corresponds to the diffusion time over the critical
region, and the S-growth to the fast convergence that follows. The
durations of the two phases are computed as specific first-passage
times, leading to distributions that fit well the ones extracted from
our dataset. We argue that our results are not specific to the studied
corpus, but apply to semantic change in general.
© 2017 The Authors. Published by the Royal Society under the terms of the Creative Commons Attribution License (CC BY 4.0) which permits unrestricted use, provided the original author and source are credited.
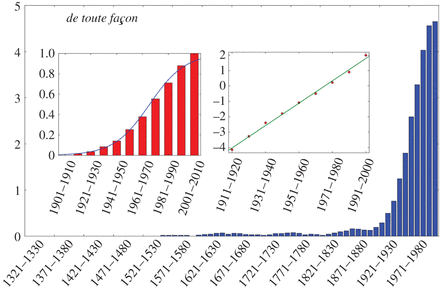
See also:
Same authors, "Modeling Language Change: The Pitfall of Grammaticalization",
Chapter in "Language in Complexity: The Emerging Meaning", Springer 2016
Same authors, "Représentation du langage et modèles d'évolution linguistique : la grammaticalisation comme
perspective", TAL, 2016 (below)
Quentin Feltgen, PhD Thesis, Statistical physics of language evolution : the grammaticalization phenomenon, PSL University, 2017.
For this Thesis, Quentin received the (French) 2018 1st price for thesis in the field of complex systems, see here.
Though numerous numerical studies have investigated language change,
grammaticalization and diachronic phenomena of language renewal have
been left aside, or so it seems. We argue that previous models,
dedicated to other purposes, make representational choices that cannot
easily account for this type of phenomenon. In this paper we propose a
new framework, aiming to depict linguistic renewal through numerical
simulations. We illustrate it with a specific implementation which
brings to light the phenomenon of semantic bleaching.
(article in French) (Copyright © ATALA 2016)
Related paper, in English, same authors: "Modeling Language Change: The Pitfall of Grammaticalization", Chapter in "Language in Complexity: The Emerging Meaning", Springer 2016, pp. 49-72. See also above.
Related works:
L. Gauvin et al, "Schelling segregation in an open city: a kinetically constrained Blume-Emery-Griffiths spin-1 system", 2010 - see below.
L. Gauvin et al, "Phase diagram of a Schelling segregation model", 2009 - see below.
L. Gauvin, PhD Thesis, Modélisation de systèmes socio-économiques à l'aide des outils de physique statistique, UPMC, 2010.
Entanglement between Demand and Supply in Markets with Bandwagon Goods
Journal of Statistical Physics: Volume 151, Issue 3 (2013), Page 494-522
(this article is part of the special issue Statistical Mechanics and Social Sciences, II)
preprint arXiv:1209.1321
(This work: copyright © Springer 2012)
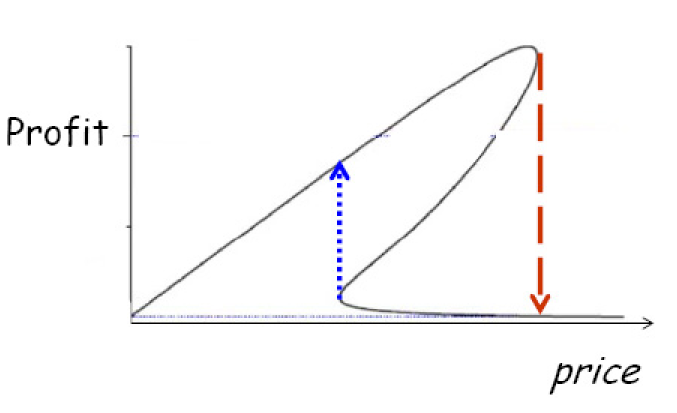
In case of bandwagon goods, the demand can show multiple Nash equilibria. This leads to a systemic risk for the seller: the price maximizing the profit is very close to the one at which the large demand disapears.
Related work:
Same authors, "Discrete Choices under Social Influence: Generic Properties", M3AS 2009, below.
Between order and disorder: a 'weak law' on recent electoral behavior among urban voters?
PLoS ONE 7(7): e39916 (published: July 25, 2012).
preprint arXiv:1202.6307
A new viewpoint on electoral involvement is proposed from the study of
the statistics of the proportions of abstentionists, blank and null, and
votes according to list of choices, in a large number of national
elections in different countries. Considering 11 countries without
compulsory voting (Austria, Canada, Czech Republic, France, Germany,
Italy, Mexico, Poland, Romania, Spain and Switzerland), a stylized fact
emerges for the most populated cities when one computes the entropy
associated to the three ratios, which we call the entropy of civic
involvement of the electorate. The distribution of this entropy (over
all elections and countries) appears to be sharply peaked near a common
value. This almost common value is typically shared since the 1970's by
electorates of the most populated municipalities, and this despite the
wide disparities between voting systems and types of elections.
Performing different statistical analyses, we notably show that this
stylized fact reveals particular correlations between the blank/null
votes and abstentionists ratios.
We suggest that the existence of this hidden regularity, which we
propose to coin as a `weak law on recent electoral behavior among urban
voters', reveals an emerging collective behavioral norm characteristic
of urban citizen voting behavior in modern democracies. Analyzing
exceptions to the rule provide insights into the conditions under which
this normative behavior can be expected to occur.
Published under the Creative Commons Attribution (CC BY) license.
Storage of correlated patterns in standard and bistable Purkinje cell models
PLoS Computational Biology, 8(4): e1002448 (2012)
open access -
The cerebellum has long been considered to undergo supervised learning, with climbing
fibers acting as a 'teaching' or 'error' signal. Purkinje cells (PCs), the sole output of the
cerebellar cortex, have been considered as analogs of perceptrons storing input/output
associations. In support of this hypothesis, a recent study found that the distribution
of synaptic weights of a perceptron at maximal capacity is in striking agreement with
experimental data in adult rats. However, the calculation was performed using random
uncorrelated inputs and outputs. This is a clearly unrealistic assumption since sensory in-
puts and motor outputs carry a substantial degree of temporal correlations. In this paper,
we consider a binary output neuron with a large number of inputs, which is required to
store associations between temporally correlated sequences of binary inputs and outputs,
modelled as Markov chains. Storage capacity is found to increase with both input and
output correlations, and diverges in the limit where both go to unity. We also investigate
the capacity of a bistable output unit, since PCs have been shown to be bistable in some
experimental conditions. Bistability is shown to enhance storage capacity whenever the
output correlation is stronger than the input correlation. Distribution of synaptic weights
at maximal capacity is shown to be independent on correlations, and is also unaffected
by the presence of bistability.
Published under the Creative Commons Attribution (CC BY) license.

Related works:
Same authors, "Neural Coding of Categories: Information Efficiency and Optimal Population Codes", J. of Comput. Neuroscience 2008, here.
Same authors, "From Exemplar Theory to Population Coding and Back - An Ideal Observer Approach" (preprint.pdf), proceedings of the workshop "Exemplar-Based Models of Language Acquisition and Use", Dublin, 2007.
Laurent Bonnasse-Gahot, PhD Thesis, Modélisation du codage neuronal de catégories et étude des conséquences perceptives, EHESS, 2009.
This paper considers a variant of the Schelling's segregagtion model. Here the agents can enter or leave the city - a parameter quantifying the attractiveness of the city plays the role of a chemical potential for the number of agents in the city. The considered dynamics is equivalent to the zero-temperature dynamics of the Blume-Emery-Griffiths spin-1 model, with kinetic constraints.
Related works:
Same authors, "Phase diagram of a Schelling segregation model", 2009 - see below.
L. Gauvin, A. Vignes and J.-P. Nadal, "Modeling urban housing market dynamics: can the socio-spatial segregation preserve some social diversity?", JEDC 2013 - see above.
L. Gauvin, PhD Thesis, Modélisation de systèmes socio-économiques à l'aide des outils de physique statistique, UPMC, 2010.
A single social phenomenon (such as crime, unemployment or birth rate)
can be observed through temporal series corresponding to units at
different levels (cities, regions, countries...). Units at a given local
level may follow a collective trend imposed by external conditions, but
also may display fluctuations of purely local origin. The local
behavior is usually computed as the difference between the local data
and a global average (e.g. a national average), a view point which can
be very misleading. In this article, we propose a method for separating
the local dynamics from the global trend in a collection of correlated
time series. We take an independent component analysis approach in which
we do not assume a small average local contribution in contrast with
previously proposed methods. We first test our method on financial time
series for which various data analysis tools have already been used. For
the S&P500 stocks, our method is able to identify two classes of
stocks with marked different behaviors: the `followers' (stocks driven
by the collective trend), and the `leaders' (stocks for which local
fluctuations dominate). Furthermore, as a byproduct contributing to its
validation, the method also allows to classify stocks in several groups
consistent with industrials sectors. We then consider crime rate series,
a domain where the separation between global and local policies is
still a major subject of debate. We apply our method to the states in
the US and the regions in France. In the case of the US data, we observe
large fluctuations in the transition period of mid-70's during which
crime rates increased significantly, whereas since the 80's, the state
crime rates are governed by external factors, and the importance of
local specificities being decreasing.
Copyright PNAS, see here.
Echo in the nonacademic press: Where local policy matters, 16 April 2010, in Emerging Health Threats Forum (a not-for-profit Community Interest Company, established with support from the UK's Health Protection Agency).
This paper summarizes the effects of social influences in a monopoly
market with heterogeneous agents. The market equilibria are presented in
the limiting case of global influence. Considering static profit
maximization there may exist two different regimes: to sell either to a
large fraction of customers at a low price, or to a small fraction of
them at a higher price. This arises for numerous mono-modal
distributions of idiosyncratic willingness to pay if the social
influence is strong enough. The seller's optimal strategy switches from
one regime to the other at parameter values where the demand has two
different Nash equilibria; but the strategy of posting low prices to
attract large fractions of buyers may fail due to a lack of
coordination.
Intellectual property rules concerning this paper: see here.
Related works:
Same authors, "Entanglement between Demand and Supply in Markets with Bandwagon Goods", J. Stat. Phys. 2013, above
Same authors, "Discrete Choices under Social Influence: Generic Properties", M3AS 2009, below.
This work proposes a numerical study of the original segregation model of Schelling. Making use of statistical physics tools, it establishes the full phase diagram for this model. It also exhibits links with spin-1 models.
Related works:
Same authors, "Schelling segregation in an open city: a kinetically constrained Blume-Emery-Griffiths spin-1 system", 2010 - see above.
L. Gauvin, A. Vignes and J.-P. Nadal, "Modeling urban housing market dynamics: can the socio-spatial segregation preserve some social diversity?", JEDC 2013 - see above.
L. Gauvin, PhD Thesis, Modélisation de systèmes socio-économiques à l'aide des outils de physique statistique, UPMC, 2010.
We consider a model of socially interacting individuals that make a
binary choice in a context of positive additive endogenous
externalities. It encompasses as particular cases several models from the sociology and economics literature. We extend previous results to the case of a general distribution of idiosyncratic preferences, called here Idiosyncratic Willingnesses to Pay (IWP).
Positive additive externalities yield a family of inverse demand curves that include the classical downward sloping ones but also new ones with non constant convexity. When $j$, the ratio of the social influene strength to the standard deviation of the IWP distribution, is small enough, the inverse demand is a classical monotonic (decreasing) function of the adoption rate. Even if the IWP distribution is
mono-modal, there is a critical value of $j$ above which the inverse demand is non monotonic, decreasing for small and high adoption rates, but increasing within some intermediate range. Depending on the price there are thus either one or two equilibria.
Beyond this first result, we exhibit the generic properties of the boundaries limiting the regions where the system presents different types of equilibria (unique or multiple). These properties are shown to depend only qualitative features of the IWP distribution: modality (number of maxima), smoothness and type of support (compact or
infinite). The main results are summarized as phase diagrams in the space of the model parameters, on which the regions of multiple equilibria are precisely delimited.
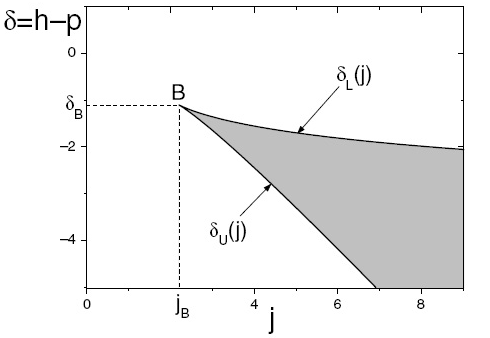
(© World Scientific)
Related works:
Same authors, "Entanglement between Demand and Supply in Markets with Bandwagon Goods", J. Stat. Phys. 2013, above.
J.-P. Nadal et al, "Multiple equilibria in a monopoly market with heterogeneous agents and externalities", Quantitative Finance 2005, below
M. B. Gordon et al, "Seller's dilemma due to social interactions between customers", Physica A 2005, below.
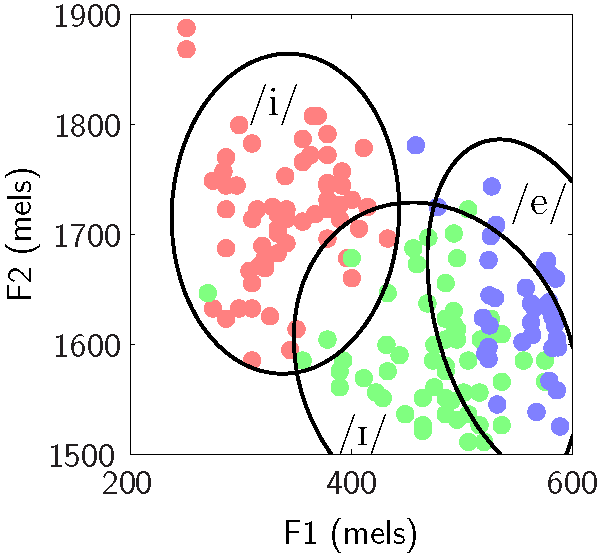

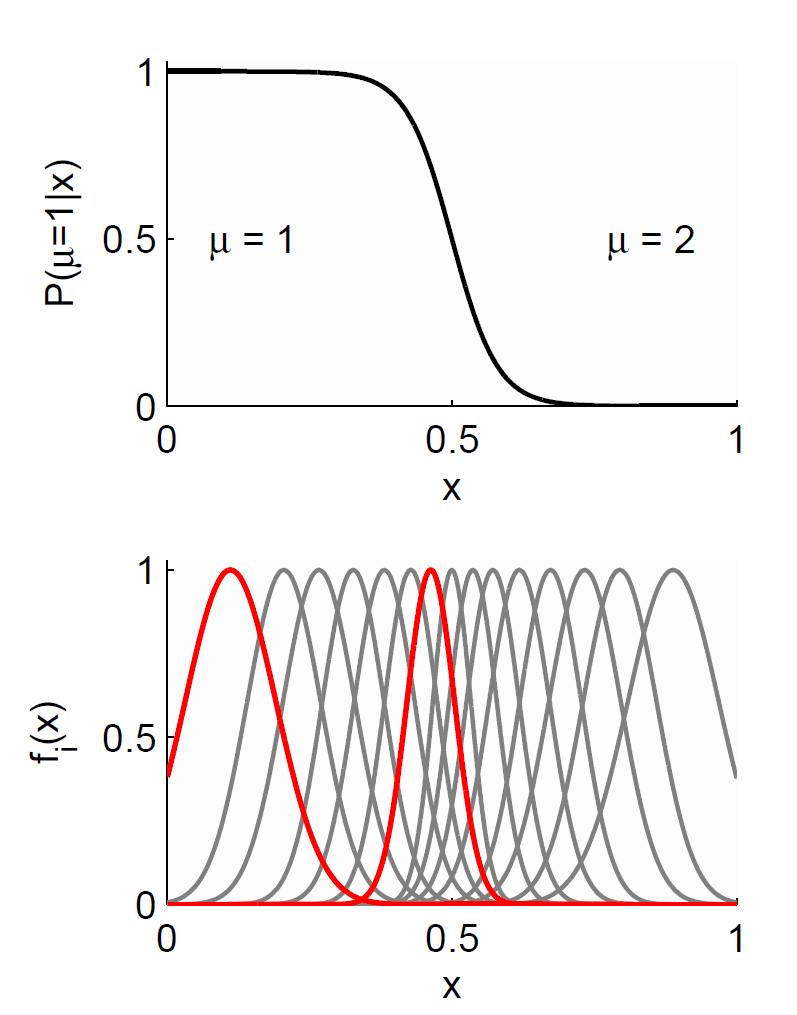
Related works:
Same authors, "Perception of categories: from coding efficiency to reaction times", Brain Research, 2012, here.
Same authors, "From Exemplar Theory to Population Coding and Back - An Ideal Observer Approach" (preprint.pdf), proceedings of the workshop "Exemplar-Based Models of Language Acquisition and Use", Dublin, 2007.
Laurent Bonnasse-Gahot, PhD Thesis, Modélisation du codage neuronal de catégories et étude des conséquences perceptives, EHESS, 2009.
Related works:
M. B. Gordon et al, "Entanglement between Demand and Supply in Markets with Bandwagon Goods", J. Stat. Phys. 2013, here
M. B. Gordon et al, "Discrete Choices under Social Influence: Generic Properties", M3AS 2009, here.
M. B. Gordon et al, "Seller's dilemma due to social interactions between customers", Physica A 2005, here.
Motivation: We consider any collection of microarrays that can be ordered to form a progression,
as a function of time, or severity of disease, or dose of a stimulant, for example. By plotting the
expression level of each gene as a function of time, or severity, or dose, we form an expression
series, or curve, for each gene. While most of these curves will exhibit random fluctuations, some
will contain pattern, and it is these genes which are most likely associated with the independent
variable.
Results: We introduce a method of identifying pattern and hence genes in microarray expression
curves without knowing what kind of pattern to look for. Key to our approach is the sequence
of ups and downs formed by pairs of consecutive data points in each curve. As a benchmark, we
blindly identified yeast cell cycles genes without selecting for periodic or any other anticipated
behaviour.
(Copyright © 2005 Oxford Journals)
Related publications by K. Willbrand (LPS ENS) and Th. Fink (Inst. Curie): see here.
The interpretation of geophysical data, such as images of subsurface
rocks (seismic data, borehole scans), requires one in particular to
perform an elaborate segmentation analysis on strongly textured,
anisotropic, and not necessarily brightness-contrasted images. In this
paper we explore the possibility of deriving new segmentation algorithms
from recent advances in the neural modelling of pre-attentive
segmentation in human vision. More specifically we consider a neural
model proposed by Zhaoping Li. First, we reproduce some specific results
obtained by Zhaoping Li on simple artificial and real images sharing
some textural characteristics with geophysical data. Next, from the
analysis of the model behaviour, we propose an image processing workflow
depending on the textural characteristics and on the type of
segmentation (contour enhancement or texture edge detection) one is
interested in. With this algorithm one gets promising results: from the
computation of a single attribute one extracts the oriented textured
feature boundaries without prior classification.
(Copyright © Institute of Physics and IOP Publishing Limited 2004)
This letter suggests that in biological organisms, the perceived structure
of reality, in particular the notions of body, environment, space, object,
and attribute, could be a consequence of an effort on the part of brains to
account for the dependency between their inputs and their outputs in terms
of a small number of parameters. To validate this idea, a
procedure is demonstrated whereby the brain of an organism with
arbitrary input and output connectivity can deduce the dimensionality
of the rigid group of the space underlying its input-output relationship, that is
the dimension of what the organism will call physical space.
(© 2003 The MIT Press)
Natural images are complex but very structured objects and, in spite of its com-
plexity, the sensory areas in the neocortex in mammals are able to devise learned
strategies to encode them endciently. How is this goal achieved? In this paper, we
will discuss the multiscaling approach, which has been recently used to derive a
redundancy reducing wavelet basis. This kind of representation can be statistically
learned from the data and is optimally adapted for image coding; besides, it presents
some remarkable features found in the visual pathway. We will show that the
introduction of oriented wavelets is necessary to provide a complete description, which
stresses the role of the wavelets as edge detectors.
(Copyright © 2003 Elsevier Science Ltd.)
This article has been selected for the February 15, 2002 issue of the Virtual Journal of Biological Physics Research published by the American Institute of Physics and the American Physical Society.
We address the problem of blind source separation in the case of a
time dependent mixture matrix.
For a slowly and smoothly varying mixture matrix, we propose a systematic expansion
which leads to a practical algebraic solution when
stationary and ergodic properties hold for the sources.
[© 2000 Elsevier Science B. V.]
We investigate the information processing of a linear mixture of independent sources of different magnitudes. In particular we consider the case where a number m of the sources can be considered as “strong” as compared to the other ones, the “weak” sources. We find that it is preferable to perform blind source separation in the space spanned by the strong sources, and that this can be easily done by first projecting the signal onto the m largest principal components. We illustrate the analytical results with numerical simulations.
With the aim of identifying the physical causes of variability of a
given dynamical system, the geophysical community has made an extensive
use of classical component extraction techniques such as principal
component analysis (PCA) or rotational techniques (RT). We introduce a
recently developed algorithm based on information theory: independent
component analysis (ICA). This new technique presents two major
advantages over classical methods. First, it aims at extracting
statistically independent components where classical techniques search
for decorrelated components (i.e., a weaker constraint). Second, the
linear hypothesis for the mixture of components is not required. In this
paper, after having briefly summarized the essentials of classical
techniques, we present the new method in the context of geophysical time
series analysis. We then illustrate the ICA algorithm by applying it to
the study of the variability of the tropical sea surface temperature
(SST), with a particular emphasis on the analysis of the links between
El Niño Southern Oscillation (ENSO) and Atlantic SST variability. The
new algorithm appears to be particularly efficient in describing the
complexity of the phenomena and their various sources of variability in
space and time.
(© 2000 by the American Geophysical Union)
Dans le but d'identifier les causes physiques de la variabilité d'un
système dynamique, la communauté géophysique utilise de façon intensive
les techniques statistiques d'extraction de composantes. Un algorithme
récemment développé, fondé sur la théorie de l'information, est
introduit dans ce travail : l'analyse en composantes indépendantes
(ACI). Cette technique présente deux avantages majeurs sur les
techniques classiques. Premièrement, elle a pour but d'extraire des
composantes statistiquement indépendantes, là où les techniques
classiques cherchent uniquement la décorrélation. Deuxièmement,
l'hypothèse linéaire pour le mélange des composantes n'est pas requise.
Cette nouvelle technique est présenté dans le contexte de l'analyse de
séries temporelles géophysiques. L'algorithme ACI est appliqué à l'étude
de la variabilité de la température de surface de l'océan (TSO)
tropical, avec une attention particulière pour l'analyse des liens entre
le phénomène El Niño/Southern Oscillation (Enso) et la variabilité de
la TSO Atlantique.
(© 1999 - Académie des Sciences/ Éditions Scientifiques et Médicales Elsevier SAS)
Short version presented at NIPS*98:
Didier Herschkowitz and Jean-Pierre Nadal, "Unsupervised clustering:
the mutual information between parameters and observations", in Advances in Neural Information
Processing Systems 11, M. S. Kearns, S. A. Solla, D. A. Cohn, eds., MIT Press 1999, pp. 232-238.
Related works:
D. Herschkowitz and M. Opper, "Retarded Learning: Rigorous Results from Statistical Mechanics",
Phys.Rev.Lett. 86, 2174 (2001).
and above.
We present a formal, although simple, approach to the modeling of a buyer behavior in the type of markets studied in Weisbuch, Kirman and Herreiner, 1995. We compare possible buyer's choice functions, such as linear or logit function. We study the resulting behaviour, showing that they depend on some convexity properties of the choice function. Our results make use of standard Statistical Physics concepts and techniques. In particular we use the "mean field approximation" to derive the long term behaviour of buyers, and we show that the standard "logit" choice function can be justified from a general optimization principle, leading to an exploration-exploitation compromise.
In the context of parameter estimation and model
selection, it is only quite recently that
a direct link between the Fisher information
and information theoretic quantities has been exhibited. We
give an interpretation of this link within the standard
framework of information theory.
We show that in the context of
population coding,
the mutual information between the activity of a large array of neurons and
a stimulus to which the neurons are tuned is naturally related
to the Fisher information.
In the light of this result we consider the optimization
of the tuning curves parameters
in the case of neurons responding to a stimulus
represented by an angular variable.
(Copyright © The MIT Press)
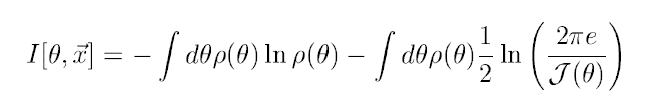
Link between mutual information and Fisher information (limit of large signal to noise ratio, e.g. in the case of population codes).
Here $\theta$ is the stimulus with pdf $\rho$, $x$ the neural activity, and $\cal{J}$ is the Fisher information. See paper for details.
Independent Component Analysis (ICA), and in particular
Blind Source Separation (BSS),
can be obtained from the maximization of mutual information,
as first shown in Nadal and Parga 1994.
The practical interest of this information theoretic
based cost function was then demonstrated in several BSS applications
(see e.g. Bell and Sejnowski 1995, ICA at CNL).
In the present paper the main
result of Nadal and Parga 1994 is extended to the case
of stochastic outputs. More precisely,
we prove that maximization of mutual information between the output
and the input of a feedforward neural network leads to
full redundancy reduction
under the following sufficient
conditions:
(1) the input signal is a (possibly nonlinear) invertible mixture
of independent components; (2) there is no input noise;
(3) the activity of each output neuron is a (possibly) stochastic variable
with a probability distribution depending on the stimulus through
a deterministic function of the inputs; both the probability
distributions and the functions can be different
from neuron to neuron; (4) optimization of the mutual information
is performed over all these deterministic functions.
In the context of both sensory coding and signal processing,
building factorized codes has been shown to be an efficient
strategy. In a wide variety of situations, the signal to be
processed is a linear mixture of statistically independent sources.
Building a factorized code is then equivalent to performing blind
source separation. Thanks to the linear structure of the data, this
can be done, in the language of signal processing, by finding an
appropriate linear filter, or equivalently, in the language of
neural modeling, by using a simple feedforward neural network.
In this article, we discuss several aspects of the source
separation problem. We give simple conditions on the network output
that, if satisfied, guarantee that source separation has been
obtained. Then we study adaptive approaches, in particular those
based on redundancy reduction and maximization of mutual
information. We show how the resulting updating rules are related
to the BCM theory of synaptic plasticity. Eventually we briefly
discuss extensions to the case of nonlinear mixtures. Throughout
this article, we take care to put into perspective our work with
other studies on source separation and redundancy reduction. In
particular we review algebraic solutions, pointing out their
simplicity but also their drawbacks.
(Copyright © The MIT Press)
In this paper we numerically study the performance of the constructive trio-learning algorithm. We show that, from rather limited data sets, one can make extrapolations providing estimates of the error rates on the learning and training sets that would be obtained for large data sizes.
This work has been performed at Laboratoires d'Electronique Philips S.A.S. (LEP), Limeil-Brévannes, France.
See also below, and Florence d'Alché-Buc, PhD Thesis, Modèles neuronaux et algorithmes constructifs pour l'apprentissage de règles de décision, Univ. Paris11 at Orsay, 1993.
We consider a linear, one-layer feedforward neural network performing
a coding task. The goal of the network is to provide a
statistical neural representation that convey
as much information as possible on the input stimuli in noisy conditions.
We determine the family of synaptic couplings that maximizes
the mutual information between input and output distribution.
Optimization is performed under different constraints on the synaptic
efficacies. We analyze the dependence of the solutions on
input and output noises. This work goes beyond previous studies
of the same problem in that:
(i) we perform a detailed stability
analysis in order to find the global maxima of the mutual information;
(ii) we examine the properties of the optimal synaptic configurations
under different constraints;
(iii) we do not assume translational
invariance of the input data, as it is usually
done when input are assumed to be visual stimuli.
Neural trees are constructive algorithms
which build decision trees whose nodes
are binary neurons. We propose a new learning scheme, "trio-learning", which
leads to a significant reduction in the tree complexity. Within the trio strategy, each node
of the tree is optimized by taking into account the knowledge
that it will be followed by two son nodes.
Moreover, trio-learning can be used to
build hybrid trees, with internal nodes and terminal nodes of different nature, for solving
any standard task (e.g. classification, regression, density estimation). Promising
results on a handwritten character classification are presented.
(Copyright © World Scientific Publishing Co.)
This work has been performed at Laboratoires d'Electronique Philips S.A.S. (LEP), Limeil-Brévannes, France.
See also above, and Florence d'Alché-Buc, PhD Thesis, Modèles neuronaux et algorithmes constructifs pour l'apprentissage de règles de décision, Univ. Paris11 at Orsay, 1993.
We investigate the consequences of maximizing information transfer
in a simple neural network (one input layer, one output layer),
focussing on the case of non linear transfer
functions. We assume that both receptive fields
(synaptic efficacies) and transfer functions can be
adapted to the environment.
The main result is that, for bounded and invertible transfer functions,
in the case of a vanishing additive output noise, and no
input noise, maximization of information (Linsker's infomax principle)
leads to a factorial code - hence to the same solution as
required by the redundancy reduction principle of Barlow, or,
in the signal processing language, to Independent Component Analysis (ICA).
We show also that this result is valid for linear,
more generally unbounded,
transfer functions, provided optimization is performed under an
additive constraint, that is which can be written as a
sum of terms, each one being specific to one output neuron.
Finally we study the effect of a non zero input noise. We find that,
at first order in the input noise, assumed to be small as compared
to the - small - output noise,
the above results are still valid, provided the output noise
is uncorrelated from one neuron to the other.
We study the ability of a simple neural network (a perceptron architecture,
no hidden units, binary outputs) to process information in the
context of an unsupervised learning task. The network is asked to
provide the best possible neural representation of a given input
distribution, according to some criterion taken from Information
Theory. We compare various optimization criteria that have been proposed :
maximum information transmission, minimum redundancy and closeness to
factorial code.
We show that for the perceptron one can compute
the maximal information that the code (the output neural representation)
can convey about the input. We show that one can use Statistical
Mechanics techniques, such as the replica techniques, to compute
the typical mutual information between input and output distributions.
More precisely, for a Gaussian input source with a given
correlation matrix, we compute
the typical mutual information when the couplings are chosen randomly. We
determine the correlations between the synaptic couplings
which maximize the gain of information. We analyse the results
in the case of a one dimensional receptive field.
Reconsidering a recently introduced model of sequence-retrieving neural
network, we introduce appropriate analogues of the well-known
stabilities and show how these, together with two coupling parameters
$\lambda$ and $\vartheta$, entirely control the dynamics in the case of
strong dilution. The model is exactly solved and phase diagrams are
drawn for two different choices of the synaptic matrices; they reveal a
rich structure. We then briefly speculate as to the role of these
parameters within a more general framework.
(Copyright © Les Editions de Physique 1993)
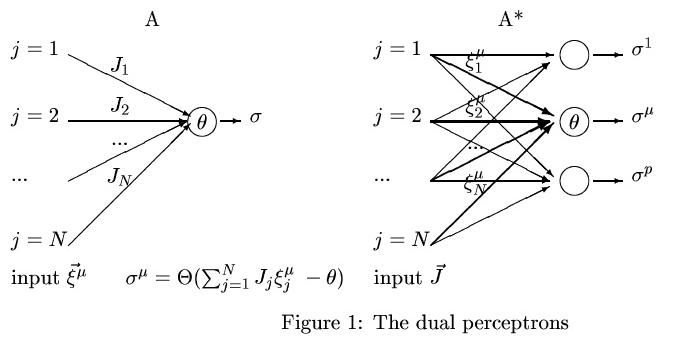
We exhibit a duality between two perceptrons that allows us to
compare the theoretical analysis of supervised and unsupervised
learning tasks - more exactly of parameter estimation
and encoding tasks. The first perceptron has one output and is asked
to learn a classification of p patterns. The second (dual)
perceptron has p outputs and is asked to transmit as much
information as possible on a distribution of inputs. We show in
particular that the maximum information that can be stored in the
couplings for the supervised learning task is equal to the maximum
information that can be transmitted by the dual perceptron.
(Copyright © The MIT Press)
We demonstrate that formal neural networks techniques allow to build the simplest models compatible with a limited but systematic set of experimental data. The experimental system under study is the growth of mouse macrophage like cell lines under the combined influence of two ion channels, the growth factor receptor and adenylate cyclase. We conclude that 3 components out of 4 can be described by linear multithreshold automata. The remaining component behavior being non-monotonous necessitate the introduction of a fifth hidden variable, or of non-linear interactions.
The optimal storage capacity of a perceptron with a finite fraction (1−s) of sign constrained couplings has been computed recently: the basic result is that the capacity is (1+s)/2 times the capacity without sign constraints. In the case of null stability, I show that this simple relation is readily obtained in the geometrical approach à la Cover. Moreover this provides an interpretation valid for any value of the stability.
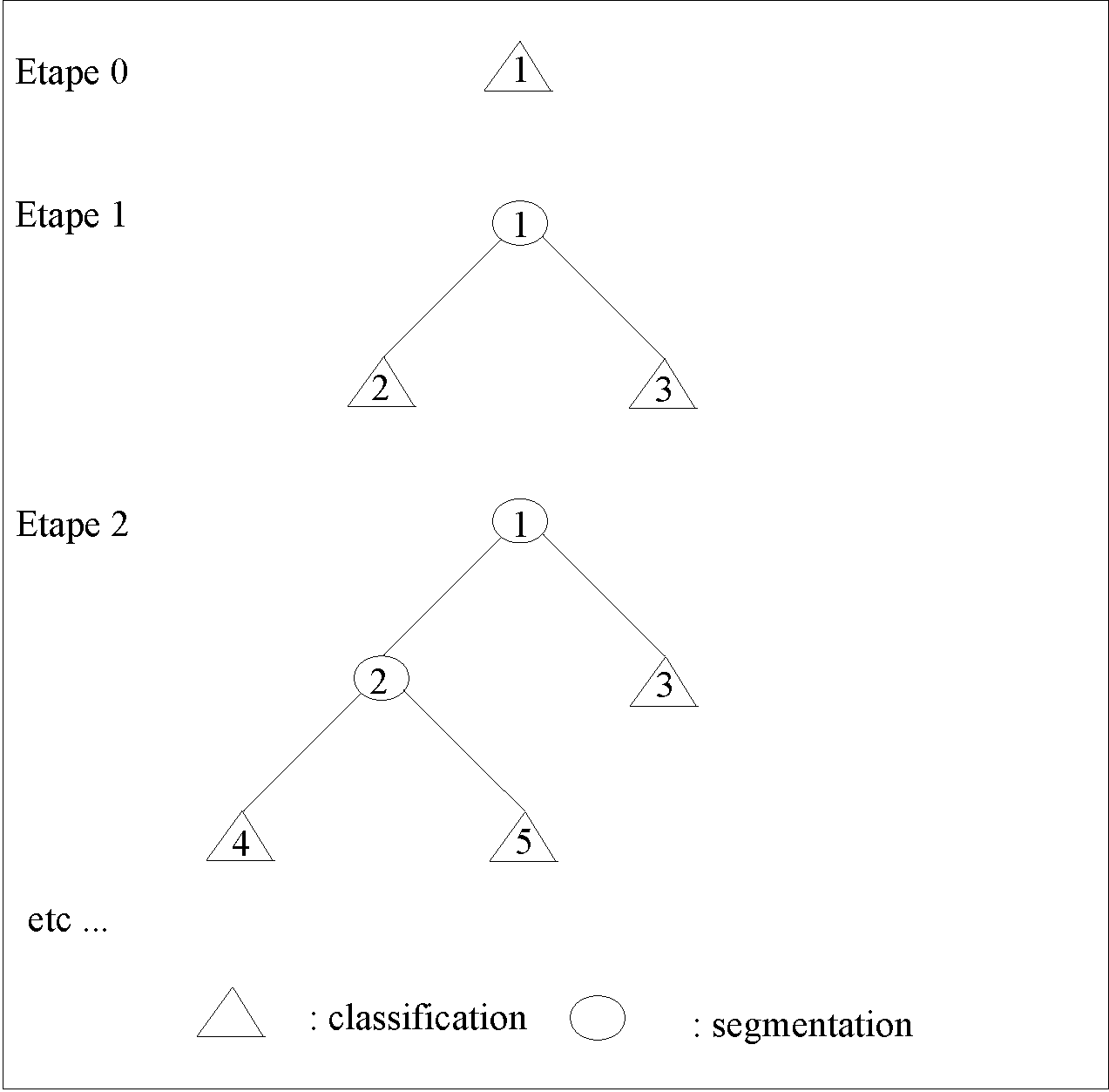
The authors propose a new classifier based on neural network techniques. The ‘network’ consists of a set of perceptrons functionally organized in a binary tree (‘neural tree’). The learning algorithm is inspired from a growth algorithm, the tiling algorithm, recently introduced for feedforward neural networks. As in the former case, this is a constructive algorithm, for which convergence is guaranteed. In the neural tree one distinguishes the structural organization from the functional organization: each neuron of a neural tree receives inputs from, and only from, the input layer; its output does not feed into any other neuron, but is used to propagate down a decision tree. The main advantage of this approach is due to the local processing in restricted portions of input space, during both learning and classification. Moreover, only a small subset of neurons have to be updated during the classification stage. Finally, this approach is easily and efficiently extended to classification in a multiclass problem. Promising numerical results have been obtained on different two- and multiclass problems (parity problem, multiclass nearest-neighbour classification task, etc.) including a ‘real’ low-level speech processing task. In all studied cases results compare favourably with the traditional ‘back propagation’ approach, in particular on learning and classification times as well as on network size.
We study simple, feedforward, neural networks for pattern storage and retrieval, with information theory criteria. Two Hebbian learning rules are considered, with emphasis on sparsely coded patterns. We address the question: under which conditions is the optimal information storage reached in the error-full regime? For the model introduced some time ago by Willshaw, Buneman and Longuet-Higgins, the information stored goes through a maximum, which may be found within the error-less or the error-full regimes according to the value of the coding rate. However, it eventually vanishes as learning goes on and more patterns are stored. For the original Hebb learning rule, where reinforcement occurs whenever both input and output neurons are active, the information stored reaches a stationary value, 1/(π ln 2), when the net is overloaded beyond its threshold for errors. If the coding rate f′ of the output pattern is small enough, the information storage goes through a maximum, which saturates the Gardner bound, 1/(2 ln 2). An interpolation between dense and sparse coding limits is also discussed.
We study an algorithm for a feedforward network which is similar in spirit to the Tiling algorithm recently introduced: the hidden units are added one by one until the network performs the desired task, and convergence is guaranteed. The difference is in the architecture of the network, which is more constrained here. Numerical tests show performances similar to that of the Tiling algorithm, although the total number of couplings in general grows faster.
The authors propose a new algorithm which builds a feedforward layered network in order to learn any Boolean function of N Boolean units. The number of layers and the number of hidden units in each layer are not prescribed in advance: they are outputs of the algorithm. It is an algorithm for growth of the network, which adds layers, and units inside a layer, at will until convergence. The convergence is guaranteed and numerical tests of this strategy look promising.
The authors study the retrieval phase of spin-glass-like neural networks. Considering that the dynamics should depend only on gauge-invariant quantities, they propose that two such parameters, characterising the symmetry of the neural net's connections and the stabilities of the patterns, are responsible for most of the dynamical effects. This is supported by a numerical study of the shape of the basins of attraction for a one-pattern neural network model. The effects of stability and symmetry on the short-time dynamics of this model are studied analytically, and the full dynamics for vanishing symmetry is shown to be exactly solvable.
We study the performance of a neural network of the perceptron type. We isolate two important sets of parameters which render the network fault tolerant (existence of large basins of attraction) in both hetero-associative and auto-associative systems and study the size of the basins of attraction (the maximal allowable noise level still ensuring recognition) for sets of random patterns. The relevance of our results to the perceptron's ability to generalize are pointed out, as is the role of diagonal couplings in the fully connected Hopfield model.
The storage and retrieval of complex sequences, with bifurcation points, for instance, in fully connected networks of formal neurons, is investigated. We present a model which involves the transmission of informations undergoing various delays from all neurons to one neuron, through synaptic connections, possibly of high order. Assuming parallel dynamics, an exact solution is proposed; it allows one to store without errors a number of elementary transitions which are of the order of the number of synaptic connections related to one neuron. A fast-learning algorithm, requiring a single presentation of the prototype sequences, is derived; it guarantees the exact storage of the transitions. It is shown that local learning procedures with repeated presentations, used for pattern storage, can be generalized to sequence storage.
It is possible to construct diluted asymmetric models of neural networks for which the dynamics can be calculated exactly. We test several learning schemes, in particular, models for which the values of the synapses remain bounded and depend on the history. Our analytical results on the relative efficiencies of the various learning schemes are qualitatively similar to the corresponding ones obtained numerically on fully connected symmetric networks.
A model for formal neural networks that learn temporal sequences by selection is proposed on the basis of observations on the acquisition of song by birds, on sequence-detecting neurons, and on allosteric receptors. The model relies on hypothetical elementary devices made up of three neurons, the synaptic triads, which yield short-term modification of synaptic efficacy through heterosynaptic interactions, and on a local Hebbian learning rule. The functional units postulated are mutually inhibiting clusters of synergic neurons and bundles of synapses. Networks formalized on this basis display capacities for passive recognition and for production of temporal sequences that may include repetitions. Introduction of the learning rule leads to the differentiation of sequence-detecting neurons and to the stabilization of ongoing temporal sequences. A network architecture composed of three layers of neuronal clusters is shown to exhibit active recognition and learning of time sequences by selection: the network spontaneously produces prerepresentations that are selected according to their resonance with the input percepts. Predictions of the model are discussed.
We consider a family of models, which generalizes the Hopfield model of neural networks, and can be solved likewise. This family contains palimpsestic schemes, which give memories that behave in a similar way as a working (short-term) memory. The replica method leads to a simple formalism that allows for a detailed comparison between various schemes, and the study of various effects, such as repetitive learning.
One characteristic behaviour of the Hopfield model of neural networks, namely the catastrophic deterioration of the memory due to overloading, is interpreted in simple physical terms. A general formulation allows for an exploration of some basic issues in learning theory. Two learning schemes are constructed, which avoid the overloading deterioration and keep learning and forgetting, with a stationary capacity.
The crossover between invasion percolation (IP) and the Eden model is studied in one-dimensional. Although the mean run length diverges in IP, it converges in the Eden model and for a broad class of perturbations to IP. In addition, IP has anomalous fluctuation effects which are absent in the Eden model. By studying a specific family of models which interpolate between the IP (alpha =0) and Eden (alpha =1/2) limits, we show that the behaviour of the variance crosses over to that found in the Eden model for any alpha >0.
We consider a model of Directed Self-Avoiding Walks (DSAW) on a dilute lattice, using various approaches (Cayley Tree, weak-disorder expansion, Monte-Carlo generation of walks up to 2 000 steps). This simple model appears to contain the essential features of the controversial problem of self-avoiding walks in a random medium. It is shown in particular that with any amount of disorder the mean value for the number of DSAW is different from its most probable value.
We define a family of models to describe cluster growth in random media. These models depend on a temperaturelike parameter and interpolate continuously between the Eden model and the invasion model recently introduced in the study of flow in porous media. Numerical results are presented in two dimensions for a version of these models where growth is biased in a given direction. Directed-invasion clusters are fractal with the same exponents as directed-percolation clusters, but for the other cases studied the clusters are compact. They remain compact even when a "trapping" rule prevents internal holes from being filled.
We study a model of directed compact animals which arises in various fields : partition of an integer, spiralling self avoiding walks, interacting electrons in a strong magnetic field. We give asymptotic formulae for the number of these animals with N sites and length L, and for the mean length < L > at a given N.
The authors study the number A_N of sites that are accessible after N steps at most on clusters at the percolation threshold. On a Cayley tree A_N is of order N^2 if the origin belongs to a larger cluster, whereas its average over all clusters is of order N. This suggests that the intrinsic spreading dimension d, defined by A_N approximately N^d, is equal to two for fractal percolation clusters in space dimensions d >or= 6 and depends on d for d<6. For directed percolation clusters they argue that d is related to usual critical exponents by d=( beta + gamma )/ nu_//. Monte Carlo data that support this relation are presented in two dimensions. Analogous results are derived for lattice animals d=2 on the Cayley tree and d=1/ nu_// for directed animals in any dimensions.
Monte Carlo calculations are performed for two directed systems: the problem of directed animals and the problem of directed aggregation. Taking advantage of recent exact results obtained for the directed animal model, we present a Monte Carlo method which produces directed animals with unbiased statistics, in contrast with previous methods for polymer problems. Large typical clusters of each type are displayed and estimations of the exponents governing the mean length and width of the clusters are obtained, showing that the two models are in different universality classes.
The authors prove a conjecture giving the exact number of directed animals of s sites with any root, on a strip of finite width of a square lattice. The authors also rederive more simply some previous results concerning the connective constant and particular eigenvectors of the transfer matrix.
We study several models of directed animals (branched polymers) on a square lattice. We present a transfer matrix method for calculating the properties of these directed animals when the lattice is a strip of finite width. Using the phenomenological renormalization, we obtain accurate predictions for the connective constants and for the exponents describing the length and the width of large animals (nu_{||} = 9/11 and nu_{orth} = 1/2). For a particular model of site animals, we present and prove some exact results that we discovered numerically concerning the connective constant and the eigenvector of the transfer matrix when the eigenvalue is one. We also propose a conjecture for the number of animals which generalizes the expression guessed by Dhar, Phani and Barma.
Back to menu (top of this page)
Back to menu (top of this page)
Edition of collective volumes
 Jean-Philippe Bouchaud and Jean-Pierre Nadal, Coordinators,
Jean-Philippe Bouchaud and Jean-Pierre Nadal, Coordinators,
From statistical physics to social sciences
Special issue, Compte Rendus de l'Académie des Sciences (CRAS), Physique, Tome 20 fascicule 4, May-June 2019
 .
.
Mathematics and Complexity in Human and Life Sciences,
Special issues of: Mathematical Models and Methods in Applied Sciences (M3AS),
Volume: 19, Issue: supp01, August 2009 (here),
and Volume: 20, Issue: supp01, September 2010 (here).
 proceedings - in English - of a CNRS School - in French - "Economie Cognitive",
Ile de
Porquerolles, Centre IGESA,
25 sept-5 oct 2001.
proceedings - in English - of a CNRS School - in French - "Economie Cognitive",
Ile de
Porquerolles, Centre IGESA,
25 sept-5 oct 2001.
 , 1990.
, 1990.
Back to menu (top of this page)
 L. Bonnasse-Gahot et J.-P. Nadal, "Modéliser les émeutes de 2005 : une vague de violence contagieuse", in L'interdisciplinarité - Voyages au-delà des disciplines, sous la direction de S. Blanc, M. Bouzeghoub et M. Knoop, CNRS Editions, 5 janv. 2023 - ouvrage collectif à l'initiative de la Mission pour les initiatives transverses et interdisciplinaires (MITI) du CNRS.
L. Bonnasse-Gahot et J.-P. Nadal, "Modéliser les émeutes de 2005 : une vague de violence contagieuse", in L'interdisciplinarité - Voyages au-delà des disciplines, sous la direction de S. Blanc, M. Bouzeghoub et M. Knoop, CNRS Editions, 5 janv. 2023 - ouvrage collectif à l'initiative de la Mission pour les initiatives transverses et interdisciplinaires (MITI) du CNRS.

Book
Réseaux de neurones : de la physique à la psychologie
Collection 2ai, Armand Colin 1993 (repris par Dunod/Masson)