


Next: Appendix
Up: Influence of capital
Previous: Simulation results
A comparison of resource depletion for the four models is presented in figure 14.
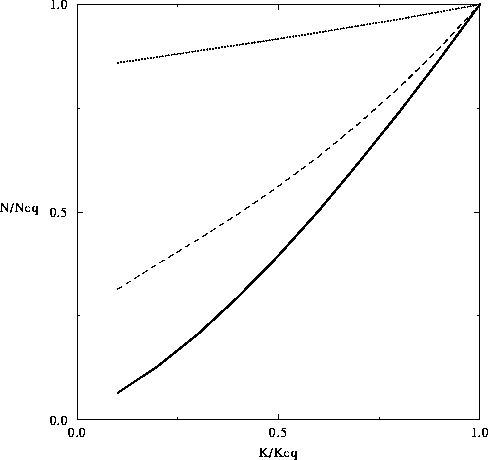
Figure 14: Model comparison: Magnitude of the resource depletion as a function of the distance from equilibrium for each of the four models studied in this paper.
The fraction of initial capital with
respect to equilibrium capital is plotted along the horizontal axis,
and
the fraction of resource at maximum depletion with respect to equilibrium resource along the vertical axis.
Solid line: the basic model of section 2
with 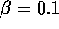 ,
, 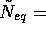
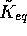 =1; Dots: the model of section 3
with a carrying capacity (
=1; Dots: the model of section 3
with a carrying capacity (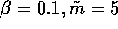 ,
, 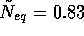 ,
, 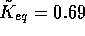 ); Dashes: the price model section 4
(
); Dashes: the price model section 4
(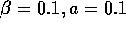 ,
, 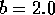 ,
, 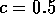 ,
, 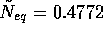 , and
, and 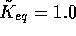 ); Dash dot: the minimum consumption model section 5
(
); Dash dot: the minimum consumption model section 5
(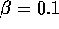 ,
, 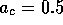 ,
, 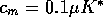 ,
,
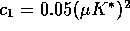 ,
, 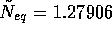 , and
, and 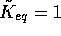 ).
).
The main emphasis of the present paper has been to interpret
resource exhaustion as a dynamical depletion following
an exploitation overshoot due to capital (and labor) inertia.
We have seen that this qualitative result does not seem
to depend upon the degree of simplification of the model since introduction
of a carrying capacity, price dynamics and minimal consumption
does not destroy the observed depletion. Only one
of these features was added at a time in order to simplify algebra
and allow simple interpretation. But extra computer simulations
done with all three features added gave the same qualitative results:
resource depletion is still observed for many parameter choices
although adding up several features often diminish the depletion effect
with respect to equivalent simulations done with only one feature.
Other refinements can still
be introduced, such as endowing agents with more
rational behavior, but we suspect that as long as perfect rationality
is not assumed, oscillations and subsequent depletion
are generic dynamical properties of the dynamics
of the ecological-economical system,
i.e. that they do not depend upon the details of the model.
We will summarize here those results
which should be robust against new refinements of the models,
and which should probably be true also for a number of real systems.
Of course this quest for generic properties still has to be checked
by more modeling and by comparison with data from observations.
We noted in section 2 that other production functions
can be considered and that, in some cases, the equilibrium could
become unstable. But even in those cases the fundamental
result of this study is still valid: exploitation
of renewable resources with open access
yields significant depletion following overshoot when resource
replenishment is fast with respect to capital depreciation.
Previous dynamical models were based
on fast readjustment of effort in proportion to the difference
between cost and benefit [Clark, 1990,Opsomer and Conrad, 1994].
Our model takes into account the fact
that readjustment by capital
variations has a lot of inertia, which is reflected by
the capital depreciation rate.
Of course this inertia is
responsible for the overshoots and depletions. The first
type of fast readjustment of effort would correspond to
some kind of perfect economic rationality, including perfect information,
but human organizations
are more often driven by inertia than by perfect rationality,
which explains our choice for the dynamics of the economic variable.
Let us note here that a limited rationality in capital investment
which would avoid reallocation of capital when profit is small
would not prevent resource depletion because the most profitable
investment is being done when the resource is above its
equilibrium value. When investors would realize that they are loosing
money, capital inertia would prevent fast enough
readjustment of the effort: a readjustment rate fast with respect to
oscillation frequency, which is of order 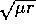 (eq. 13),
would be needed instead of
(eq. 13),
would be needed instead of 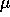 the current adjustment rate of capital. The same qualitative argument
applies to labor readjustments: they could prevent resource depletion
if they would occur faster than
the current adjustment rate of capital. The same qualitative argument
applies to labor readjustments: they could prevent resource depletion
if they would occur faster than 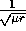 ,
which could only be expected if some other sector of the economy were
growing.
,
which could only be expected if some other sector of the economy were
growing.
We will also discuss in this section some assessment of
various government (or other institutional) intervention tools.
One of the simple results obtained in section 2 is that
the oscillatory character of the dynamics is not changed
by the production coefficients 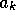 and
and 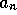 . In other words,
technological and marketing improvement won't save us from overshoots and depletion,
but can increase the level of the renewable resource at equilibrium.
The same conclusion also applies to some management policies such
as shortened seasons and some gear restrictions: they only change
the production coefficients.
. In other words,
technological and marketing improvement won't save us from overshoots and depletion,
but can increase the level of the renewable resource at equilibrium.
The same conclusion also applies to some management policies such
as shortened seasons and some gear restrictions: they only change
the production coefficients.
We have seen that decreasing the capital depreciation rate, 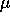 , and thus
, and thus
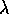 , amplifies the oscillations and level of resource depletion.
In the case where government intervention consists of
supporting investment by providing loans with
low interest rates,
, amplifies the oscillations and level of resource depletion.
In the case where government intervention consists of
supporting investment by providing loans with
low interest rates, 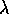 is probably decreased
and the instability increased.
This is one example of a situation where government
support of the industry, or of the fishermen,
could be detrimental to the fish stock,
and thus to the industry in the long term [CEE, 1991].
is probably decreased
and the instability increased.
This is one example of a situation where government
support of the industry, or of the fishermen,
could be detrimental to the fish stock,
and thus to the industry in the long term [CEE, 1991].
We have seen in section 3 that the oscillations and resource
depletion are strongly attenuated when the fishing effort is
such that the harvesting equilibrium is in the neighborhood of
the carrying capacity .
But, of course, the effect is only important
when the fishing effort is small. If the harvesting
equilibrium is far below the carrying capacity, the attenuation
effect is quite reduced and oscillation amplitude is restored.
Market mechanisms and price variations
can reduce resource depletion, but we have seen that this reduction
is limited to a factor of two in the real part of the time constant,
see eqn. 37.
This prediction is made for a rather simple model, however
our assumption that the price decreases inversely proportional
to the production is probably an extreme since it corresponds to
an income that saturates at high productions. We expect instead that prices
drop less rapidly in normal situations,
and thus that the reduction in resource depletion
should be less important than the one predicted in section 4.
The reduction in resource depletion by the market only occurs
when the demand is sufficient to avoid an external support of
prices at production. In this context, institutional
support prevents the reduction of resource depletion
by market mechanisms and might reduce
the ecological sustainability of the system
in the absence of any complementary measure.
Societies have introduced financial mechanisms which allow them
to maintain the personal income of producers even when
natural production is plummeting. The effect of maintaining
a minimum consumption level has been investigated in section 5.
Once more the dynamics shows that the system sustainability is
decreased when a minimum consumption is maintained.
The above results converge in pointing out the fact
that external intervention has to balance the short term
interests of labour and capital with their long term interests
when the renewable resource is in danger of being
depleted.
Acknowledgment
We thank J. Roughgarden for communicating us his preprint
prior to publication and A. T. Charles for a number of useful
comments on the manuscript. The Laboratoire de Physique
Statistique is associated with
CNRS (URA 1306)
,Ecole Normale Supérieure,
and universités Paris 6 et Paris
7 and we acknowledge
financial support from the John D. and Catherine T. Mac Arthur
Foundation, through the New Century Fund, the sponsor of Project 2050, and from the European Science Foundation (Network "Dynamics of Complex Systems in Biosciences").



Next: Appendix
Up: Influence of capital
Previous: Simulation results
weisbuch
Fri Feb 7 13:18:37 GMT+0100 1997

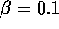 ,
, 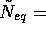
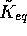 =1; Dots: the model of section 3
with a carrying capacity (
=1; Dots: the model of section 3
with a carrying capacity (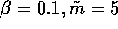 ,
, 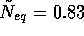 ,
, 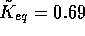 ); Dashes: the price model section 4
(
); Dashes: the price model section 4
(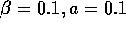 ,
, 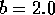 ,
, 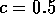 ,
, 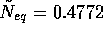 , and
, and 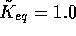 ); Dash dot: the minimum consumption model section 5
(
); Dash dot: the minimum consumption model section 5
(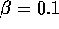 ,
, 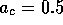 ,
, 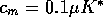 ,
,
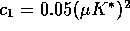 ,
, 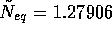 , and
, and 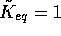 ).
).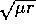 (eq.
(eq. 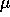 the current adjustment rate of capital. The same qualitative argument
applies to labor readjustments: they could prevent resource depletion
if they would occur faster than
the current adjustment rate of capital. The same qualitative argument
applies to labor readjustments: they could prevent resource depletion
if they would occur faster than 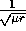 ,
which could only be expected if some other sector of the economy were
growing.
,
which could only be expected if some other sector of the economy were
growing.
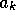 and
and 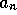 . In other words,
technological and marketing improvement won't save us from overshoots and depletion,
but can increase the level of the renewable resource at equilibrium.
The same conclusion also applies to some management policies such
as shortened seasons and some gear restrictions: they only change
the production coefficients.
. In other words,
technological and marketing improvement won't save us from overshoots and depletion,
but can increase the level of the renewable resource at equilibrium.
The same conclusion also applies to some management policies such
as shortened seasons and some gear restrictions: they only change
the production coefficients.
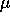 , and thus
, and thus
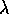 , amplifies the oscillations and level of resource depletion.
In the case where government intervention consists of
supporting investment by providing loans with
low interest rates,
, amplifies the oscillations and level of resource depletion.
In the case where government intervention consists of
supporting investment by providing loans with
low interest rates, 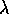 is probably decreased
and the instability increased.
This is one example of a situation where government
support of the industry, or of the fishermen,
could be detrimental to the fish stock,
and thus to the industry in the long term [
is probably decreased
and the instability increased.
This is one example of a situation where government
support of the industry, or of the fishermen,
could be detrimental to the fish stock,
and thus to the industry in the long term [